概率生成函数

由于某种程度上有点闲着没事干所以看了看硬币游戏这个题然后感觉应该学习一下概率生成函数于是就看了看几个题然后似乎发现了什么不得了的科技所以我觉得应该写篇博客总结一下（没错我就不加标点）

首先生成函数的定义不再赘述（其实是不想写）

对了前置知识：同济大学出版社 高等数学 上册 第二章 导数（实际上会求导就行）

1.你看（我旁边爆踩我的joke3579大佬让我起这个名字）

概率生成函数（probability-generating function，PGF）的一般形式：

设离散型随机变量\(x\)的第\(i\)项概率为\(p_i\),那么它的概率生成函数：

\[F(x)=\sum_{i=0}^{\infty}p_ix^i \]

然后是它的一些性质：

\[F(1)=1 \]

\[E(x)=\sum_{i=1}^\infty ip_i=F'(1) \]

可能有人忘了E是个什么东西（比如我看了半天才反应过来），提醒一下这是期望

然后F'(x)就是一阶导（这个都知道吧）

定义\(X\)的方差\(D(x)\)为

\[D(x)=E((x-E(x))^2) \]

（感性理解一下就是把X的所有取值作为每个样本点，E(x)是平均值然后取出来的方差，然后由于X是随机的所以要再取个期望）

那么他就是

\[=E(x^2-2\cdot x\cdot E(x)+E(x)^2) \]

期望的线性性，拆开

\[=E(x^2)-2E(x\cdot E(x))+E(E(x)^2) \]

\(E(x)\)是个常量，可以提出来

\[=E(x^2)-2E(x)^2+E(x)^2 \]

\[=E(x^2)-E(x)^2 \]

后面那个显然是\(F'(1)\)，看前面那个

\[E(x^2)=E(x(x-1)+x) \]

\[=E(x(x-1))+E(x) \]

前面的东西展开成生成函数形式

\[=\sum_{i=0}^\infty i(i-1)p_i=F''(1) \]

于是我们得出了

\[D(x)=F''(1)+F(1)-F'(1)^2 \]

好了结论到此结束。进入我们紧张刺激的应用环节（确信）

P4548 [CTSC2006]歌唱王国

（不要被黑题吓到，这个还是相当像个PGF板子的）

简化题面：给你一个数列，值域为n，长度m，n,m<=1e5,现从1到n等概率选择数生成数列，子串中出现该数列时停止，求期望长度。多组数据，T<=50。

首先我们看题列式子，设\(F(x)\)中\(p_i\)为长度为\(i\)时停止的生成函数，于是互补地，设\(G(x)\)为到\(i\)时没有停止的生成函数。显然我们要求\(F'(1)\)。

于是我们根据题面,，显然的，我们增加一个数字时可能停止也可能没有停止，也就是：

\[xG(x)+1=F(x)+G(x) \]

这个\(G(x)\)还要乘一个\(x\)是表示添加一个数字。因为添加所有数字的概率和为1，所以相当于将所有\(p_i\)往后挪一个。但是这样的话\(p_0\)就没东西了，而且它显然是1，所以加个1（其实加不加没甚影响，但是为了逻辑严谨还是加上吧）

对它两边求导，可得：

\[xG'(x)+G(x)=F'(x)+G'(x) \]

\(x\)代入1，得：

\[G'(1)+G(1)=F'(1)+G'(1) \]

\[G(1)=F'(1) \]

也就是只要求\(G(1)\)。

另一个柿子：

\[G(x)\cdot (\frac 1nx)^m=\sum_{i=1}^ma_iF(x)\cdot (\frac 1nx)^{m-i} \]

其中\(a_i\)当子串1-i为整个数列的一个border时为1，否则为0。

这个的含义也就是将\(G(x)\)这个没有结束的串加上一个名字串显然会结束，但是不一定加完了以后才结束。换句话说，如果这个串的结尾是长度为i的一个border，那么只需要加上剩下的m-i+1长度的串就行了。直观一点，上个（搬来的）图：

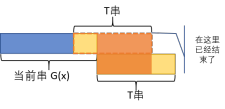
如图所示，橙色部分即为一个border，即只要这个子串是border，那么只需要使剩下的m-i长度的串匹配就行了。而如果使当前的\(G(x)\)补上\(m\)个数字，那么就比结束时的状态\(F(x)\)多了m-i个数字，所以后面要乘回去。

然后尝试化简：
代入\(x=1\)：

\[G(1)\cdot (\frac 1n)^m=\sum_{i=1}^ma_iF(1)\cdot (\frac 1n)^{m-i} \]

把左边的\((\frac 1n)^m\)整到右边并且消掉恒为1的\(F(1)\)：

\[G(1)=\sum_{i=1}^ma_in^i \]

然后就……结束了。显然这个东西可以\(O(m)\)。我用的hash，而且这个题没卡ull。

P3706 [SDOI2017]硬币游戏

简化题面：和上题差不多，就是串是01串，求每个串首次取得的概率。n,m<=300。

首先看有正无穷项考虑生成函数。所以我们设\(F_i(x)\)为第i个串的生成函数，且有：

\[F(x)=\sum_{i=1}^nF_i(x) \]

显然我们要求的是每个\(F_i(1)\)。

然后类似的，设\(G(x)\)为到i长度没有结束的生成函数。所以类似上题，有：

\[xG(x)+1=F(x)+G(x) \]

但是放到这个题似乎并没有什么用的样子，因为我们要求的是每个串的概率，不是期望抛多少次硬币能得到这个串。于是考虑另一个柿子。

但是我们发现，这些东西好像是有点互相影响的。具体地说，当我们考虑在\(G(x)\)后增加一个串\(i\)时，可能会先出现另一个串\(j\)。我们考虑枚举这种关系：

\[G(x)\cdot (\frac 12x)^m=\sum_{j=1}^n\sum_{k=1}^ma_{i,j,k}F_j(x)\cdot (\frac 12x)^{m-k} \]

其中\(a_{i,j,k}\)表示第\(i\)个串的[1,k]与第j个串的[m-k+1,m]相等。我们仍然可以用hash解决这个东西。

然后将\(x\)代入1，得：

\[G(1)=\sum_{j=1}^n\sum_{k=1}^ma_{i,j,k}F_j(1)\cdot 2^k \]

于是我们可以将\(F_i(1)\)和\(G(1)\)进行高斯消元，共n+1个元。由上式可得出n个方程，又有所有的\(F_i(1)\)的和，即\(F(1)=1\)，共n+1个方程。复杂度\(O(n^3)\)。得解。

注意由于k是300的范围，所以\(2^{300}\)要用double存。

提供一下代码吧（虽然我觉得思路差不多了应该就不用代码了，毕竟很短）

/*怎么说呢 我居然才知道double巨大 
所以可以存2^300*/
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int p=2;
unsigned long long hs[310][310],prm[310];
int n,m;
double a[310][310],pw[310],ans[310];
char s[310];
bool cmp(int i,int j,int l,int r,int x,int y){
	return hs[i][r]-hs[i][l-1]*prm[r-l+1]==hs[j][y]-hs[j][x-1]*prm[y-x+1];
}
void gauss(){
    for(int i=1;i<=n;i++){
        int maxx=i;
        for(int j=i+1;j<=n;j++){
            if(fabs(a[j][i])>fabs(a[maxx][i]))maxx=j;
        }
        for(int j=1;j<=n+1;j++)swap(a[i][j],a[maxx][j]);
        for(int j=1;j<=n;j++){
            if(i==j)continue;
            double rate=a[j][i]/a[i][i];
            for(int k=i+1;k<=n+1;k++)a[j][k]-=a[i][k]*rate;
        }
    }
    for(int i=1;i<=n;i++)ans[i]=a[i][n+1]/a[i][i];
}
int main(){
	scanf("%d%d",&n,&m);pw[0]=prm[0]=1;
	for(int i=1;i<=300;i++){
		pw[i]=pw[i-1]*2;
		prm[i]=prm[i-1]*p;
	}
	for(int i=1;i<=n;i++){
		scanf("%s",s+1);
		for(int j=1;j<=m;j++){
			if(s[j]=='H')s[j]=0;
			else s[j]=1;
			hs[i][j]=hs[i][j-1]*p+s[j];
		}
	}
	for(int i=1;i<=n;i++){
		a[i][n+1]=-1;
		for(int j=1;j<=n;j++){
			for(int k=1;k<=m;k++){
				if(cmp(i,j,1,k,m-k+1,m))a[i][j]+=pw[k];
			}
		}
	}
	for(int i=1;i<=n;i++)a[n+1][i]=1;
	a[n+1][n+2]=1;
	n++;gauss();n--;
	for(int i=1;i<=n;i++)printf("%.10lf\n",ans[i]);
}

一些补充：

如评论所示，lyin大佬建议我看两眼BGF求高阶矩。于是我翻了翻具体数学。以下为学习笔记（不一定完全准确，因为我没写过类题不知道正确性怎么样）。然后由于PGF和BGF（双变量生成函数）求矩很像（因为PGF有一个定义就是BGF第一个变量的第\(n\)项的一个分式）而且个人感觉PGF更好看一点，所以直接写PGF了。

首先我们对于一个概率生成函数 \(G(x)\) ，它的 \(m\) 阶累积量 \(\kappa_m\) 由如下的泰勒展开式定义：

\[\ln G(e^x)=\frac{\kappa_1}{1!}x+\frac{\kappa_2}{2!}x^2+\cdots \]

我们通过手算可以得到\(\kappa_1\)就是期望，\(\kappa_2\)就是方差。而由于PGF卷积（两个独立事件的并）可以变成\(\ln\)的加法，所以所有的累积量都具有可加性，也就是线性性。

然后对上边的柿子两边\(\exp\)就可以得到 \(G(x)\) 的 \(m\) 阶矩 \(\mu_m\) ：

\[\begin{aligned} G(e^x)&=\sum_{k=0}P(X=k)e^{kx}\\ &=\sum_{k=0}P(X=k)\sum_{i=0}k^i\frac{x^i}{i!}\\ &=1+\frac{\mu_1}{1!}x+\frac{\mu_2}{2!}x^2+\cdots \end{aligned} \]

显然有

\[\mu_m=P(X=k)k^m=E(X^m) \]

然后我们还有 \(m\) 阶阶乘矩 \(\alpha_m\) 定义如下：

\[\begin{aligned} G(1+x)&=1+\frac{G'(1)}{1!}x+\frac{G''(1)}{2!}x^2+\cdots\\ &=1+\frac{\alpha_1}{1!}x+\frac{\alpha_2}{2!}x^2+\cdots\\ \end{aligned} \]

为什么叫阶乘矩？我们发现

\[G^{(m)}(x)=\sum_{i=0}(X=i)i^{\underline m}x^{i-m}=E(x^{\underline m}) \]

实际上矩和阶乘矩之间转化也是满足普通幂和下降幂之间那一套东西的。直接求一行斯特林数就行了。