数组
1.题目：返回一个整数数组中最大子数组的和。
要求：
输入一个整形数组，数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
2.设计思想：
本题目最大的难点是如何找出子数组并且时间复杂度为O(n)；我的思路是：从总左边（a[0]）开始遍历整个数组，一直到最右边结束（a[n-1]），在这个过程中记录到目前为止最大的子数组和maxsofar。maxsofar初始化成0。假如我们已经找到a[0]到a[n-1]之间的最大子数组和，那么a[0]到a[i]之间的最大子数组和是怎样的呢？要么“还是a[0]到a[i-1]之间的最大子数组和”，要么是“从a[i]开始，往前几个连续的数的最大值”。 在求从a[i]开始，往前几个连续的数的最大值时，用到如下性质：从a[i]开始往前几个连续的数的最大值maxending_i等于(maxending_i-1)+a[i]和0两者之中的最大值，即maxending_i=max((manending_i-1)+a[i],0)
3.源程序代码
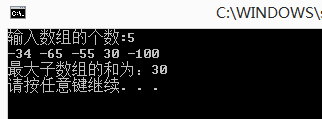
1 //郭婷 信1305 20132916 2015/3/20 2 #include<iostream> 3 #include<time.h> 4 using namespace std; 5 #define max(a,b) ((a)>(b)?(a):(b)) 6 int maxsum(int a[], int n) 7 { 8 int i; 9 int maxsofar = 0; //maxsofar记录到目前为止的的最大值 10 int maxendinghere = 0; //maxendinghere记录从当前位置开始往前几个连续的数的和的最大值 11 for (i = 0; i < n; i++) 12 { 13 maxendinghere = max(maxendinghere + a[i], 0); 14 maxsofar = max(maxsofar, maxendinghere); 15 } 16 return maxsofar; 17 } 18 int main() 19 { 20 int n, i; 21 cout << "输入数组的个数:"; 22 cin >> n; 23 int *a; 24 a = new int[n]; 25 if (a == NULL ) 26 { 27 cout << "Error: memory could not be allocated"; 28 return 1; 29 } 30 srand((unsigned)time(NULL)); 31 for (i = 0; i < n; i++) 32 { 33 a[i] = rand() % 200 - 100; 34 cout << a[i] << " " ; 35 } 36 cout << endl; 37 int max=maxsum(a, n); 38 cout << "最大子数组的和为：" << max << endl; 39 delete[]a; 40 return 0; 41 }
4.总结
刚开始本来打算是找出每一个子数组，再求其最大值，当写程序时发现程序代码比较麻烦，而且好多代码的功能是重复的，于是我就开始阅读上学期的数据结构的课本，找出了适合这个题目的思路。当我写完后，感觉如果刚开始定义了数组的长度，那么这个程序的使用范围就收到限制，于是就思考怎么能使数组的长度可以任意改变，然后我就想到了大一学习C++时讲过的指针可以定义动态数组，于是在该程序中就使用了指针。
