从多项式到 Laurent 级数:Lagrange 反演入门
一、截取与迭代
本文的讨论范围是算法竞赛,讨论的域可以认为是实数域,应用时容易推广得到 NTT 模数域下的结果。
首先要区别 多项式 和 形式幂级数 的概念。本文不太严谨地简称形式幂级数为幂级数。可以粗糙地认为,多项式的次数是有限的,如 \(\sum_{i=0}^{n}a_ix^i\),而幂级数的次数可以是无限的,如 \(\sum_{i=0}^{\infty}b_ix^i\)。多项式是一种特殊的幂级数。
本节主要是讲述一个非常基本的概念:对幂级数的 截取。截取的意思是:只考虑幂级数的前若干位。有时将截取前 \(N\) 位这个操作形式化地写出,就是 \(\bmod x^{N}\)。
根据 Taylor 公式,\(\exp(x)\) 是个关于 \(x\) 的无穷幂级数,多项式 \(\exp\) 指的其实就是求算 \(\exp(F(x))\) 幂级数展开后,前若干项的系数,所以严格来说算的只是 \(\exp(F(x))\) 的截取,也就是求算
很多情况下,我们可以对无穷幂级数进行截取,从而转变成讨论一个多项式问题。
有一些关于多项式的算法是基于倍增的,实际上这些算法倍增的是截取的长度,也就是每次迭代把已知的系数数量翻倍。一般来说,截取长度比所需的更大是没关系的。区别于别的倍增算法,一些多项式倍增算法自身并不对理论复杂度产生 \(\log\) 因子。
接着,介绍一下 和多项式乘法、截取操作对应 的一个逆元概念:多项式乘法逆。对于一个给定的多项式 \(F\),希望求出一个 \(G\) 满足
其中 \(*\) 代表多项式乘法。可以断言,\(F\) 存在乘法逆的充要条件是:常数项非零。
满足这个条件后,从低位到高位考虑,可以一位一位地算出 \(G\) 的系数,即
可以断言,这个乘法逆在模 \(x^{N}\) 意义下是唯一的。多项式乘法满足交换律,所以 \(F\) 的右逆 \(G\) 同时也是 \(F\) 的左逆。
记 \(F\) 的乘法逆,即上面的 \(G\),为 \(F^{-1}\) 或者 \(\frac{1}{F}\)。虽然看起来要说明这个逆是模什么意义下的,但是模 \(x^{N}\) 就是一种截取操作,根据从低位到高位考虑一位一位地算出 \(G\) 的系数的过程,如果记模 \(x^{N}\) 意义下的乘法逆为 \(P\),记模 \(x^{M}\) 意义下的乘法逆为 \(Q\),其中 \(N<M\),那么,\(P\) 实际上就是 \(Q\) 截取前 \(N\) 位。
这种可以从低位到高位一位一位唯一地确定系数的幂级数,我们可以把它自身看成一个无穷的幂级数,而使用时考虑它的截取。
这样,就可以把 \(F^{-1}\) 看作是一个幂级数,满足
我们只需要它的截取。
理解了常数项非零的幂级数的求逆运算会得到一个幂级数后,我们联系一下另一个形式运算中常用的公式:广义二项式展开。
根据广义二项式展开,有
是一个无穷幂级数。这与先前的讨论一致,无非是 \(1-x\) 的乘法逆是一个幂级数。
根据广义二项式展开,还有
是一个无穷幂级数。有一种理解是,这里的幂级数开根,是在反解满足 \(G*G=1-4x\) 的 \(G\)。
不过这里有个问题是,满足 \(G*G=1-4x\) 的 \(G\) 可能 不止一个,而广义二项式展开却 唯一地 写出了一个幂级数,这是否和之前的理论矛盾呢?和非负整数开根同理,\(\sqrt{2}\) 的意义并不是满足 \(a\cdot a=2\) 的唯一解,只是我们为方便,对其中的一个解的标记,具体是哪个解,可以利用正负性进行区分。广义二项式展开 \(\sqrt{1-4x}\) 得到的幂级数,只是对 \(G*G=1-4x\) 其中一个解 \(G\) 的标记,具体是哪个解,我们可以利用广义二项式展开写出来区分。因此这 并不矛盾。
初学者的一个常见的 误解 是:我们可以通过广义二项式展开或者别的公式把任何一个东西写成幂级数。通过一些反例知道这并不正确。
我们可以这样理解幂级数与 \(1/(1-x)\) 或者 \(\sqrt{1-4x}\) 等形式的对应:幂级数的形式运算的结果,与它们的代数运算的结果,具有几乎相同的性质,为了刻画这种性质,而对此作了标记。通过这种标记,我们可以容易地进行形式运算。比如我们借助 \(\sqrt{1-4x}\) 这样的形式,可以容易地知道形式运算下有
如果某个东西通过广义二项式展开或者 Taylor 展开,得到了幂级数,只是因为它本身就是某个幂级数的标记。
通过上述的一些举例,我们大概理解了幂级数的形式运算的逻辑,现在我们可以开始步入本文的正题,关于复合函数的系数的探讨。
现在我们的视野已经从多项式走向了幂级数,通过幂级数,我们可以很方便地写出 递归构造 的结构。
生成函数 理论中,将数列写到一个幂级数的各项系数里,通过幂级数的运算来体现数列的运算。比如说,考虑 \(n\) 个碳原子的烷基的数的生成函数 \(F(x)\),可以根据它的 递归构造 的结构,考虑根下三个子树的形态,这就是一个规模更小但是形式类似的问题,根据 Burnside 引理处理子树同构,得知 \(F(x)\) 满足方程
\(F(x)\) 被 \(F(x)\) 表达,这正是 递归构造 的体现。很多幂级数也有这么一种 递归构造 的结构,我们可以用一个递归形式的方程去写出这种结构,往往这个方程本身又是一个幂级数。
可以根据这样的方程,从低位到高位一位一位的对比左右的系数,从而一位一位地确定 \(F(x)\) 的各项系数。但是这样一位一位确定好像太慢了。为了快速求算这样的幂级数 \(F\) 的前 \(N\) 项,需要引入一个算法:多项式 Newton 迭代。多项式 Newton 迭代是一种 倍增扩大截取长度 的算法,利用它可以求解满足某个方程的幂级数的前 \(N\) 项。形式化地,它可以求解的问题的可以被写成如下模型
\(\texttt{Problem 1.1}\)
\(\phi\) 是某种幂级数。若满足
\[\tag{1.1} \phi(F) \equiv 0 \mod x^N \]的幂级数 \(F\) 是存在且唯一的(或者确定了常数项后就能唯一地确定它),求 \(F\) 模 \(x^N\) 意义下的结果。
这里讨论的 \(\phi\) 是可以用 Taylor 公式写出来的,即
因此可以看出
(注意这里 \(F\) 是一个 形式变元,不加说明时,\(\phi'(F)\) 表达的就是对这个变元 \(F\) 求导。有时候 \(\phi\) 内部会有类似 \(x\) 这样的项,但我们考虑对变元 \(F\) 求导,这里的 \(x\) 就相当于常数性质的东西。)
在上式中取 \(N=1\) 得知 \(F\) 的常数项 \(C\) 满足
一般处理的问题满足这个 \(C\) 的解是好求的。
如果已经求出了 \(F \bmod x^{L+1}\),考虑用它去推出 \(F\bmod x^{2L+1}\)。
这里记 \(G_1=F \bmod x^{L+1},G_2=F\bmod x^{2L+1}\),有
从而
这一步其实就是 扩大截取长度 的关键步骤。注意到
根据上面两式,将上式两边模 \(x^{2L+1}\),注意右式模意义下有值的其实只有两项,\(\phi(G_2)\) 模 \(x^{2L+1}\) 意义下为 \(0\) 当且仅当
如果 \(\phi'(G_1)\) 存在模 \(x^{2L+1}\) 意义下的多项式乘法逆(即常数项不为 \(0\)),就会有
上式就是我们平时使用迭代算法,主要利用的式子。
可以看出主要瓶颈是计算 \(\frac{\phi(G_1)}{\phi'(G_1)}\bmod x^{2L+1}\),计算它的时间一般和 \(L\) 有关,考虑一个增长缓慢的函数 \(f\),Newton 迭代的时间是
所以一般情况下多项式 Newton 迭代自身并不产生 \(\log\) 因子。
\(\square\)
我之前省略了
应该怎么求。主要问题就是如何快速计算模 \(x^N\) 意义下的乘法逆。
我们想要求算 \(F\) 的乘法逆,就得禁用多项式求逆避免循环论证。那么,这个问题真的就不能用迭代算法求算吗?上面还讲过一个更本原的、可以利用的式子 \((1.3)\),根据
简单地变换
同样可以迭代求解,复杂度是 \(O(N\log N)\) 的(这里的 \(\log\) 因子来源于快速多项式乘法)。最后要注意的是,虽然理论上 Newton 迭代自身不产生 \(\log\) 因子,实践中常数因子有可能相对较大。
二、复合与复合逆
幂级数的复合运算的定义是平凡的,和一般的函数的复合运算类似,这里记 \((F\circ G)(x)\) 代表幂级数 \(F(G(x))\)。有时候为了方便也会写作后者即 \(F(G(x))\),注意联系上下文,与用于调整运算顺序的括号、放于右上角代表几阶导的括号区别开。
幂级数的复合运算满足结合律:对于幂级数 \(F,G,H\),有
但是一般来说不满足交换律。对于这种满足结合律的运算,自然会想到去考虑它的逆元。这里的单位元应该定义成一种有恒等性质的东西,对于复合运算来说,这个恒等的幂级数就是 \(H(x)=x\)。因此对于幂级数 \(F\),考虑满足
的幂级数 \(G\)。
现在考虑常数项是否会有限制,我们发现它其实是可能非 \(0\) 的,比如说我们有 \(F(x)=x-1,G(x)=x+1\) 这样的反例。
但是如果规定了常数项为 \(0\) 的话,会带来诸多方便。可以发现对于常数项为零、一次项非零的幂函数 \(F\),\(F^{k}\) 的最低次项就是 \(x^k\),这使得一位一位确定系数时需要考虑的项有限了。
因此,我们只讨论 常数项为零、一次项非零 的幂级数。后文只要涉及幂级数的复合逆,都默认这点。
对于这样的 \(F\),和乘法逆同理,我们通过从低位到高位确定 \(G\) 的系数,就可以唯一地得到这样的的幂级数 \(G\)。
同理考虑另一边,求得满足 \(\hat G\circ F=x\) 的唯一的的 \(\hat G\)。根据复合运算的结合律,就有
因此对于常数项非零的幂级数 \(F\),有唯一的幂级数 \(G\) 是它复合运算下的左逆和右逆,我们称 \(G\) 为 \(F\) 的 复合逆,与乘法逆区分,记作 \(F^{<-1>}\)。根据需求,我们可以考虑这个幂级数的截取。
三、系数的提取
这节内容存在一个非常吊诡的概念:有一种类似幂级数的东西,它的负次项上也有可能有系数,这种级数被称为 形式 Laurent 级数,本文简称 Laurent 级数。要注意和复分析里的 Laurent 级数区分开,尽管它们可能具有某种相似性。
这看起来像是推翻了我们先前的理论,因为我们从来没有考虑过负次项,但实际上它是先前讨论的一种延拓。
Laurent 级数可以被写成
其中 \(n_0\) 是一个指定的整数,满足 \(a_{n_0}\not= 0\),它可以是负数。
(注意这里并不是说我们讨论的 Laurent 级数的 \(n_0\) 都是统一规定的,\(n_0\) 只是指出某个 Laurent 级数的最低次项是谁。)
可以看出:
- \(n_0\ge 0\) 的 Laurent 级数就是先前提到的:幂级数。
- \(n_0=0\) 的 Laurent 级数就是先前提到的:存在乘法逆的幂级数。
- \(n_0=1\) 的 Laurent 级数就是先前提到的:存在复合逆的幂级数。
Laurent 级数的各种形式运算的定义都比较平凡,可以类比形式幂级数。本节讨论的复合函数,其实就是这样的 Laurent 级数的复合。
这里仅介绍它的形式除法的定义。为了把问题转化到我们熟悉的情况,将 \((3.1)\) 改写成
即记成 \(x^{n_0}\) 乘上一个存在乘法逆的 Laurent 级数。
对于 Laurent 级数 \(A,B\),它们的 \(n_0\) 分别是 \(n_a,n_b\),定义 \(A/B\) 是一个 Laurent 级数 \(C\),
其中由于
是两个 \(n_0=0\) 的 Laurent 级数作商,得到了一个 \(n_0=0\) 的 Laurent 级数,这是我们熟悉的结果。这样,\(C\) 就应该是一个 \(n_0=n_a-n_b\) 的 Laurent 级数。
定义了 \(A*B\) 和 \(A/B\),就可以自然地定义 \(A\) 的整数次幂了。
看起来,通过系数平移,很容易将 Laurent 级数转换到平时讨论的幂级数。不过,下面会看到,为什么要大费周折做这么一个延拓。
定义一个 Laurent 级数的 形式留数 为:\(x^{-1}\) 前的系数。那么有
\(\texttt{Lemma 3.1}\)
一个 Laurent 级数在形式求导后,形式留数为 \(0\)。
只需注意到 \(x^{0}\) 的系数在求导后不会传递给 \(x^{-1}\),\(x^{-1}\) 的系数在求导后会传递给 \(x^{-2}\),就可以证明上面的引理了。
\(\square\)
\(\texttt{Lemma 3.2}\)
对于 \(n_0=1\) 的形式 Laurent 级数 \(A(x)\),\(A'(x)A^{k}(x)\) 的形式留数为
\[\tag{3.4} [x^{-1}]A'(x)A^{k}(x)=[k=-1] \]
\(k\not=-1\) 时,考虑对左式逆用形式链式求导(对 \(x\) 求导),得到
根据 \(\texttt{Lemma 3.1}\) 这个是 \(0\)。
\(k=-1\) 时,有(注意根据定义 \(a_1\not=0\))
对于上式中出现的
根据之前的讨论,它的结果正是一个 \(n_0=0\) 并且 \(x^{0}\) 前系数是 \(1\) 的 Laurent 级数。再乘上 \(x^{-1}\),从而 \(A'(x)A^{-1}(x)\) 就是一个 \(n_0=-1\) 并且 \(x^{-1}\) 前系数是 \(1\) 的 Laurent 级数,这就证明了结论。
\(\square\)
\(\texttt{Lemma 3.2}\) 正是考虑形式留数的关键,它给出了一个类似容斥原理中
的式子。我们希望利用这个性质来提取一些信息,下面将利用 \((3.4)\) 证明 Lagrange 反演公式
\(\texttt{Theorem 3.1 }\text{Lagrange Inversion Formula}\)
有 \(n_0=1\) 的 Laurent 级数 \(Q(x)\),则对于整数 \(N,k\),有
\[N\left[x^{N}\right]Q^{k}(x)=k\left[x^{-k}\right](Q^{<-1>}(x))^{-N} \]
根据复合逆的定义
两边取 \(k\) 次方
两边形式求导
注意这里框里的公式代表的是 Laurent 级数 \(Q^k\) 的一阶导 \((Q^{k})'\),在 \(Q^{<-1>}(x)\) 处的取值。
乘 \((Q^{<-1>}(x))^{-N}\) 得到
注意框里 \((\left[w^{i}\right]Q^{k}(w))\) 是一个常数,为了说明这点我将 \(x\) 写成了 \(w\)。
这时在把写到前面的 \((Q^{<-1>}(x))'\) 写到后面,注意到它和 \((Q^{<-1>}(x))^{i-1-N}\) 乘起来是 \((3.4)\) 的形式,这时对两边的形式留数
对于左式框中的式子,根据 \(\texttt{Lemma 3.2}\) 有贡献的只有 \(i=N\),所以就得到了
\(\square\)
根据 \(\texttt{Theorem 3.1}\) 可以推知
\(\texttt{Theorem 3.2 }\text{Lagrange Inversion Formula 2}\)
有 Laurent 级数 \(P(x)\) 和 \(n_0=1\) 的 Laurent 级数 \(Q(x)\),则对于 非零 整数 \(N\),有
\[\left[x^N\right]P(Q(x))=\frac{1}{N}\left[x^{N-1}\right]P'(x)\left(\frac{x}{Q^{<-1>}(x)}\right)^{N} \]
我们只需要确定 \(P(x)=\lambda x^{k}\) 的情况验证,其中 \(\lambda\) 是一个常数。对于一般的 \(P(x)\) 只需枚举 \(k\) 然后求和即可。
这时两边就是
由 \(\texttt{Theorem 3.1}\) 得证。
\(\square\)
这是平时常用的 Lagrange 反演公式,这是因为,其中
只要上下同除以 \(x\),下面就变成了 \(n_0=0\) 的 Laurent 级数,这是一个幂级数。
更近一步,如果 \(P(x)\) 也是幂级数,自然可以放心使用先前的理论,考虑整个幂级数的截取。
只要有办法计算 \(Q(x)\) 的复合逆 \(Q^{<-1>}(x)\),剩下的就是熟悉的多项式操作了。这个复合逆的计算往往就借助先前介绍过的迭代算法。
还有一个被称为另类 Lagrange 反演的公式
\(\texttt{Theorem 3.3 }\text{Lagrange Inversion Formula 3}\)
有 \(n_0=1\) 的 Laurent 级数 \(Q(x)\),则对于整数 \(N,k\),有
\[\left[x^{N}\right]Q^{k}(x)=\left[x^{-k-1}\right](Q^{<-1>}(x))'(Q^{<-1>}(x))^{-N-1} \]
根据复合逆的定义
把左式写开,并两边乘 \((Q^{<-1>}(x))'(Q^{<-1>}(x))^{-N-1}\) 得到
取形式留数并考虑 \(\texttt{Lemma 3.2}\) 得到
\(\square\)
根据 \(\texttt{Theorem 3.3}\) 可以推知我们常用的另类 Lagrange 反演公式
\(\texttt{Theorem 3.4 }\text{Lagrange Inversion Formula 4}\)
有 Laurent 级数 \(P(x)\) 和 \(n_0=1\) 的 Laurent 级数 \(Q\),则对于 整数 \(N\),有
\[\left[x^{N}\right]P(Q(x))=\left[x^{N}\right]P(x)(Q^{<-1>}(x))'\left(\frac{x}{Q^{<-1>}(x)}\right)^{N+1} \]
我们只需要确定 \(P(x)=\lambda x^{k}\) 的情况验证,其中 \(\lambda\) 是一个常数。对于一般的 \(P(x)\) 只需枚举 \(k\) 然后求和即可。
这时两边就是
由 \(\texttt{Theorem 3.3}\) 得证。
\(\square\)
注意这个定理和 \(\texttt{Theorem 3.2}\) 的对比,我们在此可以取 \(N=0\) 来提取 Laurent 级数 \(P(Q(x))\) 的常数项。
由于上面穿插了一些推导性的内容,这里重新将两个常用的 Lagrange 反演公式写在这里
可以在此稍微记忆一下它们,研究它们在算法竞赛中的应用时往往就是直接利用这两条式子的。下文称 \((3.5)\) 为 Lagrange 反演公式,\((3.6)\) 为另类 Lagrange 反演公式。
Lagrange 反演公式的作用,一个是可以求算复合函数的近处系数,即利用迭代算法计算复合逆,另一个是在一些特殊的情况下,用于证明复合函数远处系数的结果。前者的应用往往是套路的,而后者需要强大的洞察力,或者是一些经验。
本节的最后,通过几个例子,展示一些利用 Lagrange 反演的代数技巧和直觉。
\(\texttt{Problem 3.1 }\text{连续多点求值}\)
给定正整数 \(N,R\) 和 \(n_0=1\) 的 Laurent 级数 \(F\),对于每个 \(1\le k\le R\),计算
\[[x^{N}]F^{k}(x) \](source: \(\texttt{ZJOI2020 }\text{抽卡}\))
这是一个比较基本的套路。
看起来需要求很多个位置的答案,我们希望把这些答案放进一个生成函数 \(H\) 中,目标就是求解出这个生成函数。
考虑一个二元生成函数
希望求算的生成函数就是
注意这里 \([x^{N}]G(x,y)\) 的意义是 提取出 一个关于 \(y\) 的 幂级数 \(H(y)\)。这么做的原因是
\(H(y)\) 便是我们的目标。而
这可以看成一个复合函数,其中 \(P(x)=\frac{1}{1-yx},Q(x)=F(x)\)。\(P'(x)\) 显然是可以口算的,并且它每项的形状差不多是 \(x^{i}y^{i+1}\)。如果 \(Q(x)\) 的形状比较好,可以用某种方式计算它的复合逆,提取这样一个复合函数 \(P(Q(x))\) 的系数(得到一个关于 \(y\) 的幂级数 \(H(y)\)),可以 Lagrange 反演(这里看起来是两个元,但我们做的其实只是单元 Lagrange 反演,反演时另一个元的性质相当于常数)。
\(\square\)
\(\texttt{Problem 3.2 }\text{口算复合逆}\)
(I)
给定一个元素 \(\ge 2\) 的正整数的集合 \(D\),求算满足方程
\[F(x)=x+\sum\limits_{i\in D}F^i(x) \]并且常数项为 \(0\) 的幂级数 \(F\) 的第 \(N\) 次项的系数。
(source: \(\text{大朋友和多叉树}\))
(II)
给定正整数 \(k_1,k_2\),求算满足方程
\[F(x)=x(1+F^{k_1}(x)+F^{k_2}(x)) \]并且常数项为 \(0\) 的幂级数 \(F\) 的第 \(N\) 次项的系数。
(source: \(\texttt{LG 7592 }\text{数树}\))
我们发现这两个方程都有一种 递归构造 的结构。
解决这类问题的直觉是,先看出 \(F\) 是 \(n_0=1\) 的 Laurent 级数,然后通过一些移项操作使得等式的某一边只剩下 \(x\),另一边是某个函数复合 \(F\),从而口算出 \(F\) 的复合逆 \(F^{<-1>}\)。
(I)
可以看出 \(F\) 其实是一个 \(n_0=1\) 的 Laurent 级数。口算出它的复合逆
于是就可以用 Lagrange 反演 \(O(N\log N)\) 提取出 \(F\) 的单项系数。
(II)
可以看出 \(F\) 其实是一个 \(n_0=1\) 的 Laurent 级数。口算出它的复合逆
于是就可以用 Lagrange 反演提取出 \(F\) 的单项系数,但注意到主要是算
的单项系数,通过一点分析可以做到 \(O(N)\)。
\(\square\)
\(\texttt{Problem 3.3 }\text{提取常数项}\)
给定正整数 \(v,k\),求算幂级数
\[\left(\frac{1-x^v}{x(1-x)}\right)^{k} \]的常数项。
(source: \(\texttt{LG 7445 }\text{线段树}\))
解决这个问题的直觉是,令 \(F(x)=\frac{1-x^v}{x(1-x)}\),这是一个 \(n_0=-1\) 的 Laurent 级数,因此我们考虑 \(F^{-1}\),得到一个 \(n_0=1\) 的 Laurent 级数 \(Q(x)=\frac{x(1-x)}{1-x^v}\)。
令 \(P(x)=x^{-k}\),于是由另类 Lagrange 反演公式
迭代算法计算 \(Q\) 的复合逆即可。
\(\square\)
\(\texttt{Problem 3.4 }\text{口算远处系数}\)
求
\[\frac{1}{\sqrt{1-4x}}\left(\frac{1-\sqrt{1-4x}}{2x}\right)^{m} \]的 \(n\) 次项系数。
(source: \(\texttt{《具体数学》}\)、\(\texttt{SDOI2019 }\text{小孩召开法}\))
原文里这个恒等式是用广义二项式级数写出的。这里摘原文的一句话:广义二项式级数的特殊情形 \(t=2\) 和 \(t=-1\) 特别重要,因为它们的系数一而再、再而三地在 递归构造 的问题中出现。
解决这个问题的直觉来源于,考虑 \(n_0=1\) 的 Laurent 级数(可以二项式展开验证一下)
它满足方程(这个方程被称为二叉树方程,可以考虑一下它的组合意义)
于是
于是原式就可以写成一个比较漂亮的复合形式
而我们根据 \((3.8)\) 可以轻易地知道 \(F(x)\) 的复合逆是
因此,可以考虑用 Lagrange 反演求算它的第 \(n\) 项系数。后面的工作比较简单,可以参考 EntropyIncreaser 的 这篇文章。答案是
\(\square\)
\(\texttt{Problem 3.5 }\text{反算数列的封闭形式}\)
还没编好。
\(\texttt{Problem 3.6 }\text{转整式递推}\)
还没编好,感觉是一个转整式递推的套路。
https://xyix.github.io/posts/?&tags=lagrange-inversion&postname=luogu-7896
(source: \(\texttt{LG7896 }\text{Moke 的游戏}\))
后记
关于形式 Laurent 级数的教程似乎很难在国内搜索引擎中查到,如果需要查找完整的介绍可以在 Wikipedia 里查看词条 Formal power series 下面的 Formal Laurent series。
由于个人习惯以及不确定有些做法是谁先发明的,懒得写 Reference 了,这里一并表示感谢。

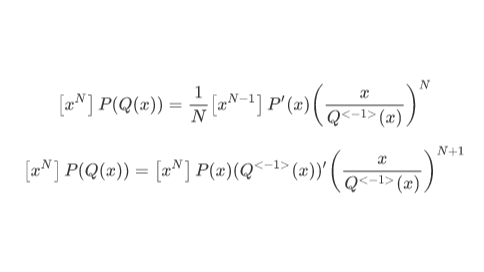 当我们的视角移向了负次项。
当我们的视角移向了负次项。

