Travelling DP

【问题描述】
山山很喜欢旅行,他坐飞机的次数也非常非常多,所以他成为了空中司机航空公司的会
员,并且有一张白金会员卡。
山山规划了接下来一段时间的行程,他需要坐飞机 n 次,现在空中司机给了他 m 种
优惠政策。
对于第 i 种政策,山山可以花费 ci 元办理一张“Ti 日通飞证”,这样他就可以 在某
个连续的 T i 天内坐飞机不花钱。对于每个政策,山山可以办理很多张这样的通飞证。山山
也可以每次直接购买机票,因为他是白金会员,他只需要花费 k 元就可购得一张机票。
由于山山还只是一名小学生,他的计算能力不是很强,于是他希望你能帮他算出完成行
程所需的最小花费。

【输入格式】
输入文件名为 travelling.in。
第一行为三个正整数 n m k。
第二行为 n 个正整数 a1 ~ an ,表示接下来的 n 次坐飞机分别在 a1 ~ an 天后。
保证这个数列递增且不重复。
接下来 m 行每行两个整数 Ti ci ,表示每种优惠政策中的 T 和 c 值。

【输出格式】
输出文件名为 travelling.out。
输出仅一行一个整数 ans 表示答案。

【样例输入与输出】
travelling.in 3 2 4
1 3 4
2 7
3 8

travelling.out
11

【数据范围与约定】
对于 20%的数据:0 < n <= 1000
对于 50%的数据:0 < n <= 10000
对于 100%的数据:0 < n <= 500000,0 <= m <= 20,0 < k, ci <= 1000,0 < ai<= 10 9 ,0 < ti <= 10 9

---

 

首先最无脑的DP是可以直接写出来的：

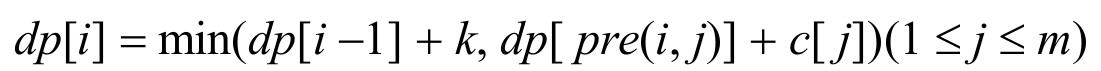
但是这样做的复杂度为O（nmti），很有可能超时（只有50分）。

所以我们就来优化这个方程。

首先nm的复杂度是肯定优化不下去的，那么我们就考虑怎么O（1）求pre[i][j]，pre[i][j]记录第i天用第j种方案必须交钱的最早天。

可以直接预处理pre[i][j]。

我们知道每次坐飞机的时间是递增的，那么对于每一个pre[i][j],随着i的递增，pre[i][j]也是递增的（每次坐飞机用j方案必须交钱最早的那天一定是递增的，因为每次坐飞机的时间是递增的）。

那么我们就可以O（nm）预处理后，

再用O（nm）DP，就可以得到答案了。

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

#define ll long long
#define il inline
#define double

#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))

using namespace std;

il int gi()
{
	int x=0,y=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
		{
			if(ch=='-')
				y=-1;
			ch=getchar();
		}
	while(ch>='0'&&ch<='9')
		{
			x=x*10+ch-'0';
			ch=getchar();
		}
	return x*y;
}

int f[500045];

int day[500045];

int pre[500045][22];

struct ce
{
	int days,mon;
}c[45];

int main()
{
	freopen("travelling.in","r",stdin);
	freopen("travelling.out","w",stdout);
	
	memset(f,127/3,sizeof(f));

	int n=gi(),m=gi(),k=gi();

	for(int i=1;i<=n;i++)
		day[i]=gi();

	for(int i=1;i<=m;i++)
		c[i].days=gi(),c[i].mon=gi();
	
	for(int j=1;j<=m;j++)//init
		{
			int l=1;
			for(int i=1;i<=n;i++)
				{
					while(c[j].days&&l<i)
						l++;
					pre[i][j]=l-1;
				}
		}

	f[0]=0;
	for(int i=1;i<=n;i++)
		{
			f[i]=min(f[i],f[i-1]+k);
			for(int j=1;j<=m;j++)
				f[i]=min(f[i],f[pre[i][j]]+c[j].mon);//DP
		}

	printf("%d\n",f[n]);

	return 0;
}