wows 线段树+差分
【问题描述】
山山最近在玩一款游戏叫战舰世界(steam 游戏太少了),他被大舰巨炮的魅力折服,于
是山山开了一局游戏,这次发现目标是一艘战列舰新墨西哥级,舰桥很高,原本应该打在目
标身后的圆形水域内的炮弹,都打在了舰桥上,于是落点变成了一条直线。
因为新墨西哥中间高两边低,所以按概率算,炮弹命中数中间多,两边少,并且中央区
域容易穿透出现高伤害,所以 山山向中间发射的炮弹比两边多,因为他有强迫症,所以一
个位置炮弹发射数相对于上一个位置的数目的变化量为 ki(整体大概构成一个山峰状),新墨
西哥操纵者因为 OI 的时候玩游戏,脑袋被教练按键盘了,所以站着不动,导致山山能够百
发百中,求数轮齐射后,在一段区域的命中数为阶梯增长的长度 (阶梯增长为 A+0K,
A+1K· · ·K 随意取,单调增)
(为了便于统计伤害,我们把新墨西哥分成 n 段,同时也
便于瞄准。
新墨西哥被教练抓着脑袋摁键盘了,我就不信我也 gbhghuyjhhfdhsfdhndxf......
【输入格式】
输入文件名为 wows.in。
第一行 n m, 表示新墨西哥被分成 n 段, 山山开炮数和询问命中次数的总数,
第二行以后每行开头一个 f,0 表示开炮,1 表示询问
如果开炮 后面还有 5 个参数 l,r,a,k,p
表示 山山向 l 到 r 段开炮,l 段开了 a 炮,以后 l + 1 到 p 段分别开 a+k,a+k+k,
a+k+k+k·
·
·炮, p+1 到 r 段开 a+(p-l-1)k、a+(p-l-2)k··
·炮
如果询问 后面有 l,r 表示询问区域(保证任意相邻区段数据之差在任何时候在 int 内)
【输出格式】
输出文件名为 wows.out。
对于每个询问输出一个数,表示符合要求的最大长度,后跟一个回车

【数据范围与约定】
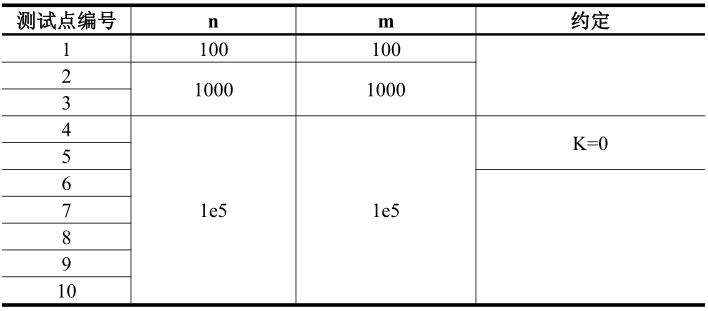
这题是这次考试中最难的,我本来还欣喜地打了三十分的暴力,但是是世态炎凉,一个点都没捞到。。。
接下来是正解(来自我们谭巨佬的思想和方法):
首先我们要理解题意,他每次让我们修改两段区间,然后在线询问我们区间中最长等差长度。
恩。。。
可以知道很变态,现在我们来慢慢把题目变简单。
因为每次问的是相邻区间的差,所以我们将计就计,用一个差分数组c[i]保存a[i+1]-a[i]。
这样简化了之后,假如我们拿到第一组样例,就会这样(这是第一次):
num 2 3 4 5 6
c 2 2 -2 -2 -2
这样理解了后,我们就要考虑怎么优化这个差分数组,可以在时限内解决问题。
现在,每次询问其实就是问在范围内最长的相同的差分数组。
于是我们用线段树来维护这个值。
每个线段树节点维护:
ls,rs:区间最左右边连续相同的长度。
lp,rp:区间最左右边连续相同的数字。
s:区间最长连续相等区间(目标)。
合并区间时:
c[rt].ls=c[rt<<1].ls,c[rt].rs=c[(rt<<1)+1].rs;
c[rt].lp=c[rt<<1].lp,c[rt].rp=c[(rt<<1)+1].rp;
c[rt].s=max(c[rt<<1].s,c[(rt<<1)+1].s);
然后是一些细节:
当左边区间的差分数组都相等,并且右边区间最左边的数和左边区间最右边的数相等,那么我们就可以直接把右边区间最左边长度加到新区间上。
反之亦然。
然后是两个区间对s的影响:
如果左边区间最右边数字和右边区间最左边数字相等,那么就可以合并。
所以有:
c[rt].s=max(c[rt].s,c[rt<<1].rs+c[(rt<<1)+1].ls);
另外,这种线段树和平时写的线段树不一样,
在修改和查询的时候,必须要当前区间全部包括才能修改和查询,所以会有不一样。
代码:
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#define ll long long
#define il inline
#define db double
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
il int gi()
{
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
y=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*y;
}
struct node
{
int ls,rs;
int lp,rp;
int s;
int l,r;
}c[4000045];
int lazy[4000045];
il node merge(node L,node R)//he bing liang ge jie dian,fan hui yi ge jie dian
{
node tmp;
int mid=L.r;
tmp.l=L.l;
tmp.r=R.r;
tmp.ls=L.ls;
tmp.rs=R.rs;
tmp.lp=L.lp;
tmp.rp=R.rp;
if(L.rs==L.r-L.l+1&&L.rp==R.lp)
tmp.ls+=R.ls;//xi jie 1
if(R.ls==R.r-R.l+1&&R.lp==L.rp)
tmp.rs+=L.rs;
tmp.s=max(L.s,R.s);
if(L.rp==R.lp)
tmp.s=max(tmp.s,L.rs+R.ls);
return tmp;
}
void build(int rt,int l,int r)
{
if(l>r)
return;
if(l==r)
{
c[rt].l=c[rt].r=l;
c[rt].ls=c[rt].rs=1;
c[rt].lp=c[rt].rp=0;
c[rt].s=1;
return;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build((rt<<1)+1,mid+1,r);
c[rt]=merge(c[rt<<1],c[(rt<<1)+1]);
}
void pushdown(int rt)
{
if(lazy[rt])
{
lazy[rt<<1]+=lazy[rt];
lazy[(rt<<1)+1]+=lazy[rt];
c[rt<<1].lp+=lazy[rt];
c[rt<<1].rp+=lazy[rt];
c[(rt<<1)+1].lp+=lazy[rt];
c[(rt<<1)+1].rp+=lazy[rt];
lazy[rt]=0;
}
else
return;
}
void add(int rt,int l,int r,int L,int R,int num)
{
if(l>r)
return;
if(l==L&&r==R)
{
c[rt].lp+=num;
c[rt].rp+=num;
lazy[rt]+=num;
return;
}
int mid=(l+r)>>1;
pushdown(rt);
//xi mian de xiu gai bi xu quan bu bao han,suo yi bu yi yang
if(L>mid)
add((rt<<1)+1,mid+1,r,L,R,num);
else if(R<=mid)
add(rt<<1,l,mid,L,R,num);
else
{
add(rt<<1,l,mid,L,mid,num);
add((rt<<1)+1,mid+1,r,mid+1,R,num);
}
c[rt]=merge(c[rt<<1],c[(rt<<1)+1]);
}
node query(int rt,int l,int r,int L,int R)
{
if(L==l&&R==r)
return c[rt];
int mid=(l+r)>>1;
pushdown(rt);
c[rt]=merge(c[rt<<1],c[(rt<<1)+1]);
//he xiu gai yi yang
if(L>mid)
return query((rt<<1)+1,mid+1,r,L,R);
else if(R<=mid)
return query(rt<<1,l,mid,L,R);
else
{
node r1=query(rt<<1,l,mid,L,mid);
node r2=query((rt<<1)+1,mid+1,r,mid+1,R);
return merge(r1,r2);
}
}
int main()
{
freopen("wows.in","r",stdin);
freopen("wows.out","w",stdout);
int n=gi(),m=gi();
build(1,1,n-1);
int l,r,a,k,p,H;
for(int i=1;i<=m;i++)
{
H=gi();
if(H==0)
{
l=gi(),r=gi(),a=gi(),k=gi(),p=gi();
if(l!=1)
add(1,1,n-1,l-1,l-1,a);
if(l<=p-1)
add(1,1,n-1,l,p-1,k);
if(p<=r-1)
add(1,1,n-1,p,r-1,-k);
if(r!=n)
add(1,1,n-1,r,r,-a-(2*p-l-r)*k);
}
else
{
l=gi(),r=gi();
if(l==r)
printf("1\n");
else
printf("%d\n",query(1,1,n-1,l,r-1).s+1);
}
}
return 0;
}


