Java异或详解
一、异或介绍
异或是一种基于二进制的位运算,用符号XOR或者 ^ 表示,其运算法则是对运算符两侧数的每一个二进制位,同值取0,异值取1。
性质
1、交换律
2、结合律(即(a^b)^c == a^(b^c))
3、对于任何数x,都有x^x=0,x^0=x
4、自反性 A XOR B XOR B = A XOR 0 = A
二、异或使用
异或运算最常见于多项式除法,不过它最重要的性质还是自反性:A ^ B ^ B = A,即对给定的数A,用同样的运算因子(B)作两次异或运算后仍得到A本身。
例如,所有的程序教科书都会向初学者指出,要交换两个变量的值,必须要引入一个中间变量。但如果使用异或,就可以节约一个变量的存储空间: 设有A,B两个变量,存储的值分别为a,b,则以下三行表达式将互换他们的值 表达式 (值) :
A = A ^ B B = B ^ A A = A ^ B
例:
int a = 10, b = 5;
a = a ^ b;
b = a ^ b;
a = a ^ b;
类似地,该运算还可以应用在加密,数据传输,校验等等许多领域。
三、应用举例
问题:1-1000放在含有1001个元素的数组中,只有唯一的一个元素值重复,其它均只出现一次。每个数组元素只能访问一次,设计一个算法,将它找出来;不用辅助存储空间,能否设计一个算法实现?
解法一:显然已经有人提出了一个比较精彩的解法,将所有数加起来,减去1+2+...+1000的和。这个算法已经足够完美了,相信出题者的标准答案也就是这个算法,唯一的问题是,如果数列过大,则可能会导致溢出。
解法二:异或就没有这个问题,并且性能更好。将所有的数全部异或,得到的结果与1^2^3^...^1000的结果进行异或,得到的结果就是重复数。
但是这个算法虽然很简单,但证明起来并不是一件容易的事情。这与异或运算的几个特性有关系。首先是异或运算满足交换律、结合律。 所以,1^2^...^n^...^n^...^1000,无论这两个n出现在什么位置,都可以转换成为1^2^...^1000^(n^n)的形式。 其次,对于任何数x,都有x^x=0,x^0=x。 所以1^2^...^n^...^n^...^1000 = 1^2^...^1000^(n^n)= 1^2^...^1000^0 = 1^2^...^1000(即序列中除了n的所有数的异或)。 令,1^2^...^1000(序列中不包含n)的结果为T 则1^2^...^1000(序列中包含n)的结果就是T^n。 T^(T^n)=n。 所以,将所有的数全部异或,得到的结果与1^2^3^...^1000的结果进行异或,得到的结果就是重复数。 当然有人会说,1+2+...+1000的结果有高斯定律可以快速计算,但实际上1^2^...^1000的结果也是有规律的,算法比高斯定律还该简单的多。
google面试题的变形:一个数组存放若干整数,一个数出现奇数次,其余数均出现偶数次,找出这个出现奇数次的数?
解法有很多,但是最好的和上面一样,就是把所有数异或,最后结果就是要找的,原理同上!!代码如下:
public void fun() {
int a[] = { 22, 38,38, 22,22, 4, 4, 11, 11 };
int temp = 0;
for (int i = 0; i < a.length; i++) {
temp ^= a[i];
}
System.out.println(temp);
}
四、交换两个数的三种方法
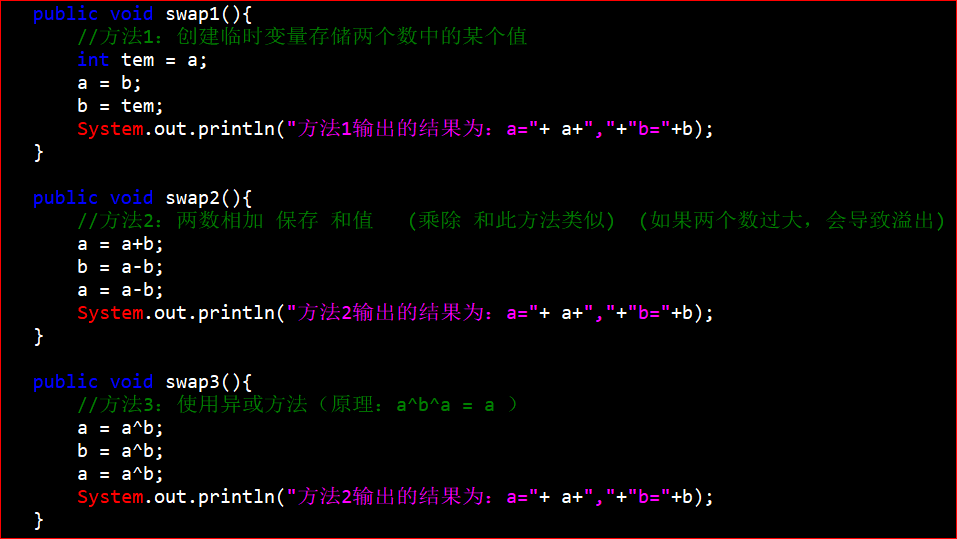
int a=5,b=10; a=a+b; //a=15,b=10 b=a-b; //a=15,b=5 a=a-b; //a=10,b=5
但是这样做有一个缺陷,假设它运行在vc6环境中,那么int的大小是4 Bytes,所以int变量所存放的最大值是2^31-1即2147483647,如果我们令a的值为2147483000,b的值为1000000000,那么a和b相加就越界了。
事实上,从实际的运行统计上看,我们发现要交换的两个变量,是同号的概率很大,而且,他们之间相减,越界的情况也很少,因此我们可以把上面的加减法互换,这样使得程序出错的概率减少:
int a=5,b=10; a -= b; //a=-5,b=10 b += a; //b=5,a=-5 a = b - a; //a=10,b=5
通过以上运算,a和b中的值就进行了交换。表面上看起来很简单,但是不容易想到,尤其是在习惯引入第三变量的算法之后。
它的原理是:把a、b看做数轴上的点,围绕两点间的距离来进行计算。
具体过程:第一句“a-=b”求出ab两点的距离,并且将其保存在a中;第二句“b+=a”求出a到原点的距离(b到原点的距离与ab两点距离之差),并且将其保存在b中;第三句“a+=b”求出b到原点的距离(a到原点距离与ab两点距离之和),并且将其保存在a中。完成交换。
参考文献: https://www.cnblogs.com/JhSonD/p/6374397.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号