递归:如何用三行代码找到“最终推荐人”?
一、什么是递归?
数据结构和算法有两个难点,一个是递归,一个是动态规划。
方法或函数调用自身的方式称为递归调用,调用称为递,返回称为归。
举例: 以在电影院看电影为例,如果你想知道你前面有多少排,于是你问前面一排的人,前面一排的人再继续问前面一排的人。
其中
代表你想知道你自己在哪一排,
表示你前面一排的人想知道自己是哪一排。因此可以轻松的写出如下递归代码:
int f(int n){
if (n == 1){
return 1;
}
return f(n-1) + 1;
}
二、什么样的问题可以用递归解决呢?
一个问题只要同时满足以下3个条件,就可以用递归来解决,写递归代码最关键的是写出递归公式,寻找终止条件。:
1、问题的解可以分解为几个子问题的解。何为子问题?就是数据规模更小的问题。
2、问题与子问题,除了数据规模不同,求解思路完全一样
3、存在递归终止条件
举例:
在该问题中,可以分解为,我当前走了x台阶后,剩下的n-x台阶该怎么走这种子问题,其求解思路还是一样的,所以递归公式我们已经找到了,剩下的就是寻找终止条件。
当我们走到最后的时候,剩下一个台阶或者两个台阶。剩下一个台阶只有一种走法,剩下两个台阶有两种走法,等价于剩下零个台阶有一种走法。所以终止条件为
static int f(int n){
if (n == 1 || n == 0){
return 1;
}
return f(n-1) + f(n-2);}
三、递归代码要警惕堆栈溢出
因为递归是不停的调用该方法,而在Java虚拟机中,每使用一个方法就会在虚拟机栈中添加一个栈帧,如果一直添加,就可能会出现堆栈溢出的问题。我们可以通过在代码中限制递归调用的最大深度来解决这个问题。例如上面的台阶问题。
static int depth = 0;
static int f(int n){
depth ++;
if (depth > 1000) throw excption;
if (n == 1 || n == 0){
return 1;
}
return f(n-1) + f(n-2);}
但是这种做法不能够完全解决问题,最大允许的递归深度与当前线程中栈的剩余空间大小有关系,无法事先计算。如果实时计算就会增加代码复杂度影响可读性。
四、递归代码要警惕重复计算
还是台阶案例,将整个递归分解下如图:
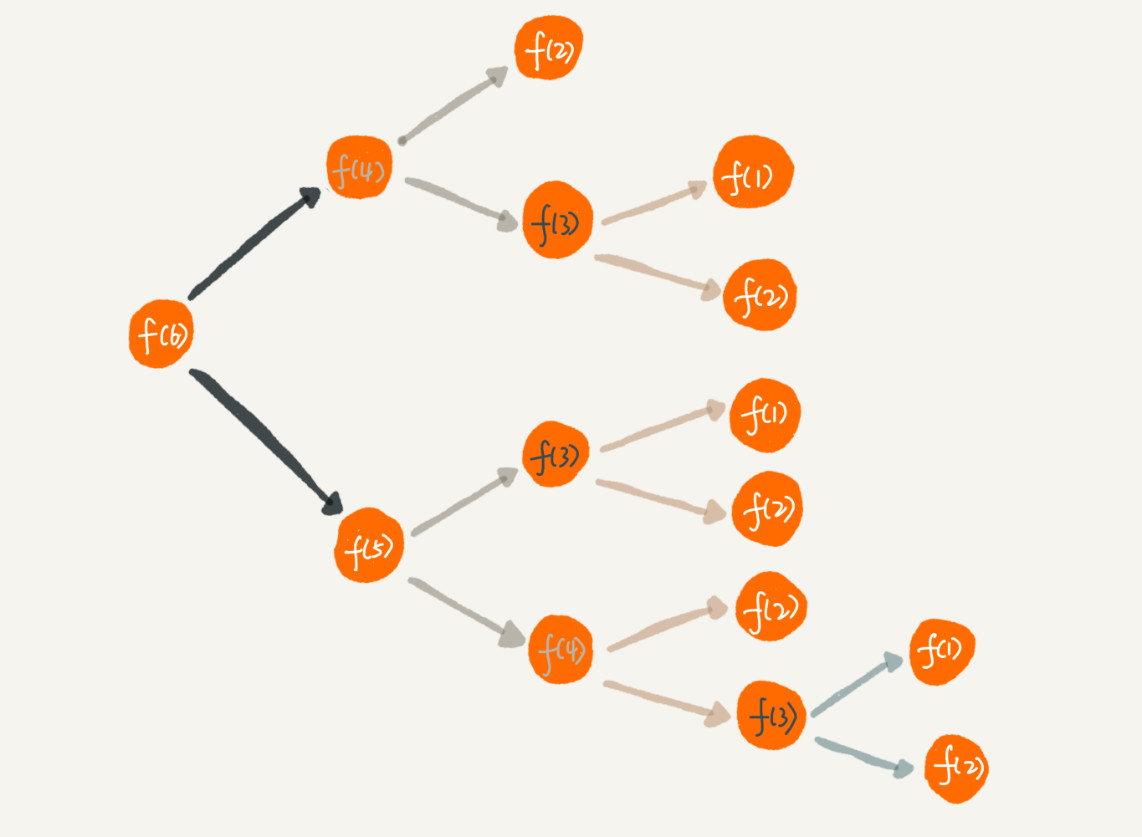
从图中,我们可以直观地看到,想要计算 f(5),需要先计算 f(4) 和 f(3),而计算 f(4) 还需要计算 f(3),因此,f(3) 就被计算了很多次,这就是重复计算问题。
为了避免重复计算,我们可以通过一个数据结构(比如散列表)来保存已经求解过的 f(k)。当递归调用到 f(k) 时,先看下是否已经求解过了。如果是,则直接从散列表中取值返回,不需要重复计算,这样就能避免刚讲的问题了。
public int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
// hasSolvedList可以理解成一个Map,key是n,value是f(n)
if (hasSolvedList.containsKey(n)) {
return hasSolvedList.get(n);
}
int ret = f(n-1) + f(n-2);
hasSolvedList.put(n, ret);
return ret;
}
五、怎么将递归代码改写为非递归代码?
递归有利有弊,利是递归代码的表达力很强,写起来非常简洁;而弊就是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题。
改写电影院的例子:
int f(int n) {
int ret = 1;
for (int i = 2; i <= n; ++i) {
ret = ret + 1;
}
return ret;
}
同样,台阶的例子也可以改为非递归的实现方式。
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
int ret = 0;
int pre = 2;
int prepre = 1;
for (int i = 3; i <= n; ++i) {
ret = pre + prepre;
prepre = pre;
pre = ret;
}
return ret;
}
六、解答开篇
推荐注册返佣金的这个功能我想你应该不陌生吧?现在很多 App 都有这个功能。这个功能中,用户 A 推荐用户 B 来注册,用户 B 又推荐了用户 C 来注册。我们可以说,用户 C 的“最终推荐人”为用户 A,用户 B 的“最终推荐人”也为用户 A,而用户 A 没有“最终推荐人”。
一般来说,我们会通过数据库来记录这种推荐关系。在数据库表中,我们可以记录两行数据,其中 actor_id 表示用户 id,referrer_id 表示推荐人 id。
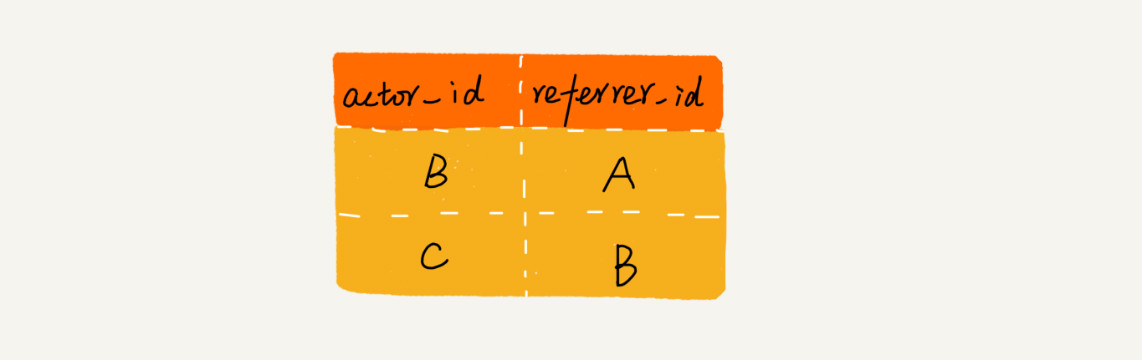
基于这个背景,我的问题是,给定一个用户 ID,如何查找这个用户的“最终推荐人”?解决方案如下:
long findRootReferrerId(long actorId) {
Long referrerId = select referrer_id from [table] where actor_id = actorId;
if (referrerId == null) return actorId;
return findRootReferrerId(referrerId);
}
七、调试递归方案
1、打印日志发现,递归值。
2、结合条件断点进行调试。


