约瑟夫问题
1、什么是约瑟夫问题
约瑟夫是犹太军队的一个将军，在反抗罗马的起义中，他所率领的军队被击溃，只剩下残余的部队40余人，他们都是宁死不屈的人，所以不愿投降做叛徒。一群人表决说要死，所以用一种策略来先后杀死所有人。于是约瑟夫建议：每次由其他两人一起杀死一个人，而被杀的人的先后顺序是由抽签决定的，约瑟夫有预谋地抽到了最后一签，在杀了除了他和剩余那个人之外的最后一人，他劝服了另外一个没死的人投降了罗马。
约瑟夫问题是个著名的问题：N个人围成一圈，第一个人从1开始报数，报M的将被杀掉， 下一个人接着从1开始报。如此反复，最后剩下一个，求最后的胜利者。 例如只有三个人，把他们叫做A、B、C，他们围成一圈，从A开始报数，假设报2的人被杀掉。 首先A开始报数，他报1。侥幸逃过一劫。 然后轮到B报数，他报2。非常惨，他被杀了 C接着从1开始报数 接着轮到A报数，他报2。也被杀死了。 最终胜利者是C
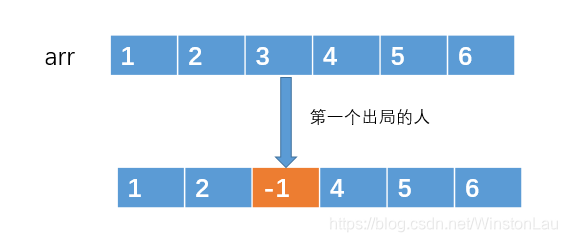
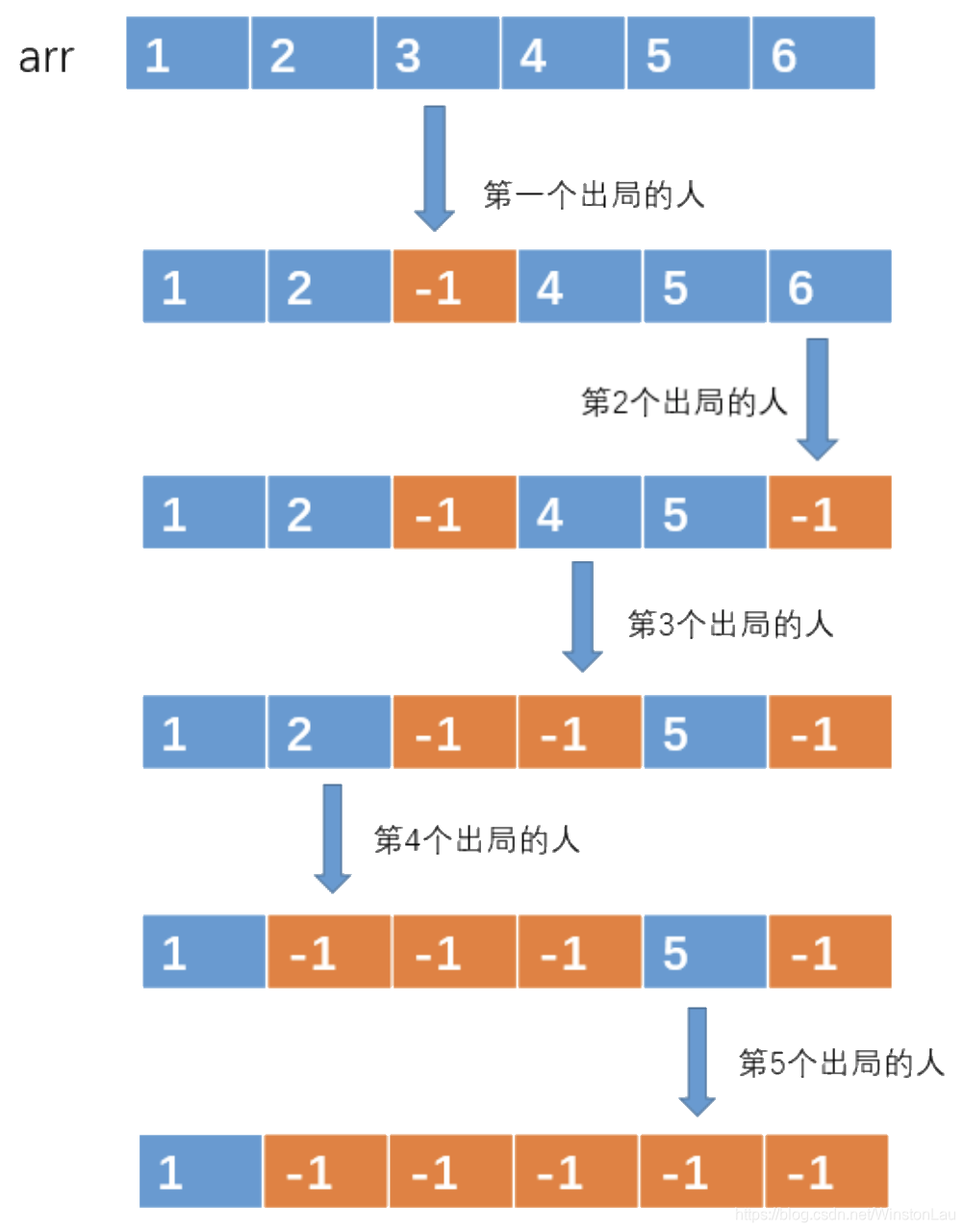
2、用数组解决
- 用数组来解决，应该是很多第一次接触到这个问题的人最容易想到的一种方式，思想很简单，但实现起来需要考虑的地方还是很多的
-
用一个数组来存放 1，2，3 … n 这 n 个编号（假设 n = 6, m = 3，k = 1）
-
然后不停着遍历数组，对于被选中的编号，我们就做一个标记，例如编号 arr[2] = 3 被选中了，那么我们可以做一个标记，例如让 arr[2] = -1，来表示 arr[2] 存放的编号已经出局了
-
然后就按照这种方法，不停着遍历数组，不停着做标记，直到数组中只有一个元素是非 -1 的，这样，剩下的那个元素就是我们要找的元素了。演示如下
-
编码实现这里就不写了，本文的重点在第三种方法
-
这种做法的时间复杂度是 O(nm), 空间复杂度是 O(n)
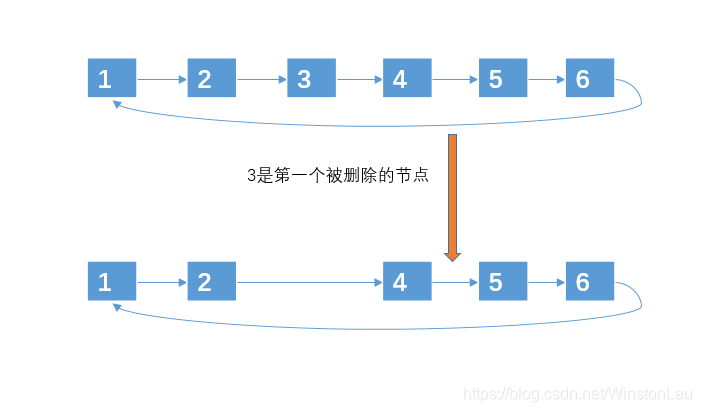
3、用环形链表解决
-
用链表来处理其实和上面处理的思路差不多，只是用链表来处理的时候，对于被选中的编号，不再是做标记，而是直接移除，因为从链表移除一个元素的时间复杂度很低，为 O(1)
-
当然，上面数组的方法你也可以采用移除的方式，不过数组移除的时间复杂度为 O(n)
-
先创建一个环形链表来存放元素
-
然后在遍历链表的同时做删除操作，这里就不全部演示了
-
核心代码如下：
// 定义链表节点 class Node{ int date; Node next; public Node(int date) { this.date = date; } } public static int solve(int n, int m) { if(m == 1 || n < 2) return n; // 创建环形链表 Node head = createLinkedList(n); // 遍历删除 int count = 1; Node cur = head; Node pre = null;//前驱节点 while (head.next != head) { // 删除节点 if (count == m) { count = 1; pre.next = cur.next; cur = pre.next; } else { count++; pre = cur; cur = cur.next; } } return head.date; } static Node createLinkedList(int n) { Node head = new Node(1); Node next = head; for (int i = 2; i <= n; i++) { Node tmp = new Node(i); next.next = tmp; next = next.next; } // 头尾串联 next.next = head; return head; } -
这种做法的时间复杂度是 O(nm), 空间复杂度是 O(n)，和第一种方法一样。
-
缺点：要模拟整个游戏过程，时间复杂度高达O(nm)，当n，m非常大(例如上百万，上千万)的时候，几乎是没有办法在短时间内出结果的。
4、用递归公式解决
约瑟夫环是一个经典的数学问题，我们不难发现这样的依次报数，似乎有规律可循。为了方便导出递推式，我们重新定义一下题目。
问题： N个人编号为1，2，……，N，依次报数，每报到M时，杀掉那个人，求最后胜利者的编号。先抛结论，然后在分析。
下面我们不用字母表示每一个人，而用数字。
1、2、3、4、5、6、7、8、9、10、11 表示11个人，他们先排成一排，假设每报到3的人被杀掉。
刚开始时，头一个人编号是1，从他开始报数，第一轮被杀掉的是编号3的人。
编号4的人从1开始重新报数，这时候我们可以认为编号4这个人是队伍的头。第二轮被杀掉的是编号6的人。
编号7的人开始重新报数，这时候我们可以认为编号7这个人是队伍的头。第三轮被杀掉的是编号9的人。
……
第九轮时，编号2的人开始重新报数，这时候我们可以认为编号2这个人是队伍的头。这轮被杀掉的是编号8的人。
下一个人还是编号为2的人，他从1开始报数，不幸的是他在这轮被杀掉了。
最后的胜利者是编号为7的人。
下图表示这一过程
现在再来看我们递推公式是怎么得到的！
代码如下：
int cir(int n,int m){
int p=0;
for(int i=2;i<=n;i++){
p=(p+m)%i;
}
return p+1;
}
