2023年题解总和

合集 - 复盘游记题解(14)

1.2023NOIP游记2023-11-24 2.2023CSP复赛游寄2023-11-24 3.2023CSP初赛游祭2023-11-24 4.AtCoder Beginner Contest 复盘合集2023-12-28 5.USACO 2023-2024 赛季复盘2023-12-17 6.2024年题目选讲2024-01-06 7.2023CSP复赛/NOIP备战模拟赛复盘集合2023-11-24 8.2023CSP初赛备战复盘合集2023-11-24 9.2023.7信友队暑假集训第2次测试复盘2023-11-24 10.2023暑假信友队集训游记2023-11-24

11.2023年题解总和2024-01-07

12.2023 年终总结2024-01-05 13.洛谷9月月赛翻盘记2023-11-24 14.CodeForces 比赛复盘集合2023-12-17

洛谷P3161 [CQOI2012] 模拟工厂题解

P3161[CQOI2012]模拟工厂题解。题目

其实发现这是一道状压，发现这道题是一道数学题，其实就很简单了。对于每一次的订单我们可以设：

$t i m e$ 为距离下一个订单的时间。
$n u m$ 为这个订单要生产的数量。
$x$ 为生产能力。
$y$ 的时间可以用来提高工厂的生产力。那我们就可以得出公式： $(x + y) \times (t i m e - y) = n u m$

整理后：（~~一元二次方程应该都会对吧。~~） $y^{2} + (x - t i m e) \times y - x \times t i m e + n u m$

一个一元二次方程肯定要判根啊，如果有实数根那么就是有解。所以我们只需要对方程判根，有根那么这个订单就可以完成。

如果有实数根只需要解这个方程即可： $\frac{t i m e - x + \sqrt{(x - t i m e)^{2} - 4 \times x \times t i m e - 4 \times n u m}}{2}$

程序首先先枚举每一个状态：状压！毕竟 $n \leq 15$ 。然后就去计算每一个订单，进行计算，判断可行性，对可行的方案取 $max$ 即可。AC code：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
struct node{
	ll t,g,m;
}a[25],st[25];
ll n;
bool cmp(node a,node b){
	return a.t < b.t;
}
ll jisuan(ll x,ll time,ll y){
	ll a = 1;
	ll b = x-time;
	ll c = y-x*time;
	ll delta = b*b-4*a*c;
	if(delta>=0)return (ll)((-b+sqrt(delta)) / 2 / a);
	return -1;
}
ll ans;
void run(ll zy){
	ll t = 0;
	ll sum =0;
	for(int i = 1;i <= n;i++){
		if(zy & (1<<(i-1))) {
			st[++t] = a[i];
			sum += a[i].m;
		}
	}
	
	ll m=1;
	ll sheng=0;
	
	for(ll i = 1;i <= t;i++){
		ll mt = st[i].t - st[i-1].t;
		//最多提高生产力的时间
		ll num=0;//所有产品累计
		for(ll j =i;j<=t;j++){
			num += st[j].g;
			if(num > sheng){
				mt = min(mt,jisuan(m,st[j].t-st[i-1].t,num-sheng));
			}
		}
		if(mt == -1) return ;
		m += mt;
		sheng += m * (st[i].t-st[i-1].t-mt) - st[i].g;
	}
	ans = max(ans,sum);
}	
int main(){
	cin >> n;
	for(ll i = 1;i <= n;i++){
		cin >> a[i].t >> a[i].g >> a[i].m;
	}
	sort(a+1,a+1+n,cmp);
	for(ll i = 0;i < (1<<n);i++){
		run(i);//状压，2^n枚举所有订单可能性
	}
	cout << ans;
	return 0;
}

~~给蒟蒻的第一篇题解点个赞呗~~
广告
 算了，还不如来这里

洛谷 P6239 [JXOI2012] 奇怪的道路题解

P6239 [JXOI2012] 奇怪的道路

首先，拿到题面， $n \leq 30$ ， $k \leq 8$ ，~~这不就暴搜吗~~。再想想，紫题会给你暴搜的机会吗？所以进一步思考，发现这其实是一道 DP，而且数据这么小，肯定是给状压 DP 的样子。

经过一定思考，发现我们可以直接线性枚举 $[1, n]$ 。

为什么呢？因为每一个点只能和前 $k$ 个点连边，而且每一个点只能有偶数条连边。那么我们枚举到 $i$ ，它可以改变的点最前面是 $i - k$ ，它下一个就是 $i + 1$ ，那么枚举到 $i + 1$ 时肯定没办法再改变 $i - k$ ，所以，到了 $i$ 是改变 $i - k$ 最后一次机会，所以再此时必须改变 $i - k$ 变成偶数。

于是，我们可以设计 dp 状态 $d p_{i, j, l, z}$ 代表枚举点数 $i$ ，枚举边 $j$ ，前 $k$ 个点中的第 $l$ 个， $z$ 为状态压缩，代表着每一个点的奇偶性。

因此我们可以推出转移方程（见代码）。

注意事项：状压 DP 用到位运算，因为位运算的优先级复杂，建议勤快的加括号，~~我就是因为这个括号的问题调了很久~~。

AC CODE:

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,k;
int dp[40][40][20][550];
const int p=1e9+7;
//定义：dp[i][j][l][z]
//表示枚举到第i个点，第j条边，z为i个点与前k个点的状压连边状态，已经连了l条边
signed main(){
	cin >> n >> m >> k;
	dp[2][0][0][0]=1;
	for(int i = 2;i <= n;i++){
		//枚举每一个点
		for(int j = 0 ;j <= m;j++){	
			//枚举每一条边
			for(int z=0;z<(1<<(k+1));z++){
				//枚举状态
				for(int l = 0;l <= k;l++){
					//枚举已经连的边数
					if(l!=min(i-1,k)){
						dp[i][j][l+1][z]=(dp[i][j][l+1][z] + dp[i][j][l][z])%p;
						dp[i][j+1][l][z^(1<<(l+k-min(k,i-1)))^(1<<k)] = (dp[i][j+1][l][z^(1<<(l+k-min(k,i-1)))^(1<<k)] + dp[i][j][l][z]) % p;
					}
					if(l==min(i-1,k) && !(z & 1))
						dp[i+1][j][0][z>>1]=(dp[i+1][j][0][z>>1]+dp[i][j][l][z])%p;
					
				}
			}
		}
	}
	cout<<dp[n+1][m][0][0] % p;
	return 0;
}

洛谷 P4872 OIer们的东方梦题解

前言

一个下午，一个晚上，一个早上，可以算是一天了吧，终于调出了这道题，纪念一下吧！！！

食用更佳。

这道题其实就是一道简简单单的 BFS 模（du）板（liu）题。

说难不难，简单不简单，虽然没有难的算法，但是就是码量一百多行，比较难调。

题目难度绿，思维难度橙，代码难度蓝。真是个~~绝世好题~~。

题目意思

就是一个最短路问题，开个优先队列跑 BFS。有很多种路，需要逐个 if 判断过去。

为了后面讲解，我们设置一个 id 代表拿的太阳花或者剑的状态（具体见代码）。

如果你逐个查找每个传送门会卡成 $O (N^{4})$ 。如果我们要去间隙传送门，那么必然是为了一次性传送，或者传去其他地方拿个太阳花或者剑之类的。所以这样暴力的算法就会使其有可能会从这个传送门跳到另一个传送门，然后什么东西也没拿就跳回又另一个传送门。然后我们会发现因为你每次到的都是 step 最小的点，所以只要你有一次跳到了这个点传送门，那么在当前的 id 下乱跳间隙的 step 是最优的，所以代码中再开一个 vis2 数组来表示 id 下是否记录了这些传送门的点。因为 id 最多是 $3$ ，是个小常数，可以忽略，因此复杂度降到 $O (N^{2})$ 。

注意事项

本题有很多细节需要注意。

BFS 开始 vis 数组没有初始化起点（一般人应该也不会有这个问题）~~但我经常这样~~。
X、S、E在判断的时候是相当于空地的，是可以直接走过的，不要忽略。
重载函数别写错了。

本人犯的最大错误

因为整个程序都是依靠着优先队列实现最优解的保持，但是由于本人结构体重载函数学的不好，所以把符号写反了 ~~（尽管嘲讽~~。

接下来讲一下结构体重载函数的写法。

struct data{
	int x,y;
}a[N];

以上是一个结构体标准写法。如果我们想对 a 排序，按照 x 从小到大排序，那么我们可以写一个 cmp 函数。

bool cmp(data a,data b) {
	return a.x<b.x;
}

但是优先队列等无法写自定义函数的时候，就得用到结构体重载函数，就是在结构体内部定义函数。下面介绍其中一种写法。

struct data{
	int x,y;
   friend bool operator<(const struct data &a,const struct data &b){
		return a.step > b.step;
	}
}a[N];

反正 friend 开头那一行就背下来就好了，~~虽然我不知道为什么~~。就是觉 C++ 创始人很奇怪，这还要加 const，struct…… 注意了，还要加取地址符。

感觉很奇怪！

然后函数里的内容就要跟 cmp 写法基本一样了，但是重点是：他的符号跟 cmp 是反的！，所以从小到大排序要用大于符号！~~（我就挂在这了）~~。

最后，附上 AC code：~~（注释齐全，自认马蜂良好，容易理解）~~。

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define endl "\n"
using namespace std;
const int N = 1005;
int n,m;
string c[N];
int vis[N][N][3],vis2[3];
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
struct node{
	int x,y,step;
	bool sun;//是否遇到过太阳花
	bool jian;//是否有楼观剑
	friend bool operator<(const struct node &a,const struct node &b){
		return a.step > b.step;
	}
};
struct data{
	int x,y;
}s[N*N];int si;
int bx,by,ex,ey;//设置起点和终点
bool check(int x,int y){//判断边界情况
	if(x<1||x>n||y<1||y>m)return true;
	return false;
}
int getid(node x){
	if(x.jian) return 2;
	if(x.sun) return 1;
	return 0;
}
int main(){
	memset(vis,0x3f,sizeof vis);
	cin >> n >> m;
	for(int i = 1;i <= n;i++){
		cin >> c[i];
		c[i]=' '+c[i];
	}
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= m;j++){
			if(c[i][j]=='M')c[i][j]='0';//麻薯都说吃了没用，还不如不吃！
			else if(c[i][j]=='S')bx=i,by=j,c[i][j]='0';
			else if(c[i][j]=='E')ex=i,ey=j,c[i][j]='0';
			else if(c[i][j]=='X')s[++si].x=i,s[si].y=j;
		}
	}
	priority_queue<node> q;
	vis[bx][by][0]=0;
	q.push({bx,by,0,0,0});
//	cout<<bx<<" "<<by<<endl;
	while(!q.empty()){
		node f=q.top();
		q.pop();
//		cout<<f.x << " "<< f.y<<endl;
		if(f.x==ex && f.y==ey) {
			cout<<f.step;
			return 0;
		}
		int nowid = getid(f);
		for(int i = 0 ;i < 4;i++){
			int xx=f.x + dx[i];
			int yy=f.y + dy[i];
			if(check(xx,yy)) continue;
			if(c[xx][yy] == '0' || c[xx][yy]=='X'){//是空地
				if(vis[xx][yy][nowid] > f.step+1){//如果比最短路径短，那么就走
					vis[xx][yy][nowid] = f.step+1;
					q.push({xx,yy,f.step+1,f.sun,f.jian});
				}
			}else if(c[xx][yy]=='1'){//是墙
				if(f.jian){//有jian才能走
					if(vis[xx][yy][nowid] > f.step+1){
						vis[xx][yy][nowid] = f.step+1;
						q.push({xx,yy,f.step+1,f.sun,f.jian});
					}	
				}
			}else if(c[xx][yy]=='2'){//是little 妖怪
				if(f.jian||f.sun){//有剑或太阳花，把你斩了
					if(vis[xx][yy][nowid] > f.step+1){
						vis[xx][yy][nowid] = f.step+1;
						q.push({xx,yy,f.step+1,f.sun,f.jian});
					}	
				}else{//没剑，花3s把你干了，再加上1s移动时间
					if(vis[xx][yy][nowid] > f.step+4){
						vis[xx][yy][nowid] = f.step+4;
						q.push({xx,yy,f.step+4,f.sun,f.jian});
					}						
				}		
			}else if(c[xx][yy]=='3'){//big 妖怪
				if(f.jian||f.sun){//有剑或太阳花，把你斩了
					if(vis[xx][yy][nowid] > f.step+1){
						vis[xx][yy][nowid] = f.step+1;
						q.push({xx,yy,f.step+1,f.sun,f.jian});
					}	
				}else{//没剑，花8s把你干了，再加上1s移动时间
					if(vis[xx][yy][nowid] > f.step+9){
						vis[xx][yy][nowid] = f.step+9;
						q.push({xx,yy,f.step+9,f.sun,f.jian});
					}						
				}		
			}else if(c[xx][yy]=='4'){//太阳花
				if(vis[xx][yy][max(1,nowid)] > f.step+1){
					vis[xx][yy][max(1,nowid)] = f.step+1;
					q.push({xx,yy,f.step+1,1,f.jian});
				}
			}else if(c[xx][yy]=='5'){//是jian
				if(vis[xx][yy][2] > f.step+1){
					vis[xx][yy][2] = f.step+1;
					q.push({xx,yy,f.step+1,f.sun,f.jian});
				}
				if(vis[xx][yy][nowid] > f.step+6){
					vis[xx][yy][nowid] = f.step+6;
					q.push({xx,yy,f.step+6,f.sun,1});
				}								
			}
		}
		int xx=f.x,yy=f.y;
		if(c[xx][yy]=='X'){
			if(vis2[getid(f)])continue;vis2[getid(f)]=1;
			for(int i = 1;i <= si;i++){
				if(s[i].x==xx&&s[i].y==yy) continue;
				if(vis[s[i].x][s[i].y][nowid] > f.step+1){
					vis[s[i].x][s[i].y][nowid] = f.step+1;
					q.push({s[i].x,s[i].y,f.step+1,f.sun,f.jian});
				}					
			}
		}
	}
	cout<<"We want to live in the TouHou World forever";
	return 0;
}

广告。

AT_abc324_e [ABC324E] Joint Two Strings 题解

题目大意

给你 $n$ 个字符串 $s$ ，和一个字符串 $t$ 。

问你，有多少组是 $s_{j}$ 拼在 $s_{i}$ 后面所组成的新字符串中， $t$ 是其子序列。

思路

分析： $5 \times 10^{5}$ 的数据肯定需要 $O (n)$ 或 $O (n \log n)$ 的时间复杂度过掉， $\log n$ 很容易想到应该是二分，于是我们就往二分的思路去想。

首先先进行预处理：

我们可以遍历 $n$ 个 $s$ 。我们可以开两个数组：

$f$ 数组， $f_{i}$ 记录的是每一个 $s_{i}$ 的最长前缀
$b$ 数组， $b_{i}$ 记录的是每一个 $s_{i}$ 的最长后缀

当什么情况两个字符串拼起来的新字符串， $t$ 可以是它们的子序列呢？

如果前面的字符串的最长前缀 $+$ 后面的字符串的最长后缀的长度大于等于 $t$ 的长度，那么我们就可以拼出一个子序列。

于是，我们可以枚举前面的字符串，然后二分出最长后缀大于等于 $n$ 减去这个字符串的最长前缀的个数。那么就是这个字符串后面可以接着的字符串的个数，然后对答案 $a n s$ 加上这个数。

因此我们就完成这一题了。

最后的提醒：十年 OI 一场空，不开 long long 见祖宗

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5+5;
int n;
string t,s[N];
int f[N],b[N]; // 前缀和后缀数组
signed main(){
	cin >> n >> t;
	for(int i = 1 ;i <= n;i++)
		cin >> s[i];
	for(int i = 1;i <= n;i++){
		for(int j = 0 ;j < s[i].size();j++)
			if(s[i][j] == t[f[i]])
				f[i]++;//计算si的最大前缀
		for(int j = s[i].size()-1;j >= 0;j--)
			if(s[i][j] == t[t.size()-1-b[i]])
				b[i]++;//计算si的最大后缀
	}
	int m = t.size();
	sort(f+1,f+1+n);sort(b+1,b+1+n);//排序以便二分
	int ans=0;
	for(int i = 1;i <= n;i++) ans+= n-(lower_bound(b+1,b+1+n,m-f[i])-b)+1;//进行二分的操作，计算以si为前面的字符串，后面有多少种可能
	cout<<ans;
	return 0;
}

AC链接

[ABC327D] Good Tuple Problem 题解

分析：

这一道题很容易发现可以用并查集来维护 ~~（不知道为什么其他人都用了图论）~~， $a_{i}$ 与其对应的 $b_{i}$ 代表着 $a_{i}$ 这个集合里不能存在着 $b_{i}$ 。

根据只有存在两个集合，所以我们会发现，若 $x$ 与 $y$ 不在一个集合且 $x$ 与 $z$ 也不在一个集合，那么 $x$ 和 $y$ 就在一个集合内。然后针对可以在一个集合内的点进行并查集。到最后再判断一下每一个点 $a_{i}$ 是否与 $b_{i}$ 不在一个集合内，若不在，合法，否则不合法。

时间复杂度大概在 $O (n)$ 左右，可以过去。

code。

[ABC328D] Take ABC 题解

题目大意：

给你一个字符串 $s$ 。你要在其中找到多少个 ABC 的子串，例如 AABCBC 算两个，删掉中间的 ABC 后，前面的和后面的加起来也是一个 ABC，所以就算两个。

思路分析：

首先很容易写出暴力，把一个 ABC 提取出来后把后面的元素往前移，然后再重复操作，但是我们发现时间复杂度会卡成 $O (n^{2})$ 。 $n$ 指 $s$ 的长度。

于是我们想到用栈来维护，遍历这个字符串，把每一个字符串扔进栈里，设栈顶为 $b k$ ，如果栈中 $b k - 2$ 的位置为 A， $b k - 1$ 的位置为 B， $b k$ 的位置为 C，那么就是可以组成一个 ABC。这样遍历的时候每一次做一下判断，如果发现存在 ABC，那么就把这对应的栈中位置给删除了即可。

link。

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define fir first
#define se second
#define endl '\n'
#define debug puts("AK IOI")
using namespace std;
const int N = 2E5+5;
char st[N];int bk,n;
string s;
int main(){
	cin >> s;
	n=s.size();
	s=' '+s;
	for(int i = 1;i <= n;i++){
		st[++bk]=s[i];
		if(bk >= 3 && st[bk-2]=='A' && st[bk-1]=='B' && st[bk]=='C'){
			bk-=3;
		}
	}
	for(int i = 1;i <= bk;i++) cout<<st[i];
	
	return 0;
}

[ABC328C] Consecutive 题解

给一个长度为 $n$ 的字符串 $s$ ， $q$ 次询问，每一次 $l$ 和 $r$ 区间内有多少个 $s_{i}$ 等于 $s_{i - 1}$ 。

$10^{5}$ 的数据 $O (N^{2})$ 暴力肯定行不通。于是我们考虑预处理前缀和，处理到 $i$ 下标以及之前有多少个 $s_{i}$ 等于 $s_{i - 1}$ 。

每一次查询 $O (1)$ 回答。注意要减去的边界是 $q z h_{l}$ ，因为 $q z h_{l}$ 其实是包含着 $s_{l}$ 与 $s_{l - 1}$ 的贡献。所以这个不能算入这个区间的贡献中。因此前缀和的公式应该是 $q z h_{r} - q z h_{l}$ 。

link。

[ABC329D] Election Quick Report 题解

题目翻译

有一场选举，要从 $N$ 名候选人中选出一名获胜者，候选人编号为 $1, 2, \dots, N$ ，共有 $M$ 张选票。

每张选票正好投给一位候选人，其中 $i$ 票投给了候选人 $A_{i}$ 。

选票将按照从第一张到最后一张的顺序进行统计，每张选票统计完毕后，将更新并显示当前的获胜者。

得票最多的候选人即为获胜者。如果有多个候选人得票最多，则候选人编号最小者为获胜者。

对于每个 $i = 1, 2, \dots, M$ ，如果只计算前 $i$ 张选票，则确定获胜者。

分析

每次操作我们只需要对之前的最大值进行比较，如果比他还大，那么更新最大值。因为我们要知道是哪一个人的，所以用一个 pair 来存储其对应的下标。

比较方式是如果大于，则替换；如果等于且下标小于（小于等于），也替换。

AC code：

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define fir first
#define se second
#define endl '\n'
#define debug puts("AK IOI")
using namespace std;
const int N = 2e5+5;
int a[N];
int n,m;
pair<int,int> maxn;
int vis[N];
int main(){
	cin >> n >> m;
	for(int i = 1;i <= m;i++){
		scanf("%d",&a[i]);
		vis[a[i]]++;
		if(vis[a[i]] > maxn.first || (vis[a[i]]==maxn.first && a[i] < maxn.second)){
			maxn.first = vis[a[i]];
			maxn.second = a[i];
		}cout<<maxn.second<<endl;
	}
	return 0;
}

[ABC329C] Count xxx 题解

插曲

因为本人看错了题面，买看到一个子串只包含一种字母，所以切完 D 和 E 才回来发现很简单。

问题翻译

给你一个长度为 $N$ 的字符串 $S$ ，由小写英文字母组成。

求 $S$ 的非空子串中有多少个是一个字符的重复。在这里，作为字符串的两个子串是相等的，即使它们是以不同的方式得到的，也不加以区分。

$S$ 的非空子串是通过删除 $S$ 开头的零个或多个字符和结尾的零个或多个字符得到的长度至少为一个的字符串。例如，ab 和 abc 是 abc 的非空子串，而 ac 和空字符串则不是。

分析

如果有一个字符串 AAABAA，那么 AA 和 A 这个子串会重复计算过。所以我们只需要计算每一个字符最长的连续长度。

于是我们可以开一个 $a n s$ 数组，然后维护这每一个字符的最长连续长度，最终答案就是 $a n s$ 数组中的和即可。

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define fir first
#define se second
#define endl '\n'
#define debug puts("AK IOI")
using namespace std;
int n;
string s;
int ans[30];
int main(){
	cin >> n >> s;
	s=' '+s;
	int res=0;
	for(int i = 1;i <= n;i++){
		if(s[i] != s[i-1]){
			res=0;
		}res++;
		ans[s[i]-'a'] = max(ans[s[i]-'a'],res);
	}
	int cnt=0;
	for(int i=0;i <=26;i++){
		cnt+=ans[i];
	}cout<<cnt;
	return 0;
}

AT_abc329_e [ABC329E] Stamp 题解

题目翻译

给你两个字符串： $S$ 由大写英文字母组成，长度为 $N$ ； $T$ 也由大写英文字母组成，长度为 $M$ ，小于 $N$ 。有一个长度为 $N$ 的字符串 $X$ ，它只由 # 字符组成。请判断是否有可能通过执行以下任意次数的操作使 $X$ 与 $S$ 匹配：在 $X$ 中选择 $M$ 个连续字符，并用 $T$ 替换它们。

分析

问题一：我们什么时候能够替换？

按照样例来解释：

7 3
ABCBABC
ABC

可以看出，样例是放了三个 $T$ 。

在考虑 $S$ 的其他情况。如果 $S$ 为 ABBC 那么就是不可以的，因为无法用两个 $T$ 来组成，因为两个字符串都会失去前缀和后缀。

在自己列举几种后发现：

两个 $T$ ，前者没有部分后缀或者后者没有部分前缀是可以相匹配的，但是呢，两个并存是不可以的。

问题二：怎么做呢？

我们可以使用 DP 的方式记录状态 $d p_{i, j}$ 代表到第 $i$ 个字符，此时位置是 $T$ 中的下标几，然后表示能不能到达。

于是我们可以得到转移：当 $d p_{i - 1, j - 1}$ 成立时， $d p_{i, j}$ 和 $d p_{i, 1}$ 都成立，如果 $d p_{i - 1, m}$ 成立，那么对于所有的 $j$ ，都有 $d p_{i, j}$ 成立。

然后再判断一下两个字符串是否相等，如果不相等，把他换回不成立。

AC code：

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define fir first
#define se second
#define endl '\n'
#define debug puts("AK IOI")
using namespace std;
const int N = 2e5+5;
int n,m;
string s,t;
bool dp[N][10];

int main(){
	cin >> n >> m;
	cin >> s >> t;
	s=' '+s;
	t=' '+t;
	if(s[1] == t[1])dp[1][1]=1;
	
	for(int i = 1;i <= n;i++){
		for(int j = 2;j <= m;j++)
			if(dp[i-1][j-1]) dp[i][j]=dp[i][1]=1;
		if(dp[i-1][m]) for(int j = 1;j <= m;j++)dp[i][j]=1;
		
		bool ac=0;
		for(int k = 1;k <= m;k++){
			if(t[k]==s[i] && dp[i][k]) ac=1;
			else if(dp[i][k]) dp[i][k] = 0;
		}if(ac==0){
			cout<<"No";	
			return 0;
		}
	}if(dp[n][m])cout<<"Yes";
	else cout<<"No";
	return 0;
}

P9915 「RiOI-03」3-2 题解

更好的阅读

这是一道找规律的题目。

因为我个人习惯，以下部分使用从 $1$ 开始的下标讲述。

首先我们以 $1$ 来说：发现在第 $x$ 行 $y$ 列的连通块是可以直接连到第 $1$ 列的，所以很容易可以得出 $1$ 到 $y$ 列的连通块数量是 $2^{y} - 1$ 。

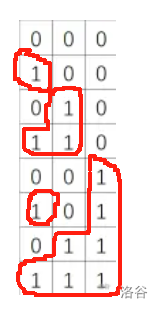
接着，我们考虑再后面的情况：

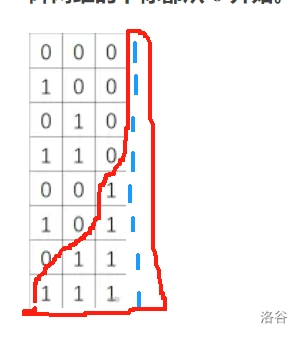
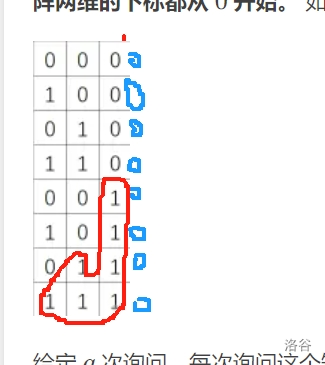
显然，通过观察会分为后面两种情况。一种是遇到了不一样的数字，那么久无法继续判断下去。如果是一样的话那么必定是增加 $2^{y - 1}$ 个连通块，于是，我们就可以用一个循环，一直增加 $y$ ，不断更新着连通块的数量。

如果考虑 $0$ 的情况也是同理。这里不过多解释。

但是我们还是会发现：这样的时间复杂度肯定过不去。

但是出题人给了善良的条件： $n \leq 10^{18}$ 。那么 $\log (n)$ 最多也就 $64$ 了，所以，我们在 $y$ 大于 $64$ 的时候特判掉即可。

于是优化到了 $O (q \log n)$ 。

上代码：link。

其中感谢 @tiger2008 在求助贴中告知需要特判。感谢好心人！

给个关注或一个赞呗！

[ABC333E] Takahashi Quest 题解

博客园

这算是又一次水 E 题。

本题题面要求最大值最小，第一眼是二分。但仔细想想，二分可能比较难写。于是我们考虑贪心。

一个药水能对应打败一个怪兽，然而想要药水在身上的数量最多时最少，换句话说：能晚拿药水就晚拿药水。

然而 $x_{i}$ 的范围是 $2 \times 10^{5}$ 所以不妨开一个栈来存储。每次遇到药水，直接堆进对应种类的栈中。

在遇到每一个怪兽的时候，再调用栈，栈顶的元素肯定是最近加入的，也就是离这个怪兽最近的药水。如果栈空，那么不合法，输出 -1。

因为我们最后输出的是第几瓶药水有没有捡，不是第 $i$ 时间有没有捡。所以在存栈的时候要在加一个一个数，也就是当时是第几个药水。怪物的时候取完了药水就在答案的数组中增加一下元素。

这道就做完了

赛时：link

int n;
const int inf = 0x3f3f3f3f;
const int N = 2e5+5;
int t[N],x[N];
stack<pair<int,int> > vis[N];//i类型的药水最后是什么时候出现
int q[N];
int ans2[N];
int cnt=0;
void solve(){
	
	cin >> n;
	for(int i = 1;i <= n;i++){
		cin >> t[i]>>x[i];
		if(t[i]==2){
			if(vis[x[i]].size() == 0){
				cout<<-1;
				return ;
			}
			q[vis[x[i]].top().first] ++;
			q[i+1]--;
			ans2[vis[x[i]].top().second] = 1;
			vis[x[i]].pop();
		}else if(t[i]==1){
			vis[x[i]].push({i,++cnt});
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++){
		q[i]+=q[i-1];
		ans=max(ans,q[i]);
	}cout<<ans<<endl;
	for(int i=1;i<=cnt;i++) cout<<ans2[i]<<" ";
}

signed main(){
//	freopen("std.in","r",stdin);
//	freopen("std.out","w",stdout);
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int TTT=1;
//	cin >> TTT;
	while(TTT--){
		solve();
	}
	return 0;
}

~~点个赞呗~~。

[ABC265E] Warp

首先，这一题很显然是一个 Dp。

考虑如何转移状态，因为一开始的坐标是 $(0, 0)$ 。

发现最后的坐标是 $(A \times i + C \times j + E \times k, B \times i + D \times j + F \times k)$ 。如果是统计最后的种类的话，那么就比较简单，枚举 $i$ ， $j$ 和 $k$ 。但是题目要求的是方案数，所以我们可以用一个三维 Dp，转移一下 $i$ ， $j$ 和 $k$ 时的方案数，很容易想，可以从 $i - 1$ ， $j - 1$ 和 $k - 1$ 分别转移。所以后面枚举 $i$ ， $j$ 和 $k$ 只需要累加其 Dp 状态即可。

不可行的方案用 map 存储特判掉即可。

上代码：

link

P10024「HCOI-R1」报名人数题解（未交审）

博客园。

我们会发现， $2$ 和 $3$ 的火柴个数是一样的， $9$ 和 $0$ 的火柴个数是一样的。

所以只有在 $12$ 到 $13$ 这样是合法的，自己推一下可以知道，最多只有连续两个。

而在 $l$ 到 $r$ 的长度大于 $9$ 的时候可以直接输出 $2$ 。

剩下的情况直接暴力枚举即可。

#define int unsigned long long
const int mod = 1e9+7;
//const int mod = 998244353;
const int inf = 0x3f3f3f3f,N = 2e5+5,M = 2e5+5;
const ll linf = 0x3f3f3f3f3f3f3f3f;
int l,r;
int tmp[15]={6,2,5,5,4,5,6,3,7,6};
void solve(){
	cin >> l >> r;
	if(r-l > 9) cout << 2;
	else {
		for(int i = l+1;i <= r;i++){
			int x=i,y=i-1;
			int cnt1=0,cnt2=0;
			while(x){
				cnt1 += tmp[(x%10)];
				x/=10;
			}
			while(y){
				cnt2 += tmp[(y%10)];
				y/=10;
			}
			
			if(cnt1==cnt2){
				cout<<2;
				return ;
			}
		}cout<<1;
	}
}

posted @ 2024-01-07 09:41 gsczl71 阅读(48) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· AtCoder Beginner Contest 复盘合集

· 2023CSP复赛/NOIP备战模拟赛复盘集合

· 考试心得1

· 【学习笔记】状压 dp

· 杭州 Day 4 上午状压 dp

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 使用C#创建一个MCP客户端
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· 按钮权限的设计及实现

公告

昵称： gsczl71
园龄： 1年3个月
粉丝： 10
关注： 4

+加关注

2025年3月

日

一

二

三

四

五

六

gsczl71

2024年拿下七级勾

2023年题解总和

洛谷P3161 [CQOI2012] 模拟工厂题解

洛谷 P6239 [JXOI2012] 奇怪的道路 题解

洛谷 P4872 OIer们的东方梦 题解

前言

题目意思

注意事项

本人犯的最大错误

AT_abc324_e [ABC324E] Joint Two Strings 题解

题目大意

思路

[ABC327D] Good Tuple Problem 题解

分析：

[ABC328D] Take ABC 题解

题目大意：

思路分析：

[ABC328C] Consecutive 题解

[ABC329D] Election Quick Report 题解

题目翻译

分析

[ABC329C] Count xxx 题解

插曲

问题翻译

分析

AT_abc329_e [ABC329E] Stamp 题解

题目翻译

分析

P9915 「RiOI-03」3-2 题解

[ABC333E] Takahashi Quest 题解

[ABC265E] Warp

P10024「HCOI-R1」报名人数 题解（未交审）

公告

搜索

常用链接

合集 (4)

随笔分类 (34)

随笔档案 (38)

相册 (63)

网站

阅读排行榜

评论排行榜

推荐排行榜

最新评论

洛谷 P6239 [JXOI2012] 奇怪的道路题解

洛谷 P4872 OIer们的东方梦题解

P10024「HCOI-R1」报名人数题解（未交审）