杂算法

高精度模板

copy老师的代码

@_xuefeng

#include<bits/stdc++.h>
using namespace std;
char ch[500000];
struct node{
    int s[1000000],len;
    void init(){
        scanf("%s",ch+1);
        len=strlen(ch+1);
        for(int i=1;i<=len;++i) s[len-i+1]=ch[i]-48;
    }
    void multi(){
        ++len;
        for(int i=len;i;--i) s[i]=s[i-1];
    }
    void divid(){
        for(int i=1;i<=len;++i) s[i]=s[i+1];
        --len;
    }
    friend bool operator <= (const node &a,const node &b){
        if(a.len^b.len) return a.len<b.len;
        for(int i=a.len;i;--i) if(a.s[i]^b.s[i]) return a.s[i]<b.s[i];
        return 1;
    }
    friend void operator -= (node &a,const node &b){
        for(int i=1;i<=b.len;++i) a.s[i]-=b.s[i];
        for(int i=1;i<=a.len;++i) if(a.s[i]<0) a.s[i]+=10,a.s[i+1]--;
        while(a.len!=1&&a.s[a.len]==0) a.len--;
    }
    friend void operator += (node &a,const node &b){
        a.len=max(a.len,b.len)+1;
        for(int i=1;i<=a.len;++i) a.s[i]+=b.s[i];
        for(int i=1;i<=a.len;++i) if(a.s[i]>9) a.s[i]-=10,a.s[i+1]++;
        while(a.len!=1&&a.s[a.len]==0) a.len--;
    }
    friend void operator *= (node &a,const node &b){
        node c;c.len=a.len*b.len+10;
        for(int i=1;i<=a.len;++i)
            for(int j=1;j<=b.len;++j)
                c.s[i+j-1]+=a.s[i]*b.s[j];
        for(int i=1;i<=c.len;++i) if(c.s[i]>9) c.s[i+1]+=c.s[i]/10,c.s[i]%=10;
        while(c.len!=1&&c.s[c.len]==0) c.len--;
        a=c;
    }
    friend void operator %= (node &a,const node &d){
        node b=d;int x=b.len;
        while(b<=a) b.multi();b.divid();
        node c;c.s[c.len=0]=0;
        while(b.len>=x){
            ++c.len;
            while(b<=a) a-=b,++c.s[c.len];
            b.divid();
        }
        c.len=max(c.len,1);//防止a<d的情况出不来数
    }
    friend void operator /= (node &a,const node &d){
        node b=d;int x=b.len;
        while(b<=a) b.multi();b.divid();
        node c;c.s[c.len=0]=0;
        while(b.len>=x){
            ++c.len;
            while(b<=a) a-=b,++c.s[c.len];
            b.divid();
        }
        c.len=max(c.len,1);//防止a<d的情况出不来数
        a=c;
    }
}n,m;
int main(){
    n.init(),m.init();
    n/=m;
    for(int i=1;i<=n.len;++i)printf("%d",n.s[i]);

}

KMP

update on 2023.11.17 NOIP前来复习板子，发现KMP整理的不是很到位，所以更新详细一些。

模板题

---

抽象的blog

浅显易懂的讲解视频：（dalao讲得太好了\(%%%\)）

备用网址

---

\(kmp\)（字符串匹配）的概念：

• 主串：被匹配的字符串
• 模式串：匹配的串
• 最长前后缀：一个字符串某个前缀后后缀相同，而且长度尽可能长

先讲暴力算法：
遍历主串，如果有一个字符与模式串不一样，适配了，那么主串就回到原来的位置+1，相当于一个 \(O(n \times m)\) 的复杂度.

因为复杂度过大，所以三位大佬(K,M,P）发明出了KMP算法，他的核心思想就是利用已知的数据，利用好，不往回头走，从而做到 \(O(n+m)\) 的复杂度。

设：

• 主串的下标是 \(i\)
• 模式串的下标是 \(j\)

他的做法就是不让i往回走，所以就能达到线性的时间复杂度

首先我们要预处理出 \(next\) 数组。

预处理完后。我们需要遍历一遍主串，按照暴力的思想一个个字符串相匹配，如果失配了。

那么我们设 \(k\) 为： 上一个下标（最后一个正确匹配的下标）的 \(next\) 数组。

然后将 $ j $ 加上 \(k\) ,也就是将模式串的下标往右移动k个下标，这样就可以跳过一些字符，但依然不影响答案。如果有一部分重复的例如: \(ABABC\) 中找 \(ABC\),自然，匹配到 \(C\) 的时候，就失配了。所以就找到第二个字符的 \(next\) 数组的值，为 \(2\)，所以直接跳过了前面的 \(AB\)，就直接配对了 \(ABC\)。

但是为什么这个 \(next\) 数组可以知道？

因为 \(next\) 数组存储的是主串中从头到这个下标的最长前后缀。如果他们有相同的前后缀，那么就可以跳过这些（注意：最长前后缀的长度不能等于计算的字符串，不然跳过整个字符串还有什么意义？）

当然，计算每一个字符串的最长前后缀也不是暴力的，我们可以分两种情况，如果遍历到 \(i\) ,那么已知\([1,i-1]\)的最长前后缀，假设其长度为\(k\),那么这个字符串的 \([1,k]\) 和 \([i-k,i-1]\) 相等，如果 \(i\) 和 \(k+1\) 能相等，那么 \([1,i]\) 的最长前后缀长度就是 \(k+1\) 否则，我们就按照之前的字符串的前缀。（具体看视频

更新部分：

数学课上拿着NOI辞典上写的一些笔记。。

For example：

第一种情况：

每一次比较 \(S_{next_{i-1} + 1}\) 的位置和 \(S_i\) 对比，如果匹配成功，那么显然是 \(next_i = next_{i-1} + 1\)。

第二种情况：匹配失败

假设首先知道 \(next_{12} = 5\)

ACBACDDACBAC 后面加入一个 B。显然 D 不等于 B。所以此时我们就要往前跳。

我们发现：ACBACDDACBAC 中前面的 ACBAC 的后面的 AC 和后面的 ACBAC 的后面的 AC。说的可能有点绕，不太好讲，具体还是看图吧。两个字符串相等，他们的后缀也一定相等。（说了跟说了似的

然而，前面的 ACBAC 的 \(next\) 数组是 \(2\)。因此其中的两个 AC 也是一样的。

ACBACDDACBAC 的前缀 AC 和后缀 AC 是一样的，于是下标往右移，发现左边的 AC + B 是与新加入的 B 相匹配。

于是就可以知道 ACBACDDACBACB 的 \(next\) 数组是 \(2+1=3\)。

因此，讲完了，感觉还是图画的清楚点。

实现流程：根据书中的话来说：

（1）设 \(j\) 为 \(next_{i-1}\) ，\(S_{j+1} = s_i\) 那么 \(next_i = j+1\)

（2）若不相等，\(j\) 需要变得更小，以满足 \(S_{[1,j]} = S_{[i-j,j-1]}\) 的最大值。即 \(j = next_j\) （其实上文主要解释了 \(j\) 为什么会等于 \(next_j\)。若此时 \(S_{j+1} = S_i\) 那么 \(next_i = j+1\)

（3）若仍然不相等，重复（2）直到 \(j=0\) 为止。

---

AC Code：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6+5;
char s1[N],s2[N];
int l1,l2;
int nxt[N];
int main(){
	scanf("%s",s1+1);l1 = strlen(s1+1);
	scanf("%s",s2+1);l2 = strlen(s2+1);
	for(int i = 2,j = 0;i <= l2;++i){
		while(j&&s2[i] != s2[j+1])j=nxt[j];
		if(s2[i]==s2[j+1]) ++j;
		nxt[i]=j;
	}
	for(int i = 1,j = 0;i <= l1;++i){
		while(j && s1[i] != s2[j+1])j=nxt[j];
		if(s1[i]==s2[j+1]) ++j;
		if(j==l2) printf("%d\n",i-l2+1),j=nxt[j]; 
	}
	for(int i = 1;i <= l2;i++) printf("%d ",nxt[i]);
	return 0;
}

有什么错误欢迎指出。

三分

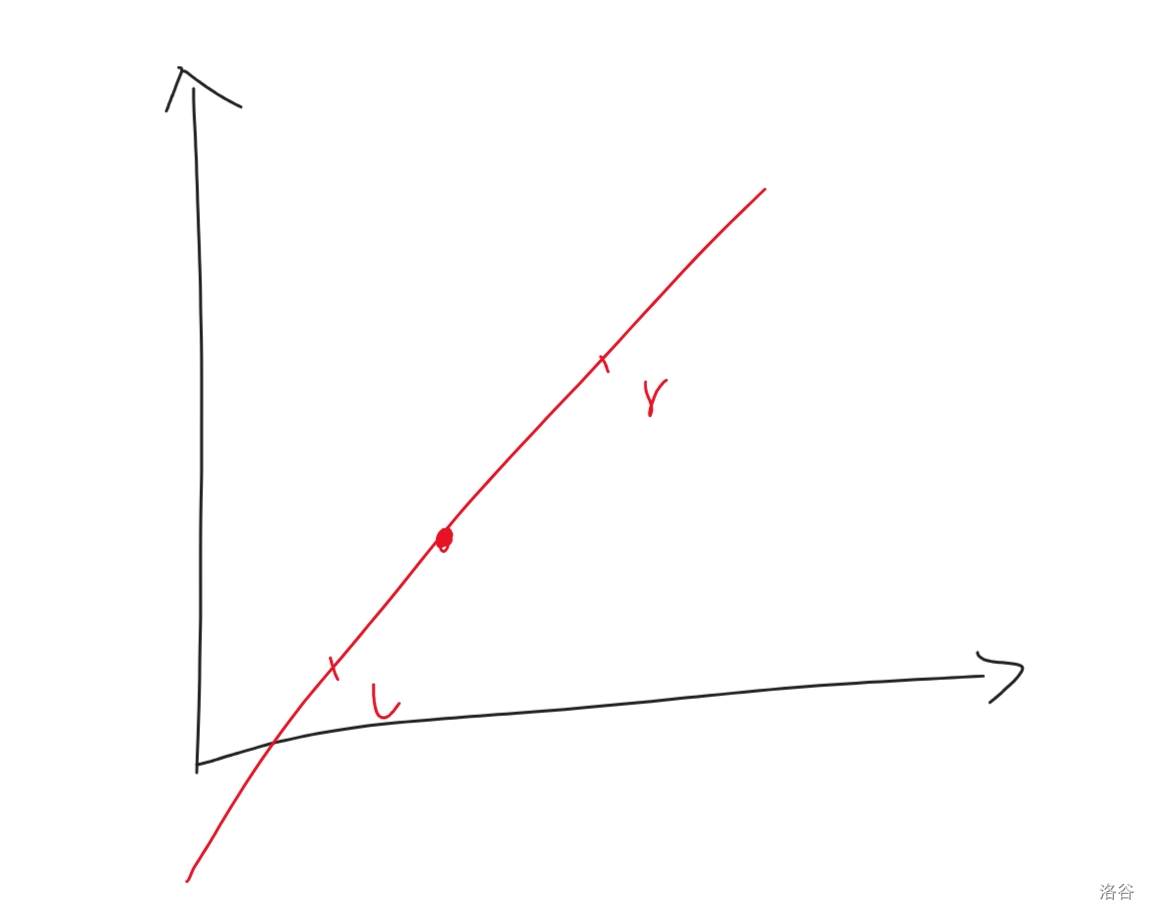
二分，那就是在一个有序的数组上查找某一个东西。抽象的说，那就是一个一次函数上查找一个点。（就是二分）
那么，三分呢？

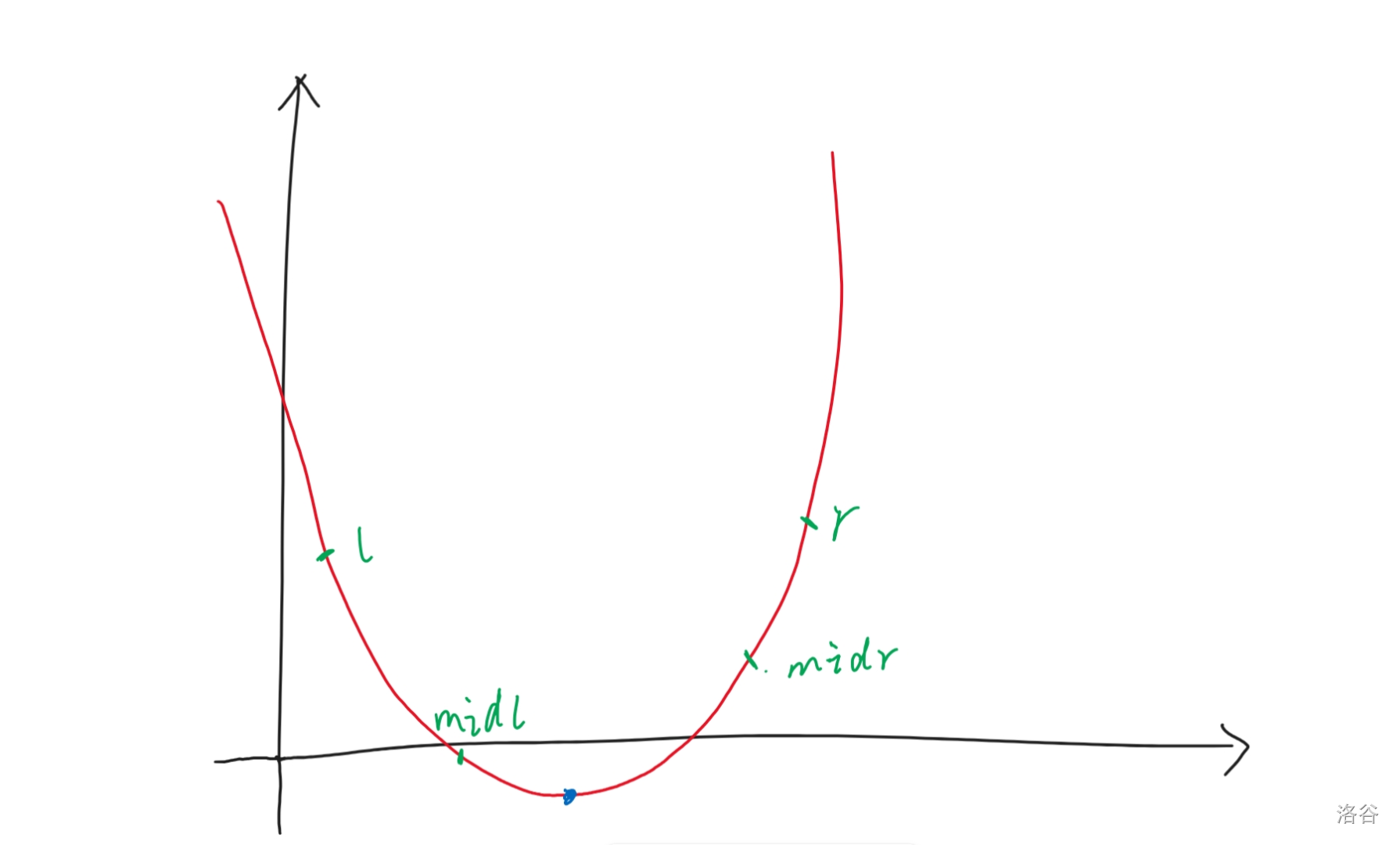
首先画一个抛物线。也就是一个二次函数。
三分干啥呢？就是找到蓝点的这个位置。
对比一下二分和三分。二分就是分成两份，中间是 \(mid\)，三分就是分成三份，有两个 \(mid\)，一个 \(midl\) 和一个 \(midr\)，都是平均三分来拼凑的。
如图，如果 \(f(midl) \le f(midr)\) 那么 \(r=midr\)，这是必然的。可以证明。
反之， \(f(midl) > f(midr)\) 那么 \(l=midl\)。

如果此时抛物线是开口朝下的，那么就是以上条件的相反。

但是我们要知道一个抛物线的开口是朝上还是朝下，就得用到求导公式，在这里就不细说。（是我不废

const int N = 20;
int n;
double a[N],l,r,mid,rmid,lmid;
double check(double x){
	//秦九昭公式
	double res=0;
	for(int i=1;i <= n+1;i++) res=res*x+a[i];
	return res;
}
void solve(){
	cin>>n>>l>>r;
	for(int i = 1;i <= n+1;i++) cin >> a[i];
	while(r-l >= 1e-8){
		double lmid = l+(r-l)/3.0,rmid = r-(r-l)/3.0;
		if(check(lmid) > check(rmid)) r = rmid;
		else l=lmid;
	}printf("%.5lf",l);
}
```