AtCoder Beginner Contest 复盘合集
AtCoder Beginner Contest 复盘合集
*2023.12.6 ABC312 VP(OI赛制)
这次的ABC相对比较难:红橙黄黄蓝绿绿,Ex(蓝)
A
B
稍微麻烦一点。
C
很水,直接Sort一遍即可。
D
稍微思考,可以得出一个DP,准确来说不太像DP
【警钟长鸣】我非常的弱智,\(n <= 3000\) 赛时写成1000。因为OI赛制,所以很弱智的挂分。
赛时因为无脑写压维被卡,换成二维即可过掉。
【坑点】闲着没事开滚动数组。
E
其实我一开始也是认为要维护每一个面,也就是每一个坐标,然后进行前缀和或者差分,但是觉得很复杂。后面突然间想到,其实暴力即可。为什么?因为如果你 \(n\) 个输入都直接遍历他的每一个 \(x,y,z\) 都是没有问题的。理论上会达到 \(n * 100^3\) 肯定会TLE。但是题目中有一个条件 每一个长方体的体积没有相交。意味着我们最多只会遍历 \(100^3\) 。非常nice。然后存到一个三维的数组当中后:
我们可以通过六个面来看周围是不是其他长方体,但是我们发现如果你往 \((x+1,y,z)\) 和 \((x-1,y,z)\) 是等价的。这是啥意思呢?因为你的 \(x-1\) 可以由 \(x-1\) 来判断它的 \(x+1\)(也就是 \(x\))来解决。
于是呢我们就可以通过三个if来判断。我真聪明。
然后再用一个set维护即可。
时间充裕:$O(100^3\times \log n) $ 非常轻松水了一道蓝。。
准确来说这应该是绿吧。
F
赛后发现巨水。可以说是思考10s,码量2min,调1.5h
甚至还请了何竺凌来帮我调。。。
最后发现的问题是在:
for(int i =1;i <= m;i++){
f[i] = max(f[i],f[i-1]);
}
整体思路是算t=0的部分的答案,和t=1,t=2的答案,然后最后组合在一起即可。
但是会发现如果需要选6个,但是只有2个可以选,那么会出现中间是空的,无法组合 ,这样,我们只需要把f数组渲染一遍即可。
总结:
这次其实F挺水的。大概是正常的D。赛时没切F主要是时间不够,而且一直认F是很难的。所以没搞F。然后D耽误了一点时间,总体来说发挥不太好。(OI赛制嘛,一般来说正常AT我都是罚时吃饱。。
*2023.12.9 ABC301 VP(OI赛制)
A:
签到,从头开始遍历,记录A和T的数量,如果相等,判断一下最后一个是什么如果是A则输出T,如果是T则输出A
B
签到,模拟即可
link
C
签到,依次遍历,如果存在不是 atcoder 这几个字符之外的有不同数量,那么就是不合法。
如果这些字符数量超过两个字符串的 @ 之和,那么也是不合法的。简单实现:
D
非常签到,很容易想到贪心,能取得就取,从前往后依次遍历。
先记录一遍如果所有 @ 都为 0 的情况下是多少,也就是最小二可能,然后
注意了:他这个地方是按照正序输入二进制的,所以应该是从前往后遍历才能取到尽可能大的值。
PS:【警钟长鸣】赛时挂掉的原因是位运算左移没有将1改成1ll,导致等于没有开long long。挂分/
E
是一道思维量少,码量大的题目。
由于猴子的数量很小,是18以内,所以我们只需要预处理逐个猴子之间的距离。大概是我们团队SFLS校园的一个弱化版。甚至只用BFS不用Dij,后面直接转移一下就可以了(类似Dp)但是因为下标(状压位运算的遍历范围)有些问题,调了很久,感谢@2020luke同学帮忙调过!!
一些位运算(状压)的细节,例如遍历到多少这些一定不能算少也不能算多。因为算少肯定影响结果,算多可能会导致重复计算或者是一些奇奇怪怪的东西出现,就是去了一些比n大的猴子。。。(当时没有考虑仔细,没有想到如果算多了会怎么样,比较马虎的大概设置了边界。zsy帮忙调了边界后过掉了。
稍微有点屎山。
总结:
这次是切了ABC,OI赛制比较难受,所以有些细节没有搞定,然而码量大的有没有码出来,码量小的又弱智丢分。所以下次还是要更加细心,不要因小失大。
2023.12.10 ABC321 VP(IOI赛制)
A
逐个拆位,然后与上一个比较即可
B
维护一下sum,最大值,最小值,枚举k进行答案的计算,做完了
C
发现\(n\)很小,可以打表。\(O(1)\)
写完发现题解区全是打表
D
先排序。然后做一遍前缀和。
枚举A,然后二分B,找到前面使用s,后面使用P的地方,然后进行\(O(1)\)计算。
F
拿一个球,拿走一个球,发现时间复杂度允许 \(O(qk)\)。于是,我们可以使用 DP 来记录和为 \(i\) 时的数量。
如果是新增,那么每一个 \(DP_i += DP_{i-x}\)。注意要倒序,因为前面的做完不能影响到后面。
如果是减少,那么每一个 \(DP_i -= DP_{i-x}\)。但是这个地方是需要正序进行,因为一个球是由 \(i-x\) 来的,所以应当减去他没有这个球的时候的数量。然后后面的却要调用前面的来,也就是说,\(DP_i\),一定是从 $DP_{i-x} 转移来才能为 \(DP_{i+x}\) 的转移带来可以减少的数。
核心代码就是分别讨论,套一个for循环,然后进行上述的逐一转移。
注意的细节:取模的时候减法要 + mod % mod
加法就是正常的 % mod
Ps:取模的地方要注意了。
2023.12.12 ABC320 VP(IOI赛制)
A
【警钟长鸣】别用pow!!不知道为什么,用pow会精度损失,所以直接手写
link
B
直接 \(O(n^3)\) 暴力枚举即可。
link
C
一开始有一些理解错误。
其实他的意思就是每一个字符串的 t 是不同时间,所以不妨讲每一个字符串直接复制三倍,然后暴力枚举。\(O(27 \times M^3)\)
link
D
我们可以利用已经知道的(1,1)的坐标,然后bfs广度延申,将所有的点都搜出来。时间复杂度足够 \(O(m)\)
【坑点】要建立双向边,因为如果可以从 a 推向 b,也可以从 b 推向 a,然而,x和y要做一下取反。于是就搞定了。
link
E
可以针对 n 个人进行处理。用一个set维护,然后每一次找到最小值,不断往后二分下一个点,如果存在的话,那么ans加上那个,否则直接break
一开始用数组手写二分。可能细节的问题,卡了很久,最后重构就AC了。时间复杂度是 \(O(m \log n)\)
link
*2023 12.12 ABC279 VP(OI赛制)
A
老师都说很弱智,所以很弱智。
link
B
查找子串?对,Kmp,板子。。 但是实际上 \(n=100\) 直接暴力枚举两个字符串的左端点,遍历一遍,结束。
link
C
很显然,直接存储每一列,sort一遍即可。
link
以上就是我赛时切的 很弱智。。。没错,两个小时干了三个红题。
D
这是一道黄。但我赛时没有切。很显然,取最小值,因为g在一个地方是乘,另一个地方是除。显然是一个抛物线。那么?三分!!正好前几天学了三分。
然而我两个小时都在调这一题。。。
总结出来,有一玄学的点:
改完之后不仅能使你的样例过不了,还可以使你成功AC!!
【侯森凯学长之邪教】不会二分边界怎么办?很好办:
if(r <= l+5) printf("%.10lf",min({check(l),check(l+1),check(l+2),check(l+3),check(l+4),check(l+5)}));
愉快的解决掉了不会二分边界的问题。
Ps:因为翻译比较简练,所以不知道g是整数!!瞎搞了半个多小时。然而老师亲切的提醒了后,还是一直挂着。于是一只眼睛调D,一只眼睛看E题思路///最后是两个都没有完成啊啊。
link
E
@2020luke 因为赛时切了这题(绿)跟我炫耀了一个小时。/
是一个Dp表示状态。。
需要预处理:
- 每一个点到最后在什么位置(没有删除操作)。
然后我们可以进行 \(O(m)\) 的for循环。设 \(DP_i\) 表示的是到 \(i\) 个操作的时候 \(1\) 点的位置。
本题难点主要在于需要想到几个数组互相映射出来的。
F
其实想了想并不难的。
很巧妙地运用了并查集。
很正常的存一个并查集,我们把每一个球和箱子都设做一个并查集中的点。
然而,合并的时候直接合并嘛。哪有那么简单。想到合并之后有可能还会有其他点的加入,这样就会发生错误。
所以,我们在合并了两个箱子之后,原来被合并的那个箱子显然是不能再用的,于是我们可以新开一个箱子。然后用一个数组映射一下,记录他实际是什么箱子。
在很多个数组的映射中,再套上一个并查集,结束。注意一下细节。考虑到箱子可能很多个所以我们要开三倍的空间足够我们折腾。
膜拜一下学长,场切EF!!
*2023.12.14 ABC278 VP(OI赛制)
A
没有场切很弱智,没有考虑到 \(k > n\) 的情况。
luke因为ABCDE都没挂分,又在炫耀。。。
link
B
因为时间复杂度十分充裕,所以直接枚举答案,进行判断即可。场切
link
C
发现数据范围是\(1e9\)无法当下标来存,所以直接想到set维护时间复杂度 \(O(q \log n)\) 可以过掉。在过程中直接二分即可。实际上可以使用“高科技”find函数一键解决。/场切
link
D
其实做法启示于线段树中的“Lazy-tag”就是等到要查询的时候再来判断是否要更新,大大减少了清空的时间复杂度。在每一个数开一个结构体,存一下最后修改的时间,如果发现在这个时间后有操作进行了清空,于是再给他做清空。
场切
link
E
只需枚举一下每一个hw的矩阵的左上角的下标,然后类似滑动窗口的做法,逐个往右移动,然后只需要稍微修改维护一下边界的加减即可。因为 \(k\) 是 \(300\) 级,所以直接开个数组可以统计个数,所以能够实时维护ans答案/
场切
link
F
其实并不难,不知道为什么考场没有搞出来,没了一个小时。
实际上是一个状压Dp,想到了,但不知道具体怎么搞。我们可以设\(DP_{i,j}\) 代表\(i\) 这个状态下面以 \(j\) 这个字符出结尾的能否必胜。然而,\(n<=16\)级的数据完全可以状压瞎枚举。通过转换一下,这个必胜,那么如果到达他之后的一个点那就是必输。很显然的博弈论嘛
最后只要有一个必胜,那就是first胜利,毕竟他是主动权的嘛。如果一个没有,那么就是Second 胜利。
感觉一有点博弈论就不行了。 场切不过黄,太弱了,下次加油!!
link
2023.12.16 ABC333
A
主打个弱智
link
B
第一眼:那么水,第二眼:WA!,第三眼AC了。抽象没有注意到是环,【不看题】+1
link
C
全场中最难的,我想到了贪心,我想到了打表,我想到了DP,我想到了预处理,但是我没有想到暴力,原来是暴力就可以过了也。菜就菜,别狡辩
link
D
非常简单的一眼题目。只用维护 \(1\) 的子树大小之和,然后减去最大子树的的大小,结束。。
link
E
稍微一丢丢的思考量,边想边写=AC。因为尽量保持每时每刻的背包重量最小,所以不妨在打一个怪兽前拿一个里此时最近的药(假设你可以穿越时空往回走。那么我们可以用一个stack维护。在遍历 \(1-n\) 的时候,如果是 \(1\) 那么就在stack里面添加 \(x\),然后,到了操作 \(2\) 的时候在栈里弹出栈顶的(肯定是目前情况最近的)。注意:在维护栈的时候要使用pair,这样才能维护到你之前取的药是第几个。然后如果这个地方取了药,那么前缀和++,打怪兽这个地方--,于是跑一边前缀和,实时求最大值即可。
话说,这玩意最大值最小是不是可以二分?,但好像又不可以,所以说:最大值最小,最小值最大不一定是二分,有可能是贪心,暴力。
*2023.12.22 ABC265 VP(OI赛制)
A
注意细节,y 有可能更不划算。
B
OI 赛制 WA 了,题目描述不是特别清楚,t = 0 的时候也是合法的。
C
过了,随便一个while循环实时维护即可
D
读题假了,要求区间 \(x ~ y-1\) ,我搞成 \(x ~ 任意\) 。成功WA 掉 hack点,赛时数据竟然都能过!!!
link
E
首先,这一题很显然是一个 Dp。
考虑如何转移状态,因为一开始的坐标是 \((0,0)\)。
发现最后的坐标是 \((A\times i + C \times j + E \times k,B\times i + D \times j + F \times k)\)。如果是统计最后的种类的话,那么就比较简单,枚举 \(i\),\(j\) 和 \(k\)。但是题目要求的是方案数,所以我们可以用一个三维 Dp,转移一下 \(i\),\(j\) 和 \(k\) 时的方案数,很容易想,可以从 \(i-1\),\(j-1\) 和 \(k-1\) 分别转移。所以后面枚举 \(i\),\(j\) 和 \(k\) 只需要累加其 Dp 状态即可。
不可行的方案用 map 存储特判掉即可。
上代码:
赛时切了。
F
有点懵,目前未解决,过两天琢磨琢磨再补上。
现在懂了。。。
直接把我的题解copy上来咯。
考虑 Dp,可以先设 \(dp_{i,j,k}\) 为前 \(i\) 维,\(r\) 到 \(p\) 所累积的距离为 \(j\),\(r\) 到 \(q\) 累计的距离是 \(k\)。于是 \(dp_{i,j,k}\) 从 \(dp_{i-1,j-|r_i-p_i|,k-|r_i-q_i|}\) 转移来。
因为有绝对值,所以得要进行分类讨论。具体情况如下。
放上这张图片:
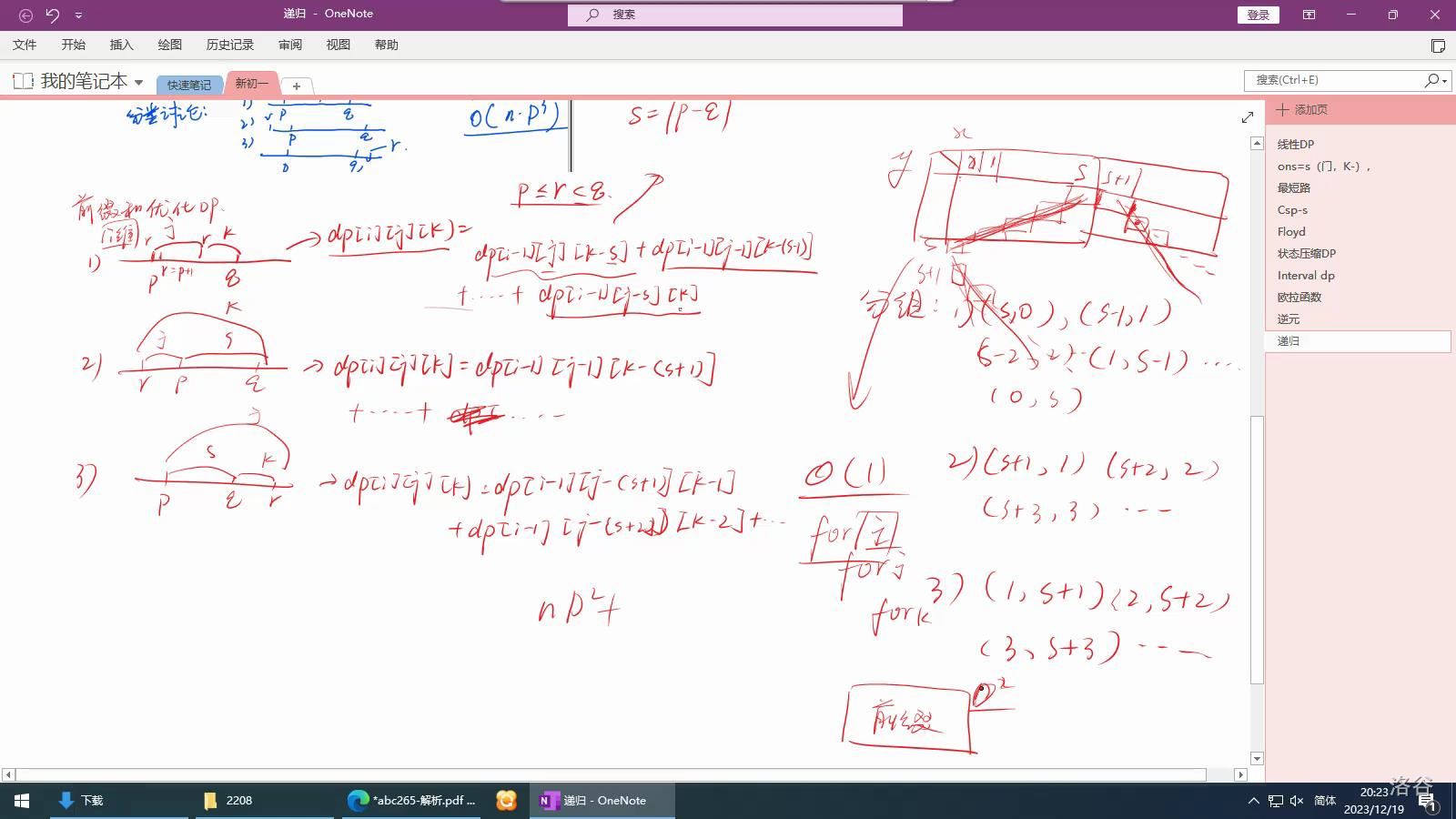
注:图片中的文字均有在下文提及。主要还是为了展现教练的灵魂画图。
设:\(x = |p_i - q_i|\)。
不妨先对正常的情况尽心分类讨论一下。
- 第一种情况:\(r_i\) 在 \(p_i\) 与 \(q_i\) 中间。\(dp_{i,j,k} = dp_{i-1,j,k-x} + \cdots + dp_{i-1,j-x,k}\)。
- 第二种情况:\(r\) 在 \(q_i\) 和 \(p_i\) 的左边。\(dp_{i,j,k} = dp_{i-1,j-1,k-x-1} + dp_{i-1,j-2,k-x-2} + \cdots\)。
- 第三种情况:\(r\) 在 \(q_i\) 和 \(p_i\) 的右边。\(dp_{i,j,k} = dp_{i-1,j-x-1,k-1} + dp_{i-1,j-x-2,k-2} + \cdots\)。
但这是一个 \(O(n D^3)\) 的暴力,无法通过。所以考虑如何优化这个 Dp,想到前缀和优化。
还是像刚才一样,分类讨论前缀和,因为情况的不一样,我们会发现第二第三种情况其实比较类似的,所以我们可以分成两个前缀和来写。
-
第一种前缀和:包含着上述暴力中的第一种情况。由于我们发现 \(j+k\) 一直是一个数,显然这是一个反着的对角线,可以抽象的理解就是从右上角连向左下角,说白了,就是主对角线的垂直对角线。\(qzh_{j,k}\) 来表示 \(dp_{i-1,0,k+j} + \cdots + dp_{i-1,j,k}\) 这条对角线,记录他的累加和,到最后状态转移计算中直接调用就可以咯。
-
第二种前缀和:包含着上述暴力中的第二和第三种情况。由于 \(j-k\) 是不变的,所以是一条平行于主对角线的线,可以理解为第一种前缀和的垂直的线段。那么我们显然需要再开一个前缀和数组来记录,毕竟方向都是不一样的,怎么能够共用呢!于是,定义:\(qzh2{j,k}\) 从这一条线开始连到 \(dp_{i-1,j,k}\) 的值。第二种情况中:\(dp_{i-1,s,0}\) 开始,第三种情况中:\(dp_{i-1,0,s}\) 开始。
这只不过是更加严谨的说法罢了。
所以呢?
做完了,只需要在状态转移的时候压缩掉一个 \(O(D)\) 的时间复杂度。
我认为吧,其实前缀和的优化并不是特别难,说白了就相当于预处理一些东西而已,但是这种解法确实也是难想,只不过是教练带着才做出来。实际上这一题的难度还是有的!
link。
2023.12.24 ABC334
开题四分钟竟然拿到rk5/
A
比较弱智
link
B
最难了,我切了很久啊。换了很多种方法。
link。
核心代码:
int a,m,l,r;
cin >> a >> m >> l >> r;
l-=a,r-=a;
if(l>0) cout<<(r/m-l/m+(l%m==0));
else if(r>0) cout<<(r/m+(-l)/m+1);
else cout<<((-l)/m-(-r)/m+((-r)%m==0));
我们可以通过取模的性质。然后知道一个数模 \(m\) 等于 \(a\) 模 \(m\) 的地方有树。首先我们不妨先将 \(a\) 的位置看成 \(0\) 点。我们可以抽象的理解,利用 \(m\) 分了很多个区间,每一个区间都是长度为 \(m\),然后算出 \(l\) 和 \(r\) 分别属于什么区间,然后两个区间编号一减,其实就是他们中间树的个数。如果左端点在树上,还要再加一。
因为涉及到正负性的关系。所以需要稍微分类讨论一下,然后注意细节即可。
罚时3次。
C
首先,我们可以分两种情况讨论,如果是偶数,那么排完序之后 \(a_i - a_{i-1}\) 算出来即可。
奇数我们可以预处理一个前缀和和一个后缀和。然后枚举中间哪一个是不用取的,然后使用 \(O(n)\) 时间复杂度解决。
注意一下细节,首先你遍历的时候一定是 \(+2\) 这样跳的,如果是 \(+1\) 的跳就会错,我被卡了很久。
link。
D
最简单的一道。只需要前缀和一遍,二分即可。
link
*2023.12.27 ABC267 VP (OI赛制)
A
很简单的题目。
B
题目比较抽象,理解了一下,实际很简单,因为时间复杂度随随便便搞都没有问题
C
没有考虑负数,ans初始0喜提保龄
D
考场想复杂了,认为前面的转移需要用到树状数组维护最大值,实际上,写出来后样例1AC1WA,后面想到其实一个数组实时滚动即可。于是一个dp一个a互相转移就行了,但是最后还是保龄了。老师一讲就恍然大悟,这不是背包板子吗。行了,就过了。
E
顺手一丢题解放上来:
首先,出题人非常滴友善,提供了最大值最小字样,学过 OI 的选手一样就看出来了!二分!!
确实的,这一题就是二分。
我们可以直接二分答案,然后根据 \(mid\) 去进行广度优先搜索,遍历到的这个点的所有连接的点权之和必须小于这个 \(mid\),不然就是不可以加入,然后在广搜遍历的时候,如果这个点 \(i\) 合法,还要将这个点 \(i\) 所连向的所有点 \(j\) 减去一个 \(a_i\),使得实时更新每一个点目前周围的点的点权之和。
于是通过一个搜索板子题目,我们愉快的 AC 了。
link。
我也不知道我是为啥的没看出来,明明很典型啊。可能是没他仔细想吧,几乎整个考试过程都一直在被D弱智着。
F
题解通道关了!喷!
赛时的时候想到了树上距离,倍增,可以用LCA来解决。大概就是分情况倍增,我也不知道我是怎么想的,竟然只想到两种可能,就是跳祖先,和跳孙子,然后跳孙子竟然也写了倍增!我太聪明了。。
首先我们肯定尽可能让 \(u\) 有一个可以到达尽可能远的结点,例如他最远的结点是 \(p\) ,那么 \(p\) 开始往下建一棵树,然后在树上找 \(u\) 的 k 级祖先即可。很容易想到可以建立倍增表来搞,但是实际上,根据dfs序的定义,可以知道假设这个点是第 \(x\) 个遍历到的,那么它的k级祖先便是 \(x-k\) 遍历到的点。所以说,可以直接 \(O(1)\) 解决掉祖宗问题。
实际上直接跑三遍dfs
第一次从1开始遍历,找到最远的点,就是树的直径的一端,然后再找最远的点,就是树的直径的另一端。
所以我们在两个直径端点跑dfs的时候顺便就可以看一下这个点的是否被查询了。然后对ans进行记录,一般对于 q 组询问都是在线回答,但是这种离线的处理方式也是非常的巧妙。
G
题目描述
给定一个正整数序列 \(A=(a_1,a_2,\ldots,a_n)\),问有多少个 \(1\sim n\) 的排列 \(P=(p_1,p_2,\ldots,p_n)\) 满足:
- 存在恰好 \(k\) 个整数 \(i(1\leqslant i\leqslant n-1)\) 满足 \(a_{p_i}<a_{p_{i+1}}\)。
思路
有那么一点点抽象,但是还是可以理解的。
我们不妨将问题转化一下:将 \(a\) 数组重排变成 \(b\),然后 \(b\) 上有 \(k+1\) 个连续的不上升序列(递减)。
如图:

这一张图片中黑色点代表着每一个 \(a_i\) 的值,然后蓝色的线段代表着每一对 \(a_{p_i}<a_{p_{i+1}}\),红色的线段则是连续的不上升序列,然后第 \(i\) 个连续的不上升序列的开头和第 \(i-1\) 个连续的不上升序列的结尾可以形成一对(\(a_{p_i}<a_{p_{i+1}}\))。相当于要 \(k+1\) 个连续的不上升序列。
因为 \(a\) 的顺序不重要,不妨先排序。
我们可以理解,每一次加入的 \(a_i\) 有两种情况:
- 第一种 \(a_i\) 加在所有数之前。如图:
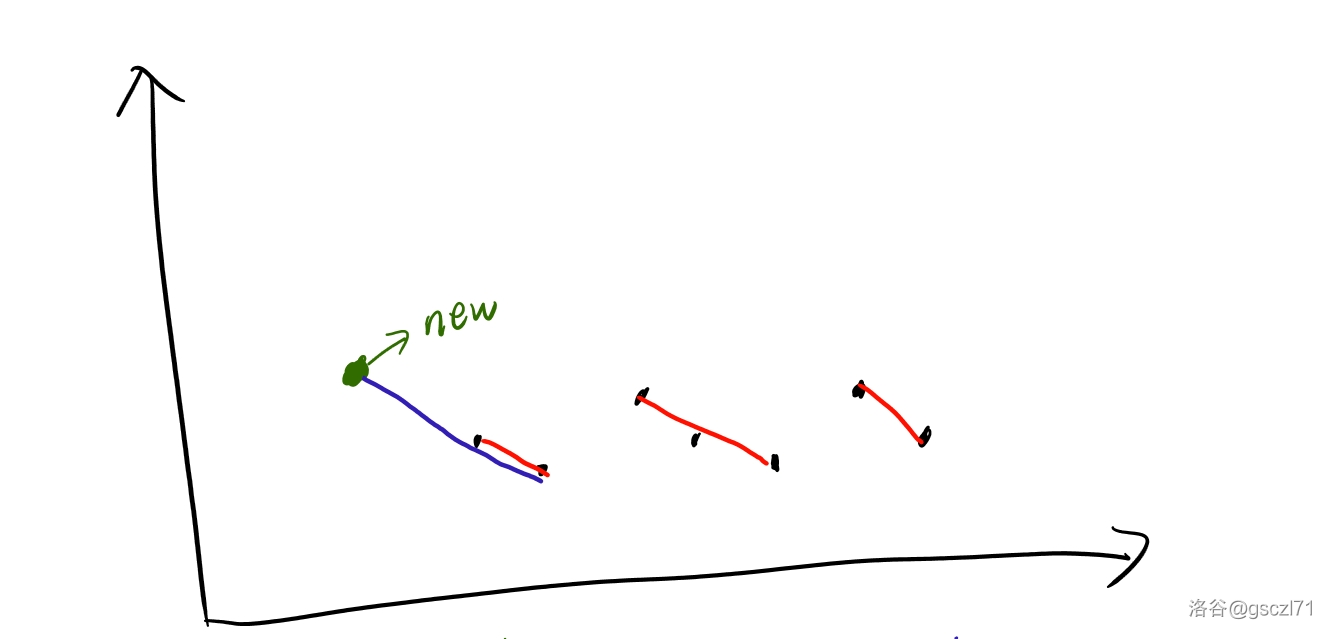
图中绿色点为新加入的点,由于这个点肯定是目前最大(大于等于其他点)。肯定能与目前的第一个点的红色线段连在一起(即蓝色线段),换句话说,就是这种情况连续的不上升序列是不变的。
- 第二种 \(a_i\) 加在中间。如图:

图中蓝色的点加入使得一个红色的线段变成了两个独立的线段,所以说连续的不上升序列加一。
但是,聪明的你会发现:如果有重复怎么办?
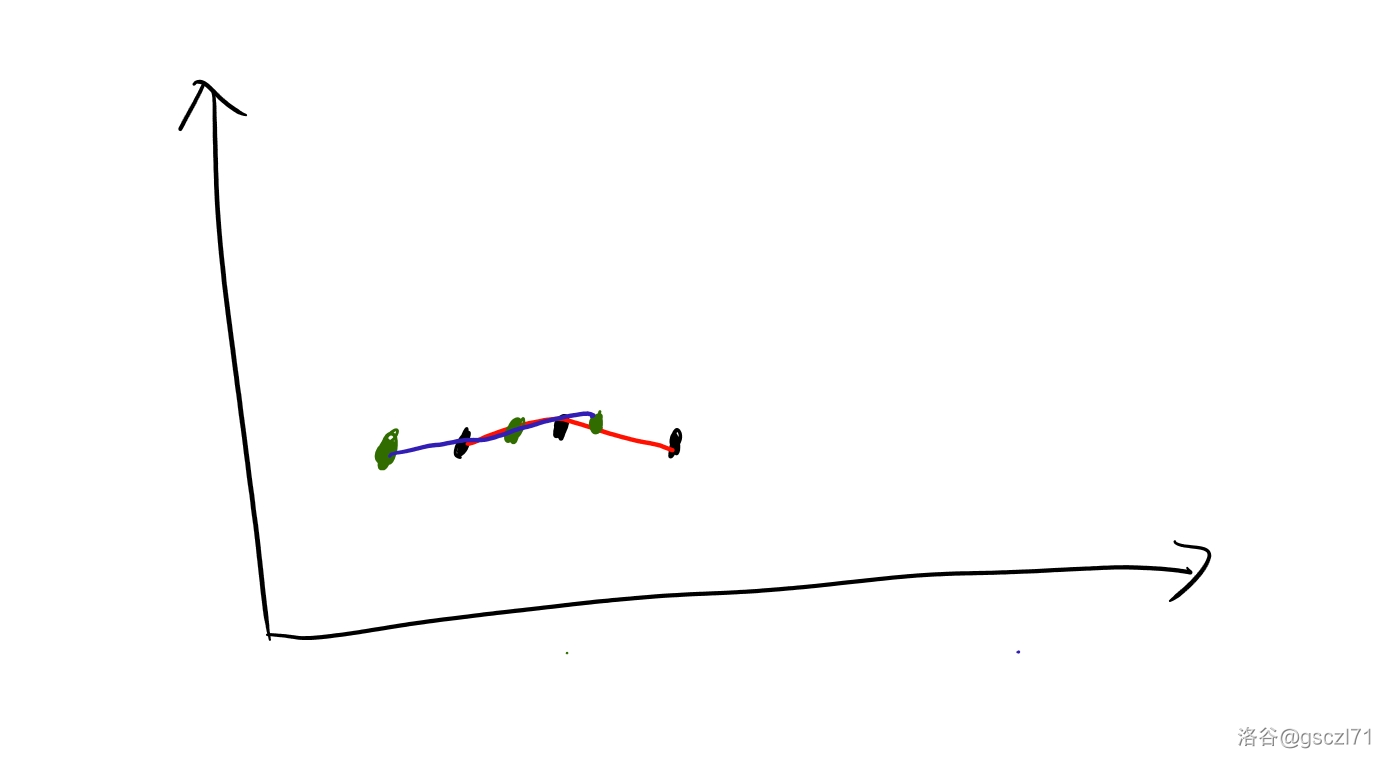
例如,这个是第一种情况,如果有相等的点那么我们可以有多种可能,图中的绿色点都是合法的方案。假设之前已经有 \(vis_x\) 个点等于 \(x\),那么此时必将是可以放在 \(vis_x+1\) 个位置上,\(1\) 是之前的连续不上升序列的个数。所以,我们只需要实时维护 \(vis\) 即可。
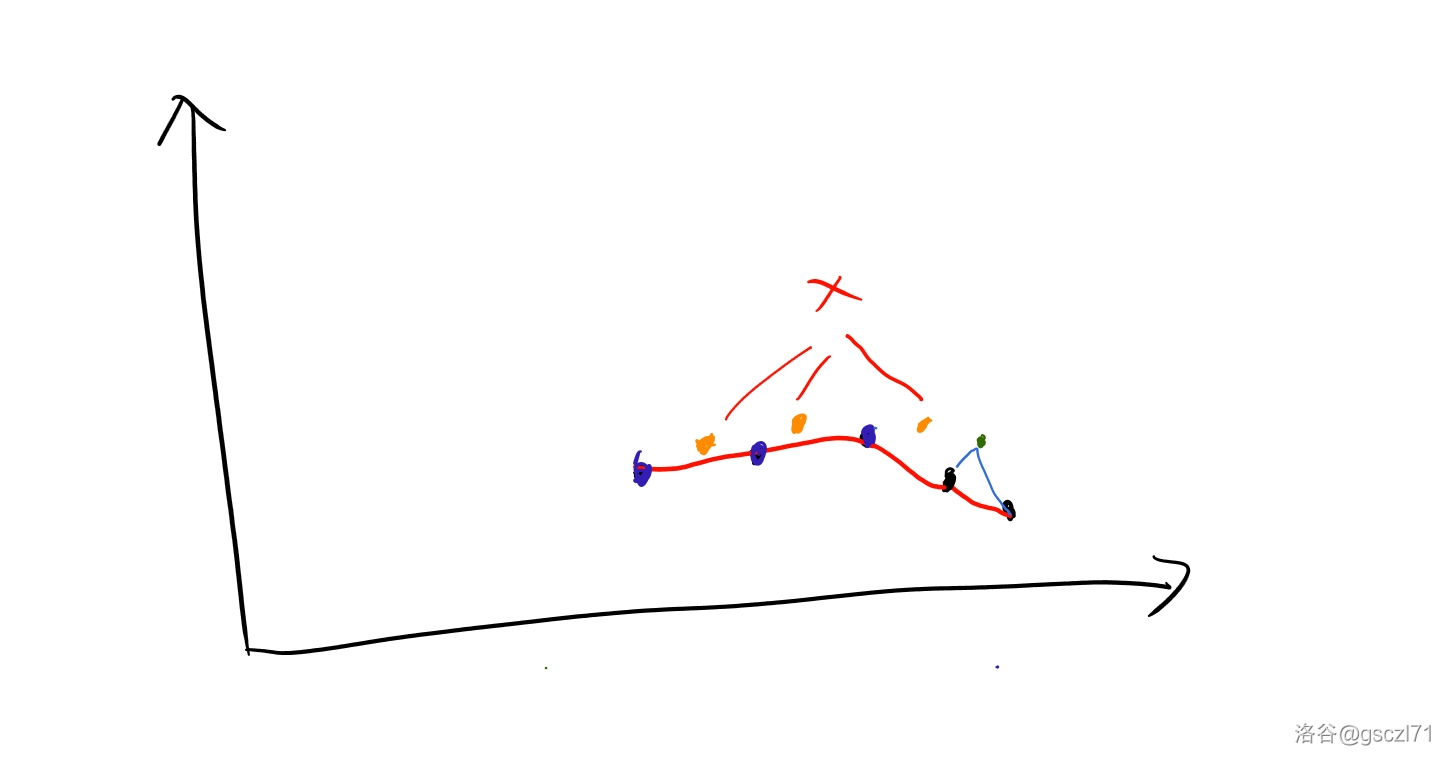
这是第二种情况。从图中可知这个点只能放在绿色位置,不能放在橙色位置,为啥呢,因为它等于了,所以没办法多造一个连续的不上升序列了。那么方案数就是 \(i-j+1-vis_x\),\(i-j+1\) 就是正常的空位的个数,然而 \(vis_x\) 个数挡住了,于是就减掉。
这样我们就可以得到状态转移方程了,使用 DP 进行状态转移,时间复杂度 \(O(nk)\)。通过咯。
link。
*2023.12.30 ABC270 VP(OI赛制)
A
场切link。
B
赛后还交了四发才过,恶心的if啊。八个if所组成的奇迹。link。脑残cout的写错了。
C
浅浅的写了个广搜,搜到了,就往前栈里找,然后找到答案.link。
D
实际上,令 \(dp_i\) 代表石头数量为 \(i\),先手可以拿到最多数量的石头。如果下一步拿走 \(a_j\) 剩下了 \(i-a_j\) 个,对方最多也只能拿 \(dp_{i-a_j}\)。于是,剩下 \(i-dp_{i-a_j}\) 可以拿走。
状态转移方程就是 \(dp_i = max(i-dp_i-a_j)\) 转移过来的。
link。
E
很容易想到,每一次拿很多圈,先排序,然后每一次可以拿掉 \(a_i - a_{i-1}\) 层。但是有很多细节要判定,例如你那完这一层还有一层不完整的,就直接遍历,幸好赛时过拍切下来。赛后hzl说可以二分,想想也是,不然怎么是黄呢,二分的话码量就很小了。
link。
F
我们可以建两个虚拟结点,相当于一个是海港,另一个是机场,这是图论常用的套路,我咋没想到呢。错,我都没看题。然后跑最小生成树板子就可以了,因为要不要海港,要不要机场,4种情况分类讨论即可。
link。
*2024.1.3 ABC271 VP(OI赛制)
A
秒link。
B
秒link。
C
想复杂了,不用排序不用去重,一个标记就可以了link。
D
写了个记忆化搜索,实际上就是DP,但是感觉DP转移比较复杂。赛后老师一说背包板子,瞬间明白。。(大雾link。
E
可以用 DP 来解决。\(dp_{i,j}\) 代表着第 \(i\) 条边,点 \(1\) 到 \(j\) 最短距离。考虑转移方式:如果需要这个边 \((u,v,w)\) 那么,\(dp_{i,j} = dp_{i-1,u} + w\)。不需要这个边:\(dp_{i,j}=dp{i-1,j}\)。\(j\) 其实就是 \(v_i\)。
空间的限制,所以我们没法开二维数组来存储。发现 \(i\) 从 \(i-1\) 转移来,所以说,我们可以压维。因此就得到了正解。
link。
F
赛时想到了 meet in middle。但是看到了 \(n <= 20\)。不是 \(2^{n^2}\) 的复杂度吗?我真聪明。没想到只有往下往右,所以应该是 \(2^{2\times n}\)。显然会炸。所以 meet in middle。\(2\times 2^n\) 时间复杂度。因此水了一道绿色。
然后双倍经验,蓝又AC一道。
link。
*2024.1.4 ABC268 VP(OI赛制)
A
秒link。
B
秒link。
C
一开始先看了E,发现这一题是简化版,没想到是从最大值->最小值,调了半天(乐,后面发现样例玩不懂乐!ok祭,半个多小时白白送葬。最后还是:秒link。
D
考场专注 C,E 都一眼没看。赛后后悔,发现巨水。
以下是题解:
这一道题的精髓在于:暴搜。
一看 \(n \le 8\)。简直就是随便搞都可以。他是任意一种情况都可以,那就更简单了。考虑最最暴力的写法。枚举每一个点开始,然后枚举多少个 _,然后深搜下去。肯定是会超时。
所以考虑剪枝,通过计算可以得出来之后会不会超过 \(16\) 的长度。如果会超过,则退出,这其实已经加快了很多,所以,一提交,你就发现水了一个绿题。
link。
E
赛时知道了大概的解法,很容易想到先递减再递增或先递增再递减。但是细节就是差那一点,没调出来,一个多小时相当于罚坐。。
赛后何竺凌搞出了简洁写法!!太酷啦。一看就懂,不愧是大佬!!
以下是题解:
首先,对于每一个人 \(i\) 都有自己想要匹配的 \(i\) 餐桌。于是想到,转动餐桌会使得餐盘离这个人出现两种情况:
- 先递减再递增
- 先递增再递减
很容易想到,这其实可以看作一个很多条一次函数的直角坐标系。我们需要手推一下每一个点的地方,然后跑两遍前缀和就可以解决。由于奇偶的情况不一样,所以要分讨,但其实我们只需要建立顶点 \(i+\dfrac{n}{2}+1\) 和 \(i+\dfrac{n+1}{2}+1\) 即可。
因为我们想要把直线直接延伸到比 \(n\) 大的地方以免发生取模错误。所以直接 \(+n\) 地套上去。
link。
F
这题使用贪心来解。首先我们用两个变量 a:代表这个字符串数字之和,b代表x的之和如果最后的排列 \(i<j\) 那么有 \(a_i.b * b_j.a\)。反之 \(i>j\) 那么有 \(a_i.a * b_j.b\) 为了使得答案最大化,只需要对其进行sort一遍,如下:
bool cmp(node a,node b){return a.a * b.b < a.b*b.a;}
核心代码,按照这样的构造方式去模拟就可以得到答案。
link。
2024.1.7 ABC335
C
像是一个贪吃蛇,然后每次向某个地方走动,然后后一个点会来到前一个点的位置。我们可以直接开一个 vector 来存储坐标的变化(做一个第 \(i\) 时刻的前缀和)实际上的作用,就是在第 \(i\) 时刻坐标是在哪。对于时间为 \(0\) 的时候,可以看作第一个点是 \(n-1\) 时间的位置,最后一个点是 \(0\) 时间的位置。然后每一次询问只需要查询数组中时间减去第几个点的下标,就是答案。
link。
D
实际上就是要你从中间走,然后每一个点都遍历到,输出它的编号,由于样例是一环一环的,所以我误解了题意,其实直接遍历,到了不可以的地方就回退就行了。
本代码的实现是先处理好每一圈的环数然后遍历每一个环,如果遍历不了,往左边走。
link。
F
博客园。
听说有原题,但好像不太像。
很显然 DP。
实际上挺玄学的做法,令 \(dp_i\) 代表第 \(i\) 个点结尾的方案数。直接暴力肯定会超时。所以玄学地开两个 DP 数组,如果这个倍数间隔大于 \(10^3\) 那么肯定暴力是没有问题的。所以这种情况直接暴力跳。否则,开另一个数组来存,\(dp2_{i,j}\) 代表倍数间隔为 \(i\),距离这个倍数取模的结果为 \(j\)。然后在每一次遍历的时候把之前的 \(dp_2\) 数组转到 \(dp\) 数组上。直接看代码,毕竟个人感觉两个 DP 数组之间转换有那么一点点玄学。
link。
2024.1.8 ABC273 VP(IOI赛制)
A
直接暴力
link。
B
调了很久,最后实在不行,看了看别人的复盘,好像差不多,样例没过的我想赌一波,结果还真过了,估计是pow的精度问题link。
C
这是一道语法题,就是在map和set中间乱搞搞出来的link。
D
以下是题解:
我们需要实时维护位置,然后考虑二分这里最近的那个障碍物是否对下标有影响,所以可以用 set,智慧的你发现了下标会到 \(10^9\) 所以,要套一个 map。
这道题其实考了你会不会 set。2020luke 在题解中表示:别用set,因为会超时。
但是我用了 set,没有超时,是怎么回事呢?
很简单,对比一下两行伪代码:
set.lower_bound(x);
和:
lower_bound(set.begin(),set.end(),x);
有什么区别呢?
科普一下,前者时间复杂度是 \(O(\log n)\) 的。后者 \(O(n)\) 时间复杂度的。所以才会挂掉,2020luke 使用了后者并警钟长鸣。
再次科普:prev(it) 的作用是 \(it\) 这个迭代器往前一个位置。
link。
E
当你保存了一个版本,相当于暂停在此刻,然后我们可以开一个动态的数组,存储着第 \(i\) 个版本最后的点是什么,每一次更新到这个数组当中,然后存储一下网上跳是什么点,很显然可以大概建一个 \(fa_i\) 这样的数组,虽然代码中并不是这个名字,但是可以抽象理解。所以说:对于每一个版本让我们想到一种类似字典树的形式,虽然不一样,但感觉其实很像。差不多就是一个树来维护。
具体细节需要动态维护现在在这颗“树”上的哪一个点,然后实现起来比较简单,见代码:link。
*2024.1.10 ABC234 VP(OI赛制)
A
假递归,秒link。
B
享受暴力的快乐,秒link。
C
二进制拆位,然后是1就把他变成2,秒link。
D
其实一个优先队列即可,进来一个踢走一个,但是我想复杂了,用了set,因为每一次进来只有可能往后移或者不动,所以二分即可。秒link.
E
百年不见的 A 题水平的 E 题,直接暴力因为方案只有400多(有大佬算了)实际上最劣情况也就1000+,随便枚举,秒link。
F
赛时因为 F 罚坐 1h,我太菜。
以下是题解:
第一步:想到 Dp,毕竟方案数,百分之九十九都是 Dp。
第二步:思考一些问题,首先 \(s\) 这个字符串的顺序肯定不重要,毕竟重排和子序列,想到与随机取几个。所以说我们可以分类取,相当于就是计算这个字符取几个,另一个字符去几个,按顺序取,这么想会更好做。
第三步:先用桶存储出来每一个字符的数量。
第四步:考虑什么 Dp?想到计数 Dp。转移方程为 \(dp_{i,j}\) 代表选了前 \(i\) 个字母,长度为 \(j\)。
第五步:如何转移?\(dp_{i,j} = dp_{i,j} + dp_{i-1,j-k} \times C_j^k\)。此处的 \(C\) 为组合数。\(k\) 为这个字母取了多少个。理解一下为啥是这样:你如果不选这种字母,那么就是原来本身的贡献,如果选了,就是 \(dp_{i-1,j-k} \times C_j^k\),在之前的贡献转移过来要乘一个组合数,相当于要把这个 \(k\) 个字母放到最后对应的位置上,相当于是一个组合数来计算。
组合数我们可以通过 \(C_n^m = C_{n-1}^{m} + C_{n-1}^{m-1}\) 来转移,其实就是杨辉三角。因为 \(n \le 5000\) 所以 \(O(n^2)\) 时间复杂度可以通过,之所以我为什么不想题解区里人一样都用逆元啥的来搞,因为我数论菜的要死。。。
link。
G
确实有些难度,理解了一段时间。。
以下是题解:
转了一圈题解都不太清晰。来一篇详细的题解。
又是统计方案数,肯定是 Dp 啦!
设 \(dp_i\) 为前 \(i\) 个数分成若干段的价值。
那么转移方程就是 \(dp_i = \sum_{j=1}^{i-1} dp_j \times (\max_{k=j+1}^i a_k-\min_{k=j+1}^i a_k)\)。
也就是:\(\sum_{j=1}^{i-1} dp_j \times \max_{k=j+1}^i a_k - \sum_{j=1}^{i-1}dp_j \times\min_{k=j+1}^i a_k\)
此时的时间复杂度 \(O(n^2)\) 显然过不了。也就是说,必须把 $ \sum_{j=1}^{i-1} dp_j \times \max_{k=j+1}^i a_k - \sum_{j=1}^{i-1}dp_j \times\min_{k=j+1}^i a_k$ 这个式子控制在常数级以内。才可以通过此题。
所以考虑如何处理 \(\max_{k=j+1}^i a_k\sum_{j=1}^{i-1} dp_j \times \max_{k=j+1}^i a_k\) 和$ \sum_{j=1}^{i-1} dp_j \times \max_{k=j+1}^i a_k$。这两个子问题,很显然可以线段树,但是看了一圈题解区,好像没有那么愚蠢的做法。
引用教练灵魂画图:
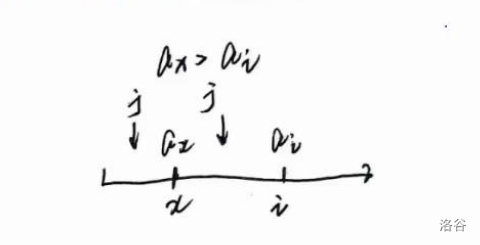
此时遍历到 \(i\)。上一段的末尾是 \(j\)。
我们设 \(x\) 表示的是 \(i\) 左边的点第一个大于 \(a_i\) 的位置,很显然我们可以得到两个式子:\(\max_{k=x+1}^i a_k = a_i\) 和 \(\max_{k=1}^x a_k > a_i\)。
先看取最大值:
那么我们可以对 \(j\) 进行分类讨论处理。
-
如果 \(j > x\),那么意味着 \(j\) 到 \(i\) 之前都是比 \(a_i\) 都小。所以最大值也就是 \(a_i\)。而此时当且仅当 \(j > x\),\(a_i\) 才是答案的贡献,而 \(x\) 是很好求的,单调栈维护即可。
-
如果 \(j \le x\)。问题就转换成如何求 \(j \le x\) 所能产生的贡献。这种情况我么可以设一个数组 \(f_i\) 表示 \(\sum_{j=1}^{i-1} dp_j \times \max_{k=j+1}^i a_k\)。所以又有 \(f_i = f_x + (\sum_{k=x}^{i-1}dp_k) \times a_i\)。
对此,我们可以用单调栈维护 \((\sum_{k=x}^{i-1}dp_k)\) 的值,进而可以维护 \(f_i = f_x + (\sum_{k=x}^{i-1}dp_k) \times a_i\) 的值。可以直接在单调栈中做加法和减法,所以不需要开一个数组,只需要变量即可。
注:最小值的方式也是类似的,只是单调栈的时候符号不一样,代码中最小值的变量是 \(g\)。
代码中的注释:
- (1)式为 \(f_i = f_x + (\sum_{k=x}^{i-1}dp_k) \times a_i\)。
- (2)式为 \(g_i = g_x + (\sum_{k=x}^{i-1}dp_k) \times a_i\)。
- (3)式为 \(dp_i = \sum_{j=1}^{i-1} dp_j \times \max_{k=j+1}^i a_k - \sum_{j=1}^{i-1}dp_j \times\min_{k=j+1}^i a_k\)。也就是 \(dp_i = f-g\)。
link。
2024.1.16 ABC336
A
link。
B
link。
C
这一道题,我们看到 \((0,2,4,6,8)\)。就想着是不是可以等效为 \((0,1,2,3,4)\)。
我们就想到可以用五进制来解决,因为第 \(n\) 个数可以理解为 \(n\) 转成五进制,但是发现第 \(1\) 个数为 \(0\)。所以我们将 \(n-1\) 转成五进制,然后直接每一位乘 \(2\) 即可。
link。
D
超级蒟蒻赛时没切,赛后发现一眼就是橙!偷偷查看Frank08代码。
相信很多人赛时想到了二分长度,然后单调队列,ST 表,线段树等做法,蒟蒻也是那么想,但是太复杂了,所以下面讲一种简单的方法,而且时间复杂度 \(O(n)\)。
我们可以贪心的想到,要把三角形数列的两端控制成 \(1\),然后向中间逐渐加一,是最优测率,更能使得他形成一个三角形数列,也就是最大化答案。
对于这个三角形数列,我们可以想成一个递增的和一个递减的,然后拼起来。
设 \(dp_i\) 为到第 \(i\) 个点最长上升的长度,如果此刻 \(a_i \le dp_{i-1}\)。那么代表到这个 \(a_i\) 无法延续以前有的最长上升,所以长度最多为 \(a_i\)。否则,长度继续累加。
后面累加也是同理。
link。
E
赛后发现其实不难。但是大家都说是蓝也,实际上是个 difficult 1538 的题,也不是很难的那种。
很显然是个 DP,或者打表。
但是记忆化搜索实现比较容易。
发现各个位数的累加和最多为一个常数,所以大概定到 \(140\)。
然后我们针对枚举位数的累加和逐个记忆化搜索。
在记忆化搜索的过程中,我们控制好每一位比 \(n\) 的对应那一位小,由于进位处理,如果之前的已经比他那一位小,我们直接就可以枚举到 \(9\) 了。否则,最多只能枚举到拆位后的 \(n\) 的那一位。
代码中的 \(t\) 变量,为此时状态算出来的值对 \(res\) 取模,\(res\) 就是位数的累加和。若 \(t=0\) 时就要记录答案。
然后到后面累计 dfs 下去的返回的值之和,然后进行状态转移。
F
这一题有四种操作,直接暴力枚举的话,时间复杂度是 \(O( 4 ^ {20})\)。很显然,可以 meet in the middle 来解决。所以可以优化到时间复杂度为 \(O(2 \times 4 ^ {10})\)。
对于记录答案和记录是否走过的数组都可以用 vector 和 map 来匹配实现。这样会更加方便,否则你手写哈希,虽然不是不可以,但是没必要呀。
对于每一个状态会有 \(4\) 种转移方式,然后我们发现了左上角是 \((i,j)\) 与 \((n-i,m-j)\),那么右上角就是 \((i,j+1)\) 与 \((n-i,m-j+1)\) 替换,由此我们由左上角延伸,四个操作都是 \(x\) 轴与 \(y\) 轴做了偏移量。跟方向数组类似,但其实我们发现了 \(0\) 到 \(3\) 二进制的特性,二进制的各个位正好可以对应偏移量。所以,我们对这个二进制进行操作就可以得到偏移量。然后在一个函数内,对这个状态进行转移。
注意,如果是奇数的行的话,还要换中间那一行的,记得判断。
代码中的实现,将每一个二维的坐标映射到了一维坐标上,这样就可以不用 vector 套 vector 那么麻烦了。
代码如下:有丰富注释!!
link。
*2024.1.18 ABC266(OI赛制)
A
秒link
B
秒link
C
比 G 还难,管理说橙最合适,抽象。。
怪我数学不好
这是我用老师的那个公式搞上去的:
这是我尝试用魔鬼三分然后找出高来求得,2023FJZ 一句:这有公式的。消愁
link(WA code)。别问为什么,调不出来呀
好好好过,不说了,这玩意就是靠你是否会数学,我不会 (逃~
D
赛时有点小差错赛后秒。
很显然是一个 Dp,因为位置只有五个,直接暴力转移就行咯,一开始初始话没有 -inf,后面又发现转移方程有点缺陷,再来又发现常数没开够。一句话总结:样例给了根给了一样。
link。
E
其实是期望 Dp,没学过有点怕,题有没读懂。后面发现转移直接 \(dp_i=max(j,dp_{i-1})\)。\(j\) 是 1 到 6,又是暴力转移,黄,没切,消愁
link。
F
赛时第一次 F 好吧,water,(老师稍作提醒)。。
首先,这里只有一个环,2020luke 叫:基环树!
然后对于环上每一个点往下染色,如果询问这两个点不同颜色,那么必定要上到环上,非简单路径,结束。
link。
G
以下是题解。切 G 太舒服了!!!
记录一下吧,虽然是 VP,但是我第一次想出 G 题!!
这个题目可能会想成一个 Dp,但是发现,这其实用组合数学求解即可。正好,教练刚讲了卢卡斯定理求解组合数,立马派上用场!!
我们可以稍微的转换一下题面:
一个 \(s\) 字符,你要构造出 \(R-k\) 个字符 r,\(G-k\) 个字符 g,\(B\) 个字符 b,\(k\) 个字符 k,因为 rg 肯定是单独出现的。
那我们现在就考虑如何用组合数来求解。
下文和代码默认将 \(R\) 和 \(G\) 减去 \(k\)。方便处理。
显然对于 \(R+G+B+k\) 个空给你填,r 肯定不能填到 g 前面,所以组合数是 \(C_{R+B+k}^R\)。
对于 g,g 肯定不能填到 r 后面,就是 \(C_{G+B+k}^G\)。
然后剩下只剩下 \(B+k\) 个空了,于是贡献是 \(C_{B+k}^B\)。剩下的都是 \(k\) 的了。
于是乘法原理得到答案是:\(C_{R+B+k}^R \times C_{G+B+k}^G \times C_{B+k}^B\)。
但是蒟蒻却调了一个多小时。
可能你也会有以下错误:
- \(R\) 和 \(G\) 没有减 \(k\)。
- 没有考虑到
g肯定不能填到r或r肯定不能填到g前面。
于是,你就轻松的过了一道蓝题!
link。
*2024.1.20 ABC242(OI赛制)
ABC 题逝世在死机的电脑上了,后面懒得写。。。
D
首先我们发现了,对于最终的答案是第 \(k\) 位,然而,每次进行一个操作相当于位置会乘 \(2\)。所以我们可以直接暴力,到了一定地方进行特判即可。直接模拟,从 \(k\) 位一直除 \(2\),(这是必然的)。然后若 \(k = 1\),以后肯定一直就是 \(1\) 了。我们又发现,他其实是一个长度为 \(3\) 的区间,直接将次数模 \(3\)。即可。
代码细节有一点多,详见代码。
link。
E
对于一个长度位 \(n\) 的回文串,我们只需要定位到前一半即可。
所以我们可以用递推来遍历一半的数组来得到答案。
设 \(dp_i\) 为前 \(i\) 个数的方案数。保证这些方案构造的都是小于 \(s\) 串的。
于是我们显然可以得到 \(dp_i = 26 \times dp_{i-1} + tmp - 1\)。
\(tmp\) 为 \(s_i\) 是第几个字母。
\(26 \times dp_{i-1}\) 显然是之前的方案,然后此时每一种字母都可以填,所以直接乘法原理。
\(tmp - 1\) 是之前的部分都是等于 \(s\) 的,到这一位有多少种方案是可以使得他保持小于 \(s\) 串。
到了最后,考虑你要是 \(s\) 的前一半构成的一个回文串比 \(s\) 小,这也是一种可行方案,答案增加一个。
link。
F
我们先预处理以下 \(b\) 数组和 \(w\) 数组。
这两个数组的定义如下:
- \(b_{i,j}\) 代表将输入的 \(B\) 个点放入 \(i\) 行 \(j\) 列的方案数。
- \(w_{i,j}\) 代表将输入的 \(W\) 个点放入 \(i\) 行 \(j\) 列的方案数。
如何求 \(b\) 数组?
首先很容易想到,所有的方案数是 \(C_{i\times j}^B\)。但这不一定填满了 \(i\) 行 \(j\) 列,所以还需要减去一部分的方案数。
如果这 \(i\) 行 \(j\) 列是只有 \(x\) 行 \(y\) 列实际有作用的话,方案数是 \(C_i^x \times C_j^y \times b_{x,y}\)。于是我们直接枚举 \(O(N^2 \times M^2)\) 来进行转移。
但要注意的点是 \(i=x\) 和 \(j=y\) 同时满足时是不可以减去的。因为这其实就是答案的贡献,减去了,就没有了。
对于 \(w\) 数组也是一样的道理。
那我们知道了这两个数组又能干啥呢?
很显然,最后的答案等于:\(\sum_{i=1}^n \sum_{j=1}^m \sum_{x=1}^{n-i} \sum_{y=1}^{m-j} C_n^i \times C_m^j \times C_{n-i}^x \times C_{m-j}^y \times b_{i,j} \times w_{x,y}\)。
其中 \(C\) 是组合数,我们先用递推的方式预处理即可。
*2024.2.28 ABC238 VP(OI赛制)
A
赛时没过简直小丑。没有特判 \(1\) 的情况,痛失A题。。link。
B
我们对于每一个点做一个累加值,可以理解为到这个点已经累加了多少度了,同时判断大于等于 \(360\) 的时候要减 \(360\),然后在一个 \(vis\) 数组上标记即可。我怕有点问题,还破环成链了,但好像也不需要。link。
C
这一题显然是需要找一些规律。先把 \(n\) 的位数求出来,然后逐个去枚举,然后会发现对于 \(i\) 位数的都是一个等差数列,乘法一下即可,由于会炸,所以mod勤快一些。时间复杂度 \(O(\log_{10} n)\) link.
D
这一题要找两个数 AND 等于 \(x\),那么这两个数必须大于等于 \(2x\)。因为这两个数与 \(x\) 与都是 \(1\),所以每一个数至少是 \(x\)。我本以为到这里便结束了。实际上你还需要判断 \((y-2 \times x) AND x ==0\)。这要保证的是,除了最基础要有 \(2x\),此外的数拆成二进制,必定是放在其中一个数上面,另一个数没有(显然,因为如果两个同时有,那么 AND 就变了。)但是还得保证这些数的每一个二进制位于 \(x\) 是不重合的。因为这才可以使得有空余的位置填进去。link。
E
第一眼:线段树,第二眼:区间 DP,好吧,没有第三眼了。其实这题就是一个并查集,很巧妙,咋就没想到?要得出一个区间,必定是有无缝连接的各个子区间合起来,这时候我们就可以利用并查集。给出 \(l\) 与 \(r\),这个区间就可以拼接到 \([x,l-1]\) 的后面,然后就可以得出新的一个区间,\(x\) 我们不知道,也不需要知道。我们就可以直接将 \(r\) 点堆进 \(l-1\) 这个并查集内部,显然他们属于一个并查集,因为他们都是一样的共同的一串已知的区间。然而,答案是啥?显然,如果 \(0\) 和 \(n\) 在一个区间了,那么,这就是可以从头连到尾的区间,输出 Yes,结束。 link。
F
思维比E简单吧,实现可能比E难一些,但却是来说,差不多。\(n\) 是 \(300\) 级别,送给你的是 \(O(n^3)\) 时间复杂度的解法,考虑 Dp,我们可以先按照 \(a\) 这一维度排序,然后就只用考虑 \(b\) 这边了。\(dp_{i,j,x}\) 代表的是考虑到第 \(i\) 个点,选了 \(j\) 人了,此时未选择的人中 \(b_i\) 最小是 \(x\)。转移的方式是:如果可以新加入人:\(dp_{i+1,j+1,x} += dp_{i,j,x}\)。不加人:\(dp_{i+1,j,\min(x,b_{i+1})} += dp_{i,j,k}\)。最后的答案是 \(\sum_{i=0}^{n+1} dp_{n,k,i}\)。状态表示中写了 \(b_i\) 但实际上排序的需要,我们可以开一个 pair 来解决。link。
*2024.2.29 ABC217 VP(OI赛制)
A
water problem link。
B
water problem link
C
water problem link
D
water problem 维护两个set,一个正一个负,跑两次Lower bound确定左端点和右端点即可,我用的是左闭右闭,注意set用自带的Lower bound,这次2023FJZ又被卡了,上次是luke。。ohhlink。
E
water problem ABCDE联合water是吧?。每一次加入放进一个 queue 里,此时无序的,如果要排序,堆进一个 priority queue,如果 priority queue 没有元素,那么取得第一个便是 queue,反之,则取 priority queue。link
F
开始上难度,有意思的一题。感觉,根 23 年提高组消消乐有那么一点像,就是区间 Dp,类似括号匹配。但是这种题容易算重,所以我们需要保证每次转移都添加元素。对于一个区间 \([l,r]\),我们可以从 \([l+1,x-1]\) 和 \([x+1,r]\) 转移来,保证每次 \(l\) 与 \(x\) 是可以匹配,然后消除。\(x\) 是区间 Dp 中断点。然后还需要乘一个组合数,那就是 \(C_{\tfrac{x-l-1}{2}+1+\tfrac{r-x}{2}}^{\tfrac{r-x}{2}}\)。就是你选择这两段拼接起来的先后顺序。
于是,如果 \(l\) 与 \(x\) 匹配,那么可以得到转移:\(dp_{l,r} = dp_{l+1,x-1} \times dp_{x+1,r} \times C_{\tfrac{x-l-1}{2}+1+\tfrac{r-x}{2}}^{\tfrac{r-x}{2}}\)。结束。link。
G
这道题的 Dp 转移基于一个叫做斯特林数的东西。\(dp_{i,j}\) 代表的是前 \(i\) 个数,分成了 \(j\) 组。对于两种情况:新加入一个组,那么是 \(dp_{i,j} = dp_{i-1,j-1}\)。不加入:\(dp_{i,j}\) 加上贡献 \(dp_{i-1,j} \times (j- \tfrac{i-1}{m})\)。\(j- \tfrac{i-1}{m}\) 代表的是他可以放的组别的个数。比较容易理解,按照这样转移即可。link。
*2024 3 10 ABC219 VP(OI赛制)
欣赏一下,两页提交记录的我link。说来也有点抽象,不知道为什么几乎每一道题都不是1A。
这一次复盘应该是写的最多的一次,码字码了两个多小时,总共 \(4869\) 字。
如果我语文作文能够写那么多那就很好了。。。
A
water problem link。
B
water proble link
C
判断字典序的方式有误link。
D
考虑 DP,这是一个典型的背包拓展,每一个物品只能选一个。
我们 \(dp_{i,j,k}\) 的定义为前 \(i\) 个物品,重量 \(j\) 的章鱼烧,重量为 \(k\) 的太白烧。
因此可以得到转移方程 \(dp_{i+1,j+a_{i+1},k+b_{i+1}} = \min(dp_{i+1,j+a_{i+1},k+b_{i+1}},dp_{i,j,k})\) 和 \(dp_{i+1,j,k} = dp_{i,j,k}\)。
这两个分别为选或者不选。
VP 赛时 WA:link。
思路大体上是对的,挂在了没有初始化,而且还可以有一定的优化,就是我们当这个背包的容量已经大于 \(x\) 我们可以直接将此时的容量设为 \(x\),可以有效减低空间代价,对于另一个背包也是取 \(\min(val,y)\)。\(val\) 是此刻的背包重量。
因此选的转移方程变成了 \(dp_{i+1,\min(j+a_{i+1},x),\min(k+b_{i+1},y)} = \min(dp_{i+1,\min(j+a_{i+1},x),\min(k+b_{i+1},y)},dp_{i,j,k})\)
初始化一下,将 \(j\) 为 \(0\) 和 \(k\) 为 \(0\) 的状态都设为 \(0\)。其他的都是无穷大。
最后的答案就是 \(dp_{n,x,y}\)。
AC 的代码:link。
E
一开始想到的是如何设计状压,是枚举护城河所在的点还是所在的边呢?思考着通过枚举护城河所在位置,推出有多少符合条件,显然,枚举点,很难算出有多少可能,枚举边,也是比较难算。
但是,正难则反,所以,我们直接状压哪些点被护城河包含着,那么,这显然对应着一个护城河的方案,我们只需要在判断一下是不是所有的村庄都在状压的点内,而且,这个方案能够形成唯一一条护城河。
难点就在这个方案能够形成唯一一条护城河,稍微画个图思考,就知道,如下两种不符合方案:
- 如果一个不是状压枚举的点被一堆状压枚举的点所包围,那么这个方案就不合法。为什么呢,因为这样类似一个环,里面要一圈护城河,外面要一圈护城河,两条,不符合方案。
- 如果状压枚举的点不连通,那么,不符合方案。
这样,我们就可以用洪水填充法。找一个是状压枚举的点,对它的连通块染色,注意,此时染色的只能是状压枚举的点。然后我们再找一个非状压枚举的点,对他的连通块染不同的色,此时也是只能染非状压枚举的点。然后我们再遍历所有的点,如果这个点没有被染色,要么就是非状压枚举的点被分成了多个连通块(也就是被包含的情况),或者是状压枚举的点被分成了多个连通块。
但是,我们发现这样做,有点小问题。
看看这组样例:
1 1 1 1
1 1 1 1
1 1 1 1
1 0 1 0
显然,这是有 \(4\) 种方案,但是,你的代码会算出来 \(3\)。为啥?因为你的代码把最下面一行的 \(0\) 判断成两个不同的连通块,但是,实际上他们可以同时包含的。
如果我们把图扩建:
0 0 0 0 0 0
0 1 1 1 1 0
0 1 1 1 1 0
0 1 1 1 1 0
0 1 0 1 0 0
0 0 0 0 0 0
外面套一圈 \(0\),那么问题就解决了,下面的 \(0\) 就可以是一个连通块了。
我们只需要把搜索的范围控制在 \(([0,5],[0,5])\) 中即可。
我在深夜的时候寻找 2020luke 同学进行调代码:link。
这一份代码我们两个人都没有发现问题,就睡觉了。实际上,那是个不起眼的错误,第二天早上发现了之后只能说是堂食。
为什么呢?
我枚举了 \(x\) 和 \(y\) 轴,两重循环,而在 dfs 搜索之后仅仅是一个 break,他仅仅是推出了一个维度的循环啊。并没有将两个循环同时推出掉。非常堂食。所以在第二天早上,我把循环里面加了个标记的变量,方便直接推出两层循环,这样就直接 AC 了。如果遇到这种错误,确实也比较难看出来。
AC 的代码:link。
F
我们先把第一轮中每一个点的点处理出来。变成一个 pair 数组。
如下图:
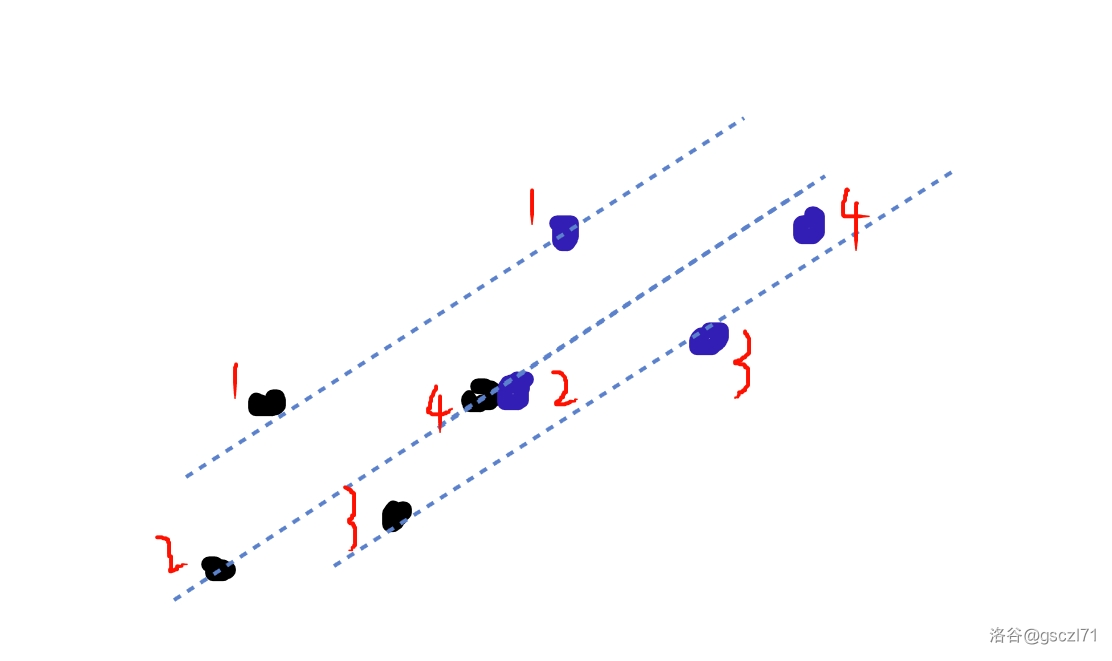
黑色点是原始的点。
我们设一开始第一个点为 \((0,0)\),然后最后一个点为 \((dx,dy)\)。那么我们就可以发现对于每一轮,他们之间的差都是一个固定的偏移量,偏移量是 \((dx,dy)\),也就是第 \(i\) 轮的最后一个点是 \((dx \times i,dy \times i)\)。
如果这个点第一次出现是在 \((x,y)\)。那么他后面对应的 \((x+(i-1) \times dx,y + (i-1)\times dy)\)。
图中只画了两轮。
第二轮便是蓝色的点。
分别对应着他们的编号。
由于每一个点下一轮的偏移量都是相同的,于是,我们发现对于这个点,之后都是形成了一个斜率为 \(\dfrac{dx}{dy}\) 的一条直线。然后我们只需要对每一条斜线上去判断。
由于所有的线都是斜率相同,所以不用考虑斜率,将他(斜率)默认为 \(\dfrac{dx}{dy}\) 即可。
我们课以将每一块(相当于每轮的区域)切割出来,如下图,被切成了若干块。
每一个点在不同轮数中在他们自己对应的块内相对位置都是相同的。
例如点 \(3\) 在它的那一块的相对位置,就是两个箭头所指向。也就是对于他们这个块内第一个出现的点的位置偏移量都是一样的。
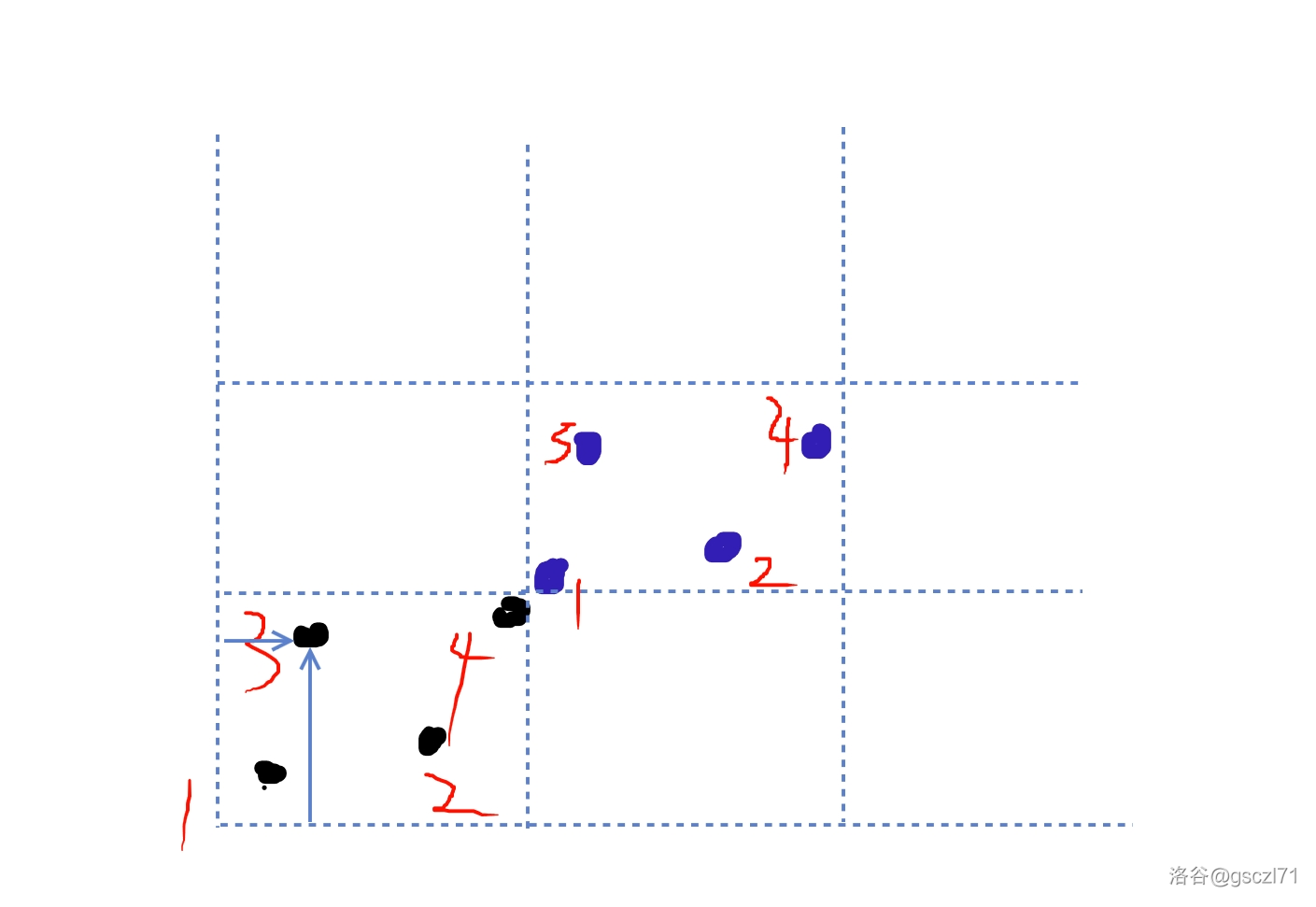
对于 \((x,y)\) 他所在的斜线就是编号为 $(x \mod dx,y - b \times \left\lfloor\dfrac{x}{dx}\right\rfloor $ 的斜线上,也就是 \((x \mod dx,y - dy \times \dfrac{x-x \mod dx}{dx}\)(注意,这个编号是有两个数值,你可以开一个 pair 来作为映射的键)。
因为,重复,仅仅有可能是一条斜线上重复,不可能是,另一条直线上与这条直线重复,毕竟两条斜率相同的直线不可能是有交点,必须是平行的,不然他们就不是斜率相同的。
所以我们只需要针对相同编号的数,进行计算,相同编号,代表着,就是在一条直线上。
所以我们对于每一个 \((x,y)\)。将编号为 \((x \mod dx,y - b \times \dfrac{x-x \mod dx}{dx}\) 的直线,存储一下 \(\left\lfloor\dfrac{x}{dx}\right\rfloor\),\(\left\lfloor\dfrac{x}{dx}\right\rfloor\) 代表什么呢?代表的就是这个点所在块的编号。
很显然,对于直线上所有点的块编号,去重排序后,第 \(i\) 个和第 \(i-1\) 个只差,都是他们之间会出现的个数,注意,有可能会大于 \(k\),这显然不可能,因为最多 \(k\) 轮。还要与 \(k\) 取最小值。
假设这个编号内所有点的块编号都存在了 \(v\) 数组中,那么答案要加上 \(\sum \min(k,v_i - v_{i-1})\)。
时间复杂度是 \(O(n \log n)\)。
代码实现中还有一些细节。
-
由于所有的编号都得要排序和去重,所以我们选额开 set 来存储。
-
如果 \(dx\) 和 \(dy\) 都是 \(0\),我们可以直接把一开始统计的数量(去重后)输出。
-
如果 \(dx\) 是 \(0\),那么他就不能做除数,所以我们要交换一下 \(dx\) 和 \(dy\),是没有区别的,只不过是相当于把整个图旋转了一下。(旋转后的 \(dx\) 不可能 \(0\),因为如果 \(dx\) 和 \(dy\) 都等于 \(0\),那么就直接被之前的条件判掉了)。所有的点也得交换一下。
-
如果 \(dx < 0\),那么也不好搞,所以把他换成整数,对应的所有存储的坐标也是乘个 \(-1\)。
-
取模记得注意负数情况。
AC 的代码:link。
G
这道题最暴力的方案,就是每一个询问,然后往外扩散,但如果是一个菊花图,那么就会被卡到 \(O(qm)\)。显然是不行的。
首先 \(O(q)\) 这个是免不了的,只能从优化 \(O(m)\) 入手。我们是不是可以根号分治?对于这个点连边小于 \(\sqrt(n)\),我们可以直接把暴力去处理,然后如果大于,那么就不管了。
这里的不管,实际上类似线段树上的懒标记,等到要用的时候再来更新,正是线段树的精髓,也是这道题最重要,最巧妙的一点。
下面讲一下代码实现的流程。
先把所有的边数大于等于 \(\sqrt n\) 的点预处理出来,最多也只有 \(\sqrt n\) 个这样的点,时间和空间代价不大。
再预处理一下每一个点所能到达那些这些重点,存在 vector 里,重点,代表的是边数大于等于 \(\sqrt n\) 的点。
我们在每一次操作之前先 update 一下这个点,可以理解为线段树中的 pushdown,将标记下沉,或者是将标记更新。
更新里面,我们只需要访问这个点预处理的 vector,也就是所连向的重点,最多只有 \(\sqrt n\) 个。
如果这个点是轻点,也就是边数小于 \(\sqrt n\) 的点,那么还需要 \(\sqrt n\) 的暴力枚举转移。
到了最后,我们再把每一个点更新一遍。
所以,总的时间复杂度是 \(O(m + q \sqrt n + n \sqrt n)\)。
分别为,预处理,询问过程,最后更新。
AC 代码:link。
2024 3 10 ABC337
C
这道题告诉你的是对于每一个点他前面那个点是啥,所以你直接做一个链表的结构。
然后记录这个点后面是哪一个点,然后从第一个点往后一直更新指针,最后到达结尾。
如何记录这个点后一个点是啥?那么对于每一个 \(a_i\),开一个 \(vis\) 数组,\(vis_{a_i} = i\)。这样就完成了操作。
然后记录下 \(a_i = -1\) 的那个点,然后设 \(x=i\)。
每一次就是 \(x= vis_x\) 往后跳,就是割链表结构。
考察的是你对链表熟不熟悉。
link。
D
这道题只有两种方式:竖着和横着。
所以我们对两种方式分讨。
先说竖着。
我们从上往下遍历,开两个指针,一个是遍历的 \(i\),另一个是往回走最远的指针 \(j\)。\(i\) 到 \(j\) 的这段区间中不会包含 x。如果碰到了 x,那么我们就要将 \(j = i+ 1\),要保证区间内不包含 x。若当 \(i\) 到 \(j\) 的长度等于 \(k\),此时就可以通过将 . 换成 o。
我们只需要在双指针移动的时候统计以下区间内 . 的数量,然后在符合条件的时更新答案。
横着也是同理,只需要横着遍历,具体细节也是一样的。
注意细节。
link。
2024 3 10 ABC339
C
问你,全程要人数非负,然而最后的人数最少。
首先,我们得维护一个 \(sum\),统计此时相对于一开始已经有多少人的变化,也就是多了多少或者少了多少。
我们开一个 \(ans\) 为每个时刻 \(sum\) 值的最小值。
如果 \(ans\) 为负数,那么代表对于一开始已经少了 \(-ans\) 了。为了保证非负,所以一开始就设置为 \(-ans\),若 \(ans\) 非负,那么一开始 \(0\) 个人也可以的。
所以答案就是,一开始的人数与最后一刻的 \(sum\) 之和。
link。
D
我们叫两个玩家为 \(A\) 和 \(B\),设状态 \((a,b,c,d)\) 为 \(A\) 在 \((a,b)\) 下标,\(B\) 在 \((c,d)\) 下标时的最短路。我们单独判断 \(A\) 和 \(B\) 分别是否可以走,不可以走的话,就继承之前的点,否则就继续移动。按照这个方法,直接跑 Dij 暴力过去即可。就转移稍微分类讨论一下,其他的都是一样的最短路写法。
时间复杂度应该是 \(O(n^4 \log n)\),对于 \(n\) 那么小几乎不用考虑时间复杂度了。
https://atcoder.jp/contests/abc339/submissions/49987794。
E
这是重题!
这种题显然是 dp,不太可能是贪心。因为你想,咋贪呢?
设一个转移方程 \(dp_i\) 从 \(dp_j\) 转移,并且 \(a_i\) 和 \(a_j\) 的差小于等于 \(d\)。
时间复杂度 \(O(n^2)\)。
出题人非常善良的,给了一个 \(a_i \le 5\times 10^5\)。那我们是不是在每一次转移后,记录一下这个最长的子序列,大概就是 \(vis_{a_i} = \max(vis_{a_i},dp_i)\)。这样,我们每一次转移的时候只需要遍历 \(vis_{a_i-d}\) 到 \(vis_{a_i+d}\) 取一个最大值,进行转移,然后再更新。
时间复杂度稍微优化了,\(O(n \times d)\)。但显然还是和 \(O(n^2)\) 没啥区别。
再回想,我们是从 \(vis_{a_i-d}\) 到 \(vis_{a_i+d}\) 取一个最大值。对?线段树!
线段树可以在 \(O(\log n)\) 的时间内进行区间最大值查询,修改也是一样的时间复杂度。那么,我们搬运过来线段树 1 的板子,然后稍作修改即可!
时间复杂度是 \(O(n\log n)\)。
link。
F
当我在尝试我能过都少个点的时候。。AC!
这题大抵上是得用到哈希的了,具体是几哈希,看就是数据水不水了,结果数据不水!甚至弱到爆!
接下来我讲讲我玄学地单哈希做法!
我们将每一个输入进来的字符串哈希一下,存到 \(a\) 数组中,大概也就是自然的保留了后面一些位数,然后将这个哈希值放入一个 map 里,名为 \(mp\),记录同样的哈希值有多少个。
接下来就是 \(O(n^2)\) 枚举,答案就加上 \(mp_{a_i \times a_j}\)。
但是自然溢出会炸!
我们得取一个靠谱的模数。
于是我取了 \(11451419198101111\) 这个数,竟然过了。
虽然有些玄学地成分,但是还是可以过的,证明,这玩意基本上应该也是对的 AT 数据水了。
link。
2024 3 10 ABC340
C
这一题有两种做法:记忆化搜索,或者打表找规律。
首先,我们把暴力写出来,表格如下:
1 0
2 2
3 5
4 8
5 12
6 16
7 20
8 24
9 29
10 34
11 39
12 44
13 49
14 54
15 59
16 64
17 70
18 76
19 82
20 88
前面是 \(n\),后面的是答案。
有没有发现什么,仔细看看,发现它们之间的差都是比较小的,我们再把差列举做出来。
2
3
3
4
4
4
4
5
5
5
5
5
5
5
5
其实差可以分为 \(\log n\) 段,第 \(i\) 段的长度为 \(2^i\)(\(i\) 是从 \(0\) 开始的)。然后第 \(i\) 段的公差是 \(i+2\),因此,我们可以直接 \(O(\log n)\) 模拟即可。
对于这样做的证明,我还是不太会,但是在比赛的时候只要你 AC 了,那就行,如果有大佬可以讲讲如何证明,可以在评论区留言。谢谢!
code。
D
这道题,他说,可以从 \(i\) 到 \(i+1\) 贡献为 \(a_i\),然后,\(i\) 到 \(x_i\) 贡献为 \(b_i\),一开始还想着将 \(x\) 反着映射一下,然后 Dp,但是我们发现样例中有 \(x_i \le i\) 的,Dp 无法做到有后效性。
所以我们可以连边 \((u,v,w)\),对于 \(i\) 可以连 \((i,i+1,a_i)\) 和 \((i,x_i,b_i)\)。这样,边有 \(2\times n\),直接跑最短路即可,用的 Dij,所以时间复杂度是 \(O(n\log n)\)。
code。
E
遇到这种区间的题目,想都别想,直接上线段树。
列举一下,发现其实是可以分为这两种情况:
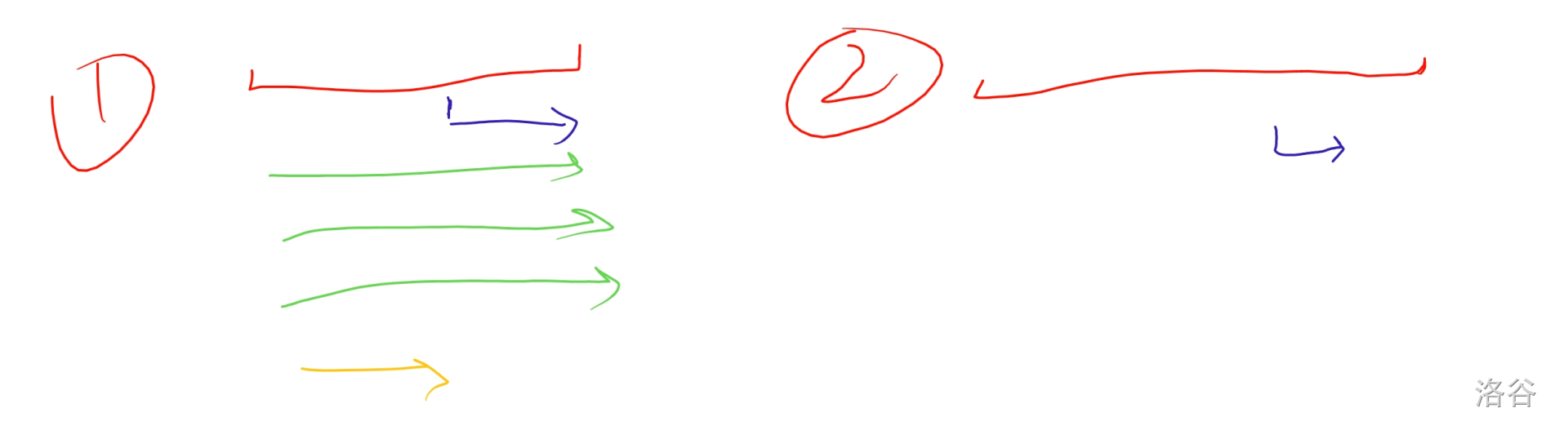
先看第二种情况。那么就是 \(a_i \le n-i\)。也就是往后填就不会跳到前面来。
第一种情况呢,就是 \(a_i > n-i\)。
分成三个部分进行线段树的区间修改,第一个区间是 \(i+1\) 到 \(n\),这里加一,也就是蓝色的线段。然后是 \(1\) 到 \(n\),这里要加除了第一个区间用掉的再除以 \(n\) 向下取整,也就是还能有多少个来回,很显然,如图,就是有 \(3\) 次,因为有三条绿线。而且都是 \(1\) 到 \(n\) 的线段。然后 \(n\) 剩下的数就是黄色的线段。
细节还要注意下,例如第一段如果 \(i=n\) 的时候是没有的,要排除掉,然后第三条一定是 \(n\) 不等于 \(0\) 才可以,不然就出现了一个区间 \(l > r\)。
code。
2024 3 10 ABC341
C
由于发现数据范围较小,所以我们可以枚举起始点,然后按照输入字符串的步骤一个个走即可,如果遇到了海,那么返回 false,否则,到最后这就是一个 true,那么贡献增加,时间复杂度是 \(O(HWN)\)。
2024 3 10 ABC342
G
连续一个月都是线段树。。
赛后发现 G 水啊。赛时却卡着最后两分钟把 D 赶出来,是的,确实 C 题 D 题有点令人恶心。
来讲讲这次 G 为啥水。
显然,这是一个数据结构题,我们想想可以用线段树来维护。
有一个操作对区间内的每一个 \(a_i\) 都变成 \(\max(a_i,x)\),很容易想到,对于点 \(a_i\),最后查询的时候改变它的一定是这些修改操作中最大的 \(x\)。因此,我们可以对线段树上每一个点里维护一个 set,用来记录的是这些 \(x\)。
对于撤回操作,我们也可以开一个 set 来维护,记录的是哪些数删除。到了查询的过程中,对之前的操作进行删除即可。
2024 3 10 ABC343
G
第一次赛时秒 G!!!(鼓掌。。
这题其实很简单。
我们看到 \(n \le 20\),那是什么?状压 Dp。没错。考虑如何转移呢?
应该说如果状态里已经有了 \(i\) 这个字符串,我们还有一个字符串 \(j\),该如何转移进去呢?
那我们分两种情概况:
- 字符串 \(s_j\) 完全在 \(s_i\) 中,我们可以不用增加代价的转移,为了实现,我们需要预处理每两个字符串是否互相包含,用 KMP 来预处理。
- \(s_j\) 要拼在 \(s_i\) 后面,我们要重合尽可能多,才能保证长度尽可能小,所以我们可以算出这两个字符串的最长公共前后缀,这是什么?对,KMP 的 next 数组!也是预处理得出来。如果我们要看 \(s_j\) 拼在 \(s_i\) 后面的最长前后缀,那么我们将 \(s_j\) 在前,\(s_i\) 在后(
我没有写错,就应该反着拼),然后拼接成新的字符串,去跑 KMP 用的那个 next 数组。注意,这个字符串的最长公共前后缀必须要小于两个字符串分别的长度。我们就不停的往回跳,直到符合长度。这是 KMP 算法的精髓,就是不断找次长的最长公共前后缀。不懂的看这 link。这样,我们就可以算出 \(s_j\) 要拼在 \(s_i\) 后面,最长重合多少。
这样,我们就可以直接状压 DP 解决。按照上述两种情况转移。
\(len\) 是字符串长度 \(2 \times 10^5\)。
预处理时间复杂度 \(O(n^2 \times len)\)。
状压是 \(O(n \times 2^n)\)。乍一看像是 \(O(n^2 \times 2^n)\),实际上其中一个 \(O(n)\) 的时间复杂度是拆位状态,判断这一位有没有,但这个可以约做常数,仅仅是给时间复杂度中 \(2^n\) 的指数增加一个小常数,完全可以忽略。
code。
*2024 3 13 ABC243(OI赛制)
A
water link.
B
waterlink
C
贪心一下,去一下每一个 y 轴上向右的最小值,向左的最大值,贪心策略,若最小值小于最大值,代表可以碰到,否则没有其他可能。
link。
D
显然,如果直接暴力去做,显然会炸,或许高精度是可以的?
但是,我们有更巧妙的方式。
因为题目说了,保证最后的答案在 long long 范围。我们发现往上走和往下走以互相消除的,所以我们只需要保证每一次操作都是往下走,那就不会炸。所以我们可以维护一个栈,然后对于一个往上走的操作,我们就把栈顶(往下走)的操作抵消掉,类似于括号匹配。这样就可以成功消除所以的往上走。但是,如果此时栈顶为空咋办?很好办,我们直接暴力把此时的位置除以 \(2\)。等到最后,栈里面只有一堆往左还是往右的数,所以,直接往下暴力的跳即可。
link。
E
很巧妙的一题,Floyd 好题,很像一道叫做:重要的城市 的题。
我一开始思考的是,对于每一次 Floyd 转移成功的时候用一个 \(vis_{i,j} = k\) 来记录,然后到后面在逐个递归往前推,后面发现其实是有反例的。
所以,我们考虑直接跑一边 Floyd 板子。对于 \(dis{i,j} = dis_{i,k} + dis{k,j}\) 的情况,直接记录一下答案,即可。由于举不出反例所以这是正解。
当然,仔细想想,这肯定是对的。主函数代码超过 \(5\) 行的都是没有练习过压行的。
link。
F
这是一个概率 Dp。
我们可以先预处理一下抽到每一个 \(i\) 的概率是多少,即:\(\frac{W_i}{\sum_{j=1}^{n}W_j}\)。
\(dp_{i,j,k}\) 表示前 \(i\) 个角色,抽了 \(j\) 个,\(k\) 种不同的角色。
每一次转移的时候都是对第 \(i\) 个进行转移,对于这个 \(i\),它的概率是 \(p_i^x\)。\(x\) 为抽的个数。
由于 \(x\) 可以遍布于之前 \(j\) 个中,于是还需要乘上一个组合数:\(C_j^x\)。
于是我们可以得到 Dp 状态转移方程。
\(dp_{i,j,k} = \sum_{x=1}^j dp_{i-1,j-x,k-1} \times p_i^x \times C_j^x\)。
最后的答案就是 \(dp_{n,K,m}\)。
我们可以先预处理一下组合数,就是杨辉三角。
注意,由于有除法,所以需要使用逆元,记得勤取模。
link。
G
很容易想到,我们可以 Dp,\(dp_i\) 代表以 \(i\) 结尾,那么 \(dp_i = \sum_{j=1}^{\sqrt i} dp_j\)。
时间复杂度是 \(O(x \times \sqrt x)\)。
由于 \(x\) 很大,所以显然是时间复杂度承受不了的,考虑如何优化这个 Dp。
对于之前的状态 \(dp_i = \sum_{j=1}^{\sqrt i} dp_j\),\(j\) 对 \(i\) 有影响,当且仅当 \(j \le \sqrt i\)。
那如果又有 \(dp_j = \sum_{k=1}^{\sqrt j} dp_k\),\(k\) 对 \(j\) 有影响,当且仅当 \(k \le \sqrt j\)。
那么因此推出当且仅当 \(k \le \sqrt{\sqrt i}\) 的时候,\(k\) 才对 \(i\) 有影响。
我们考虑能不能把上述 \(k\) 范围内的所有 dp 按照之前的公式直接暴力转移,然后对于一个询问 \(x\),我们直接计算对应的 \(k\) 的贡献。\(k\) 的贡献便是 \(\sqrt{\sqrt x}\),所以说值域最多也不到 \(10^5\),直接暴力即可。
然后对于每一次询问,以 \(\sqrt {\sqrt x}\) 的时间复杂度统计答案,统计答案就是对于你枚举的每一个 \(k\),然后判断他能对 \(x\) 产生的贡献,最后累加即可。
link。
*2024.3.21 ABC221 VP(OI赛制)
A
water link
B
water link
C
water link
贪心的取,肯定最大放前面,然后尽量让两个数平均即可
D
直接差分然后前缀和即可,由于 \(a_i \le 10^9\) 所以需要离散化一下。
对于每一个点差分值是 \(1\) 或者 \(-1\)。
对于每一个点和上一个点之间的距离都是上一个点的值。
所以在统计的时候要乘上这个区间长度。
link。
E
我们只需要关心子区间的左端点和右端点怎么选,然后中间的随便选。
所以我们可以得到答案为 \(\sum_{i=1}^{n-1} \sum_{j-i}^{n} [a_i \le a_j] \times 2^{i-j-1}\)。$ [a_i \le a_j] $ 代表的是一个布尔值,可以理解为如果 \(a_i \le a_j\) 才需要加上 \(2^{i-j-1}\)。
直接求这个式子的时间复杂度是 \(O(n^2 \log n)\)。(因为快速幂时间复杂度是 \(\log n\),当然你可以直接位移,就是 \(O(1)\),但时间复杂度依然是 \(O(n^2)\) 及以上。还是需要优化。)
我们对这个式子进行一些转换:
$\sum_{i=1}^{n-1} \sum_{j=i+1}^{n} [a_i \le a_j] \times 2^{i-j-1} $
\(= \sum_{i=1}^{n-1} (\sum_{j=i+1}^{n} 2^{-i-1} \times [a_i \le a_j] \times 2^{j})\)
\(= \sum_{i=1}^{n-1} ( 2^{-i-1} \times \sum_{j=i+1}^{n} [a_i \le a_j] \times 2^{j})\)
然后对于 \(\sum_{j=i+1}^{n} [a_i \le a_j] \times 2^{j}\) 我们可以直接用数据结构来维护,这里用的是树状数组。
link。
F
本题要引入一个知识点,就是树的中心。
因为我们每一次选的集合,每两个点都构成一条直径。我们发现,如果直径上有 \(k\) 个点,那么如果 \(k\) 是奇数,那么所有直径都穿过这个中心,如果它为偶数,那么会有两个中心,那么这个直径会穿过两个中心之间的边。
所以,奇偶处理的方式就不同,得要进行分讨。
先放一个图:
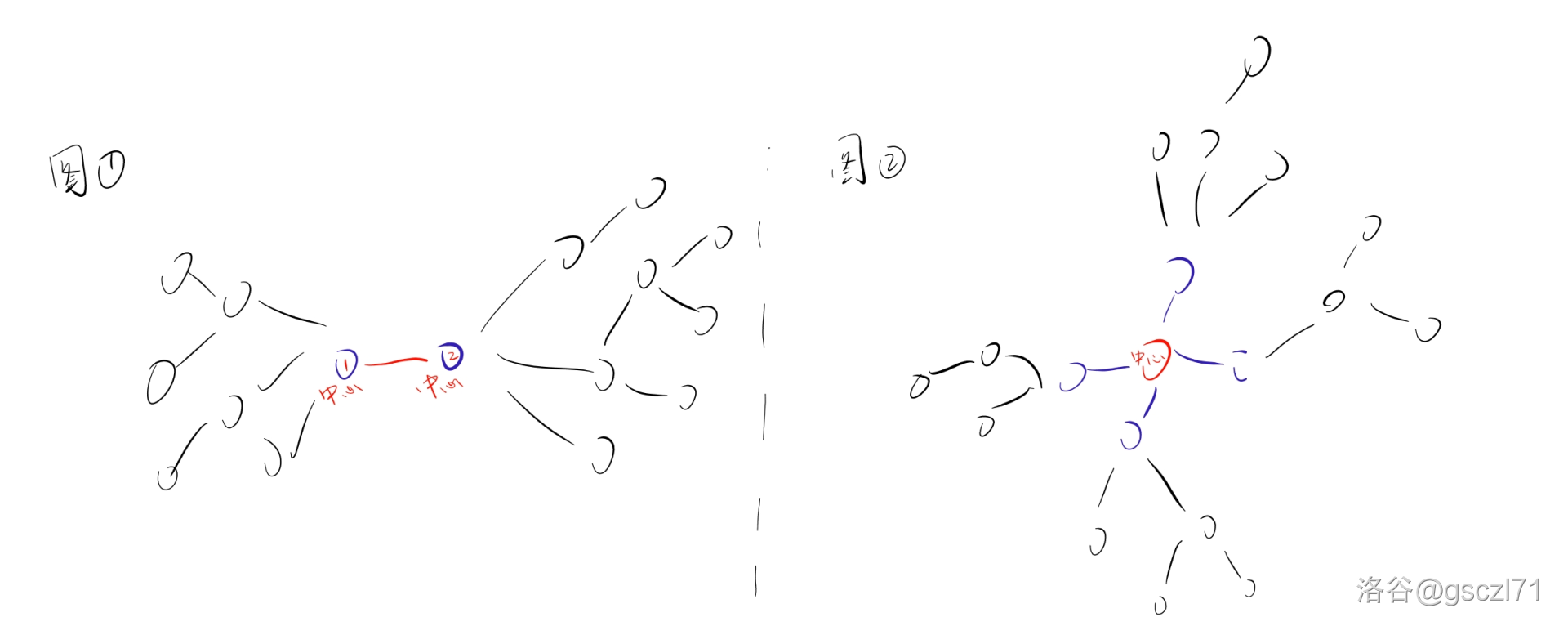
奇数情况(如图二):
- 红色的点为单个的树的中心,所有蓝色节点就是直接它的儿子。我们选两个端点作为直径的两端点,显然不能在都在同一个蓝色节点的子树内,如果两个点在同一个蓝色节点的子树内,那么,显然会有更短的方案(他们连的蓝色的点然后就连回去了)。所以,我们选的两两个点,都不能出现在同一个子树内。于是,我们可以统计每一个蓝色节点的子树内有多少个是有直径长度的一半,这样,将所有数量乘法原理在一起就好了。为什么是直径的一半呢?因为两个一半就可以拼成一个完整的直径。
偶数情况(如图一):
- 两个蓝色的节点都是中心,他们之间有一条连边,所有的直径都会经过这条边。所以说,我们只需要统计左边(也就是中心 \(1\) 的子树)和右边(中心 \(2\) 的子树)。这两边里面的直径一半的个数直接相乘那就是答案,原理与奇数情况是类似的。
我们先要处理出中心,然后从中心再往外 DFS 即可。
link。
G
这是我第一道正经的黑题,鼓掌!
这道题精妙在于将整个图旋转 \(45\) 度,虽然可能要画图,但我感觉不用画图也是可以理解的了。
为什么要旋转 \(45\) 度呢?
我们先把所有种类的操作的偏移量列出来。
-
\(L(-d_i,0)\)
-
\(R(d_i,0)\)
-
\(U(0,d_i\)
-
\(D(0,-d_i)\)
发现有三种可能的值,有点难搞,怎么办?如果将图旋转了一下,会发生什么呢?
-
\(L(-d_i,-d_i)\)
-
\(R(d_i,d_i)\)
-
\(U(-d_i,d_i)\)
-
\(D(d_i,-d_i)\)
这样,只有了 \(d_i\) 和 \(-d_i\)。
依然不太好搞。然后,我们可以将最终答案的横纵坐标减去 \(\sum_{i=1}^n d_i\)。这样,每一次的操作就变成了:
也就是说,每一次的操作横纵坐标都加上 \(d_i\)。
-
\(L(0,0)\)
-
\(R(2\times d_i,2\times d_i)\)
-
\(U(0,2 \times d_i)\)
-
\(D(2\times d_i,0)\)
这样,我们发现了横纵坐标是不会互相依赖的,都是独立的,我们可以对他们进行单独计算,最后拼起来即可。
如何计算能否拼成功呢?那么我们就用到可行性背包问题。
到最后,我们从后往前记录路径就可以了。
link。
H
第一次做 H 题,鼓掌!
对于这种计数类的,一般都是 Dp。
我们设 \(dp_{i,j}\) 代表已经选了 \(i\) 个数,总和 \(j\) 的时候的方案数。
由于正着做比较麻烦,所以考虑另一种方向。
-
添加一个数 \(0\)。\(dp_{i,j}\) 加上 \(dp_{i-1,j}\)。
-
将所有的数加上 \(1\)。\(dp_{i,j}\) 加上 \(dp_{i,j-i}\)。
我们考虑如何处理最多 \(m\) 个同样的数的要求,那么我们要限制最多连续添加 \(m\) 个 \(0\)。
我们如何控制呢?所以我们再开一个数组 \(g_{i,j}\),转移方式只有将所有的数加上 \(1\) 的操作。
因此我们可以得到转移方程:
\(dp_{i,j} = dp_{i,j-i} + \sum_{x=1}^m g_{i-x,j}\) 和 \(g_{i,j} = dp_{i,j-i}\)。
时间复杂度依然不太行,主要原因在于 $ \sum_{x=1}^m g_{i-x,j}$。
如何解决?我们发现可以直接搞一个前缀和优化,前缀和数组维护着 \(g\) 数组。
所以,时间复杂度为 \(O(n^2)\)。
link。
*2024 3 28 ABC223 VP(OI赛制)
A
B
C
直接二分即可,注意精度。
link。
D
直接 topo 即可,用优先队列存储每一个点,注意递增顺序,而且注意判断无解的方式。
[link[(https://atcoder.jp/contests/abc223/submissions/51710440)。
E
我们发现其实最终情况只有两种可能:
-
三个横的拼在一起。
-
两个横的一个竖的。
当然,三个竖着的也是可以的,我们可以将三个横的旋转一下即可,第二种情况同理。不考虑旋转的情况下只有这两种。于是,我们可以对其分类讨论。
实现并不难,主要在于细节。
我们可以设置一个函数 \(get(x,y)\) 它代表的是面积为 \(x\),一条边为 \(y\),另一边最小的就是 \(get(x,y)\)。
注意,有些数要判断其 \(>0\)。
link。
F
这里我们引入一个科技:AtCoder library。他就是一个 AtCoder 自己的库,里面有很多封装好的函数。可以直接用,我们可以在:link 了解详情。
假设,你已经会了 AtCoder 库的线段树用法,那么就可以开始讲了。
首先,我们思考一下一个合法的括号匹配的标准是什么?
在这个括号序列里,假设我们左括号设为 \(1\),右括号为 \(-1\)。
满足的条件:
-
这个括号序列对应的数字任意一个前缀的前缀和都大于等于 \(0\)。
-
结尾的括号序列前缀和为 \(0\)。
所以说,我们线段树要维护两个值,一个是前缀和下的最小值,另一个是前缀和。
所以我们每一次修改,只需要交换一下,改变一下这个点的值,然后就用线段树来维护,查询的时候直接判断上面条件是否满足即可。
让你见识科技的力量,线段树题目实际代码 \(20\) 行,爽!
link。
G
首先引入一个定理:
树的最大匹配数量为点数量减去二分图最大权独立集。
考虑树型 DP。
我们设 \(fa_i\) 代表的是 \(i\) 的父节点。
设 \(f_{i,j}\)。\(j\) 为 \(0\) 或 \(1\),表示的是 \(i\) 这个点的子树,是否选择(\(j\) 的布尔值表示)的最大权独立集。
\(g_{i,j}\),为选不选(\(j\) 的布尔)\(fa_i\) 这个点的时候除了 \(i\) 这个子树内,其他所有点的最大权独立集。
所以我们可以推出 DP 转移方程,此处 \(v\) 代表 \(u\) 的连边。
\(f_{u,0} = \sum_v \max(f_{v,0},f_{v,1)}\)。\(f_{v,1} = \sum_v f_{v,0} + 1\)。
\(g_{u,0} = \max(g_{fa_u,0},g_{fa_u,1}) + f_{fa_u,0} - \max(f_{u,0},f_{u,1})\)。
最后记录数量即可。
link。
*2024.3.31 ABC211 VP (OI赛制)
C
很水直接递推就好了。
link。
D
这是一个很经典的问题,就是最短路计数。正常的最短路 dij 我们是开一个 \(dis_x\) 代表到达 \(x\) 的最短步数,那么怎么做到计数呢?我们只需要给 \(dis\) 开成一个 pair,另一个数记录这个出现了多少次即可,只用在模板单源最短路上添加对次数的记录即可通过本题。link。
E
这道题也很简单,由于数据范围非常小,所以我们只需要考虑最暴力的方式直接搜索。我们直接枚举每一个起点,然后对他进行 DFS,最多走 \(k\) 步,所以时间复杂度就是 \(n^2 \times 4^k\),数据非常充裕,所以可以通过本题。
link。
F
这一看,哎呀,不是扫描线板子吗!!
显然就是,但是我们不用写臭长的线段树,只需要写树状数组即可。
难点在于这一道题它的每一个形状都不一定是一个四边形,所以比较麻烦,我们需要对这个图形的每一个顶点打标记(差分)即可。
我们可以找到最接近 \(y\) 轴的那个点开始,然后逐渐往后遍历每一个点,这必定是一个是 \(1\) 一个是 \(-1\) 这样间隔排序的,所以开一个 \(tmp\) 记录他是 \(1\) 还是 \(-1\)。
我们可以记录下每一个 \(x\) 坐标下 \(y\) 有多少个点,将它放到一个 vector 里。我们将问题离线下来,对于每一个 \(x\) 都对应一起处理,对于他们的 \(y\) 直接用树状数组维护即可,如果你想用 Seg 也可以。
最后我们再把答案依次输出即可。
link。
G(CF505D)
紫题。
首先我们发现先答案最多为 \(n-1\)。如果答案是 \(n-1\) 那么图是一个树,因此可以连通。
我们可以先将 \(ans = n - 1\),然后对答案做减法,我们将每对 \((u,v)\) 需要在一个集合内的用并查集维护起来。然后记录一下,知道有 \(x\) 个不同的并查集,然后用 \(ans\) 减去 \(x-1\),也就是每一个集合之间最少的通道,他们通道减去就完事了。
我们也可以将一开始 \(ans=n\),然后处理完之后 \(ans\) 减去 \(x\) 即可,会方便一些。
然后呢,如果对于一个连通块内有环,那么必定不是一棵树了,它的边数就不再是点数 \(-1\) 了,而是点数,所以说,如果是环的情况,我们要再让 \(ans\) 加一。
判环可以使用 topo。
link。
*2024.4.17 ABC208 VP(OI赛制)
D
先看数据范围,哦?\(n \le 400\),这显然给 \(O(n^3)\) 开的友好数据范围!!!
由于是最短路,想到 Floyd,如果你只知道他的转移公式是 \(dis_{i,j} = dis_{i,k} + dis_{k,j}\) 的话,并且只会在最短路题里偷懒,那你真的没有学 Floyd。我们想想他的本质是啥?
显然,那个 \(k\) 是新加入进来的节点,然后所有 \(i\) 和 \(j\) 都会经过 \(k\) 做一条线段,更新他们的最短路。
那么,你可以做这一题了,所以你会发现,哎呀,这题求得不就是我们每一个转移方程的累加和吗?对的没错!!
所以在跑 Floyd 的时候记录 \(sum\) 即可。
link。
E
这显然是一个数位 DP,那么我们可以用记忆化搜索来实现,由于方便一些,就这样搞。
我们记录状态也就可以用 map 了。
int dfs(int p,int fg,int front0,int cnt)
这是我的 DFS 的参数。
\(p\) 位,\(fg\) 是否受进位限制,\(front0\) 前导 \(0\),\(cnt\) 目前答案。
我们把需要知道的参数都给列出来了,这样我们就可以直接递归转移,每一次枚举能选哪些数,然后开一个 map 对其状态记录。
这样,就做完了。
link。
*2024.4.17 ABC212 VP(OI赛制)
D
第一时间想到数据结构,但是发现,这个数加了,只会影响前面的数,于是五分钟秒了。
我们记录一个 \(tot\) 代表这个操作以及以前的加的数总和。
加入 \(x\),我们在 set 里加入 \(x-tot\),这样,对于以后任何一个时刻的 \(tot\)(例如 \(tot_2\)),那么再用 \(x-tot\) 加上 \(tot_2\),这样就可以保证只有后面的加法会影响到他。
然后每一次删除直接把 set 的最小数踢走即可。记得,此时这个数还要再加上此时的 \(tot\)。
link。
E
这一道题我们用的是容斥原理。
考虑最暴力的 Dp,\(dp_{i,j}\) 为从 \(j\) 的时间走到 \(i\) 点的方案数,\(dp_{i,j} = \sum_{k} dp_{k,j-1} [k 可到达 i] + dp_{i,j-1}\)。
考虑容斥,变成 \(dp_{i,j} = \sum_{k=1}^n dp_{k,j-1} - dp_{i,j-1} - \sum_{k} dp_{k,j-1} [k 不可到达 i]\)。
我们发现 \(\sum_{k=1}^n dp_{k,j-1}\) 对于同一个 \(j\) 来说都是一样的,我们可以对每一个 \(j\) 一开始将他先算出来,记录成 \(sum\),于是,转移方程变成了:\(dp_{i,j} = sum - dp_{i,j-1} - \sum_{k} dp_{k,j-1} [k 不可到达 i]\)。
又因为 \(\sum_{k} dp_{k,j-1} [k 不可到达 i]\) 是非常少的,因为总共也就是有 \(M\) 条边。
因此我们使用 \(sum = \sum_{k=1}^n dp_{k,j-1}\),\(dp_{i,j} = sum - dp_{i,j-1} - \sum_{k} dp_{k,j-1} [k 不可到达 i]\) 的转移方程时间复杂度正确,即可通过本题。
link。
F
这道题有一个很显然的结论:
- 在坐完每一辆车之后必定会座离你最近到达的车,因此在每一辆车之后有唯一对应的一辆车作为后继,考虑建图,这就是一条树边。你会发现,这,其实就是一棵树。
然后对于每一个点有 $ T - S$ 的时间代价,他们两辆车之间也有,所以只需要处理出每一条树边的边权,那么你要找一个时刻,相当于在树上进行倍增。
倍增也不是很难。这题就是细节非常的多。
具体看代码,代码比较短。
link。
*2024.4.17 ABC229 VP(OI赛制)
E
又是一个 Water 题。五分钟秒了。
显然,正难则反,题目要求删除,我们倒着来,变成加边。这样它的操作就是不断加边,然后顺序给你了,问你每一个时刻的连通块的数量。
是一个并查集模板,如果两个点合并了,那么就会少了一个连通块,更新 \(ans\) 即可。
我们可以把所有答案堆进一个栈里面。
然后到最后再把它倒出来输出即可。
也没有什么注意的,纯板子。
link。
F
诈骗!!!
我们直接考虑 Dp。
由于二分图判定法有一个叫做黑白染色法。
通过染色 \(0\) 和 \(1\) 来判定二分图。
所以我们在转移的时候也一定要考虑到这个点。
设 \(dp_{i,j,k}\) 为已经染色了前 \(i\) 个点,然后此时 \(i\) 的颜色为 \(j\),\(1\) 的颜色为 \(k\)。
所以我们就可以得出转移方程:
- \(dp_{i,0,0} = \min(dp_{i-1,0,0}+b_{i-1},dp_{i-1,1,0}) + a_i\)
- \(dp_{i,0,1} = \min(dp_{i-1,0,1}+b_{i-1},dp_{i-1,1,1}) + a_i\)
- \(dp_{i,1,0} = \min(dp_{i-1,1,0}+b_{i-1},dp_{i-1,0,0})\)
- \(dp_{i,1,1} = \min(dp_{i-1,1,1}+b_{i-1},dp_{i-1,0,1})\)
很好理解,我们要保证根中间的节点保持不一样的颜色,和上一个节点也保持这不一样的颜色。
分四种情况讨论就是这样。
link。
G
非常好的一道题。
思维要求蛮高的。
我们可以将体面转换一下,例如一个 Y 他要从 \(x\) 走到 \(y\),那么他所需要的步数就是 \(x\) 到 \(y\) 之间 . 的个数。
那么我们对于一个区间 \([l,r]\),就变成了,这上面每一个点有一个数,找一个点然后是的所有的点到他的距离最小,这是一个很经典的问题,这个时候的策略就是选中间点。
我们可以直接二分长度,然后枚举每一个区间,然后计算一下是否符合条件。
我们可以通过一个前缀和和一个二次前缀和搭配使用来算出他所需要的次数。
在 check 函数里即可达到线性的时间复杂度。
link。
*2024.4.17 ABC191 VP(OI赛制)
D
恭喜你水了一道蓝题。
首先,由于是整点,我们不妨枚举一个维度。
我这里枚举 Y 坐标。
但是此时要计算有多少个不同 X 坐标点。
如图:
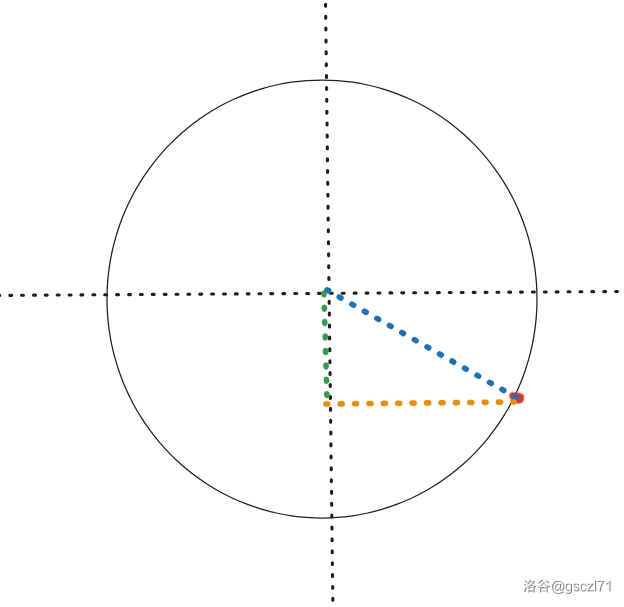
由于我们枚举,知道绿线长度,然后蓝线即为半径,那么可以用小学一年级学的勾股定理来求出橙色线的距离,然后我们将他向下取整就是这右边的点数。
这样通过枚举,就做完了。
但是由于他很恶心,卡你精度,所以你要把 \(r\) 加上一个很小很小的偏移量,因为有些恰好压着原边的点会被卡掉。
link。
E
这也比较水。
时间复杂度宽松,允许 \(O(n \times m \log n)\)。也就是 \(n\) 遍 dij。堆优化显尽了稀疏图强大优势。
那,我们 dij 最短路如何求一个环呢,很简单,\(dis_{x,y}\) 代表 \(x\) 到 \(y\) 的最短路径,那么,如果 \(y\) 连向 \(x\) 有一条权值 \(z\) 的边,那么他们这个环的长度就是 \(dis_{x,y} + z\)。
我们直接枚举每一个出发点,然后跑最短路,再根据上述方法算出最小值。
那么就可以得出答案了。
link。
F
首先先发现一个性质,如果我们要用 GCD,那么这个数必然要比其他数小,不然,它会被 min 操作淘汰。
我们可以用一个 \(mp\) 来记录这个数和一些 \(a_i\) GCD 起来的结果。当一个 \(a_i\) 是这个数的倍数的时候他会一起 GCD。
如果经过多次 GCD 之后 \(mp_i = i\)。那么代表作为他倍数的所有 \(a_j\) 他们的最大公因数就是 \(mp_i\)。
如果遇到这种情况直接加上一个贡献。
注意,在 gcd 的时候还要判断一下这个数一定比最小值小才可行。方便起见,直接先对 \(a\) 数组排序。
link。
*2024.4.17 ABC240 VP(OI赛制)
F
这个要做两个前缀和。
\(C\) 题目已经给出,那么我们可以跟据他来求 \(B\)。
首先,我们可以把 \(C\) 看成 \(n\) 个组,每一组要不是正数要不是负数,所以导致 \(B\) 在一段区间内不断增加或者不断减少,而且每一段连续增加或者连续减少的段数也只有 \(n\)。
然而 \(A\) 却又因为 \(B\) 的数值来进行增加或减少。
再来看 \(B\),它的每一段同符号的区间数量只有 \(2\times n\)。(同符号只都是正或者都是负)举个例子,最极端的情况,此时负数,然后有一个正数的 \(C\) 把他加到了正数(变了符号),那么产生了两个不同的区间。正变负也是同理。
然而,我们又可以计算每一段 \(C\) 的区间对应的 \(B\) 是什么时候变号的(除一下就知道了)。那么我们就可以知道 \(B\) 中那些段是全是正数或者全是负数。
然后小学一年级的等差数列求和,我们就可以计算出这个 \(B\) 这一段区间结束后的贡献。
然后每一次更新答案。
注意,一开始,\(ans\) 要设成 \(C\) 中的第一个数,因为,如果这都是负数,会把你卡掉,这样其实实际上第一个数最大,而你却算成了第一个数所在区间的最后一个数。
因此这道题做完了。
link。
G
这道题很像这一道题。
我在这题写了题解,比较详细,这里。
难度黑题,关键就是一个点非常巧妙,非常难想到。将整一个图旋转一下,这样就可以独立两个维度,因此,再加上一些处理,可以背包。
但这道题稍有点不同。
这道题变成了立体空间,三维!那我们该如何处理呢?
我们可以直接枚举其中一个维度,变成二维上走到 \((y,z)\) 的方案了。
根据那个黑题的思想,我们可以将图旋转,相当于走到 \((y-z,y+z)\)。两个维度也独立,可以分别操作。
我们再引出一个式子。
如果 \(a\) 次 \(-1\),\(b\) 次 \(+1\)。
当你走了 \(s\) 步,最终想要走到 \(t\)。
那么可以的出这两个式子:
\(a-b=t\) 和 \(a+b=s\)。
因此我们可以算出 \(a=\dfrac{s+t}{2}\),\(b=\dfrac{s-t}{2}\)。
那么我们把他应用到这道题上面,这一道题的要求就是最终要到达 \((y-z,y+z)\),设他要走 \(k\) 步。
所以它的方案数可以用组合数学来表示,用到的是乘法原理。
\(C_k^{\dfrac{k+y-z}{2}} \times C_k^{\dfrac{k+y+z}{2}}\)
我们还需要判断一下如果不是 \(2\) 的因数的话,那么是不合法的。
因此,最后的方案数就直接乘法原理即可。
某位小朋友只会用 lucas 求组合数,被 T 飞了,于是用了逆元预处理。
link。
本文来自博客园,作者:gsczl71,转载请注明原文链接:https://www.cnblogs.com/gsczl71/p/17880643.html
gsczl71 AK IOI!RP = INF 2024年拿下七级勾!

 浙公网安备 33010602011771号
浙公网安备 33010602011771号