图论算法
链式前向星
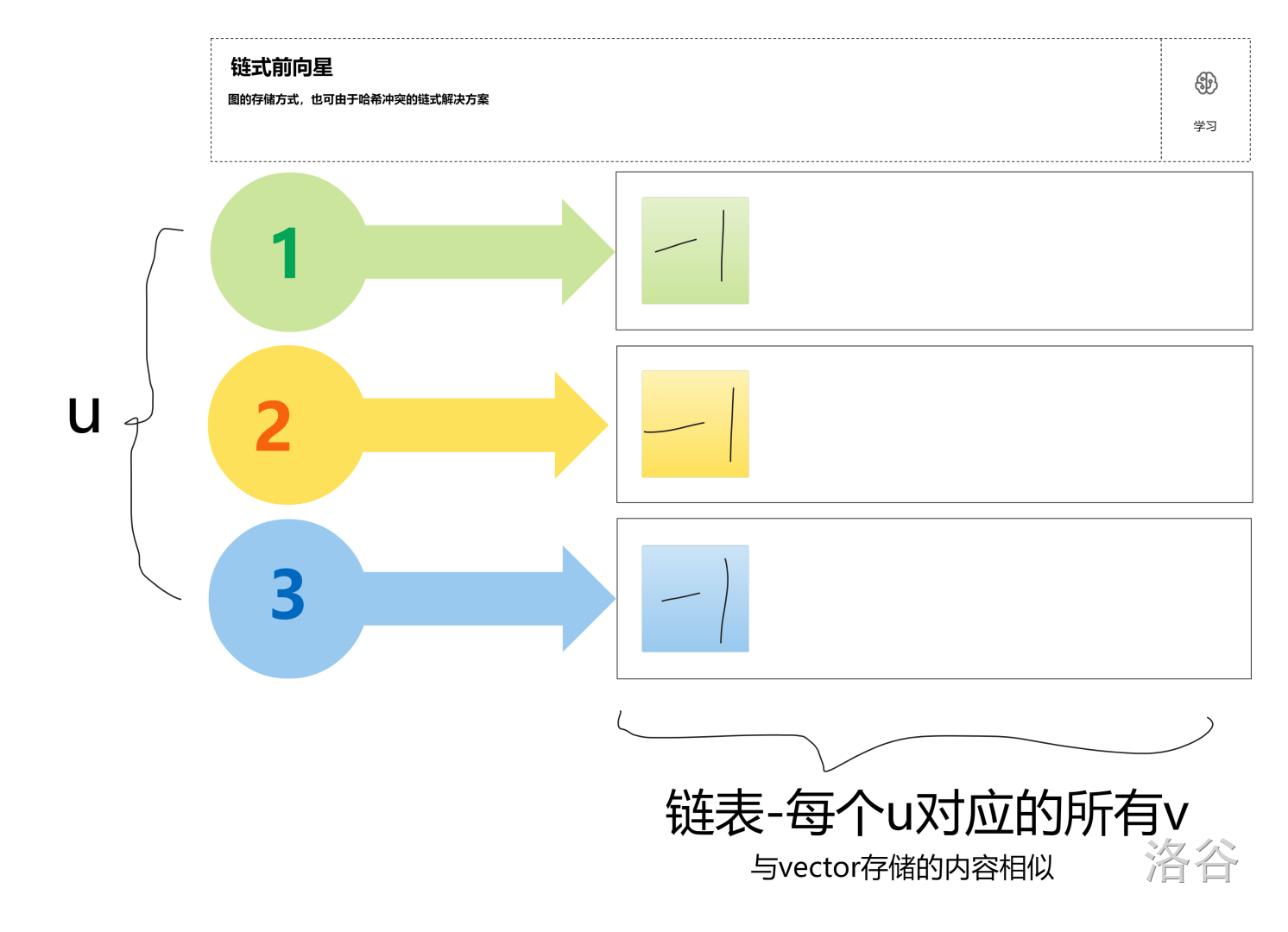
首先先初始化一个数组: \(head[N]\) 代表每一个 \(u\) 指向第一个 $ v$。
初始化时需要将其初始化为 \(-1\),表示每个 \(u\) 没有连的边
初始化
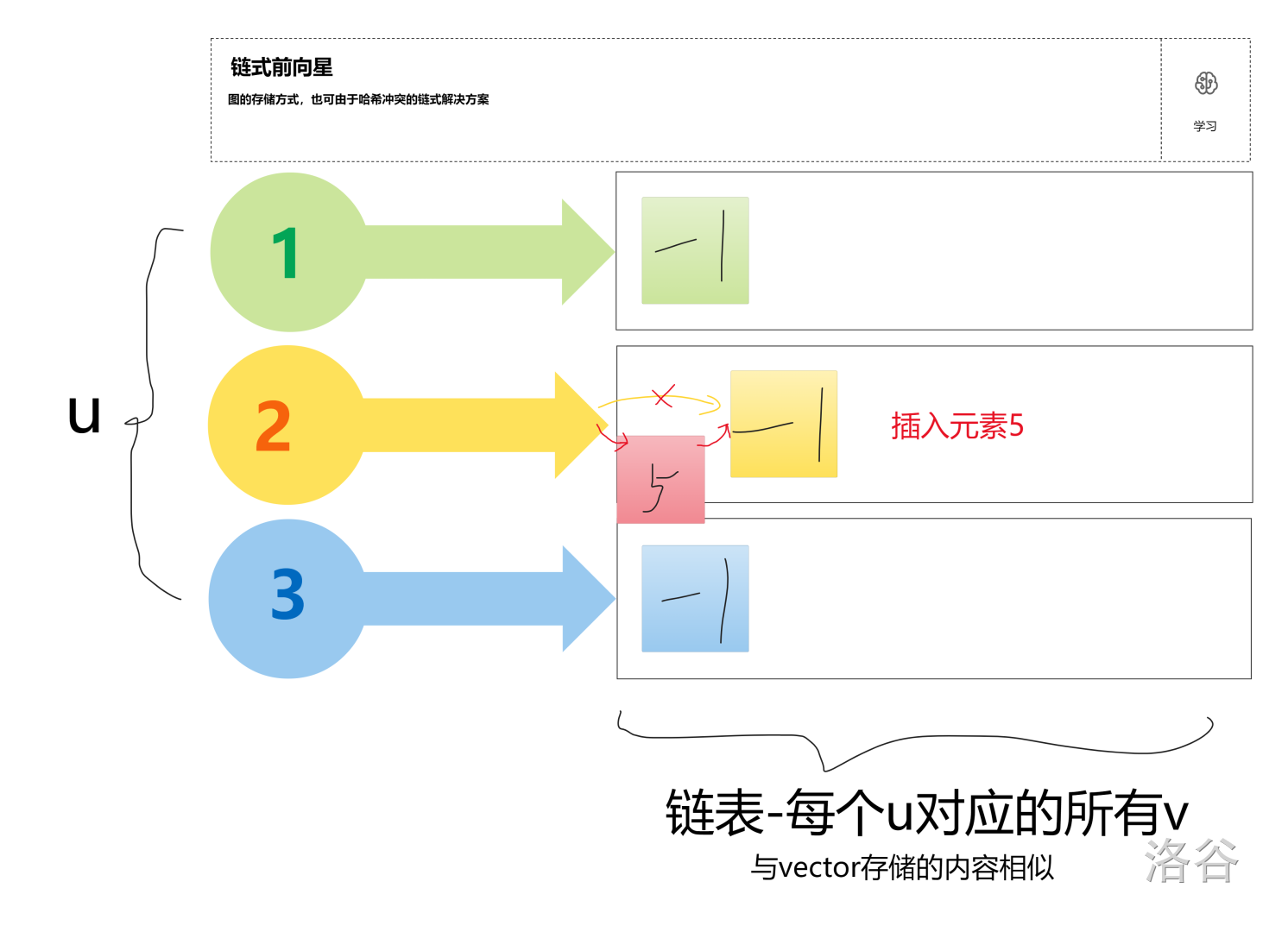
链式前向星使用的是插头法:每一个元素与插入链表中都是再最前面的。
插入
例如:输入一条 \(2 - 5\) 的边,此时调用函数 \(add(2,5)\),那么在 \(2\) 这个链表的首元素插入 \(5\)。如图:
- 第一步,先给 \(5\) 设置一个 $ id$( \(id\) 是每插入一个元素都++的)
- 第二步,将 \(5\) 的 \(nxt\) 数组等于 $ head[2]$ ,\(head[2]\) 代表的就是原本 \(-1\) 的 \(id\),那么将 \(5\) 的下一个元素设为这个 \(-1\) 的 \(id\),其实 \(nxt\) 数组可以理解伪指针。
- 第三步,把 \(head[2]\) 的指向变成 \(5\),改变指针
- 第四步,用一个数组记录每一个 \(id\) 的值,即 $ 5$ 的 \(id == 1\),那么 \(vel[1] = 5\)
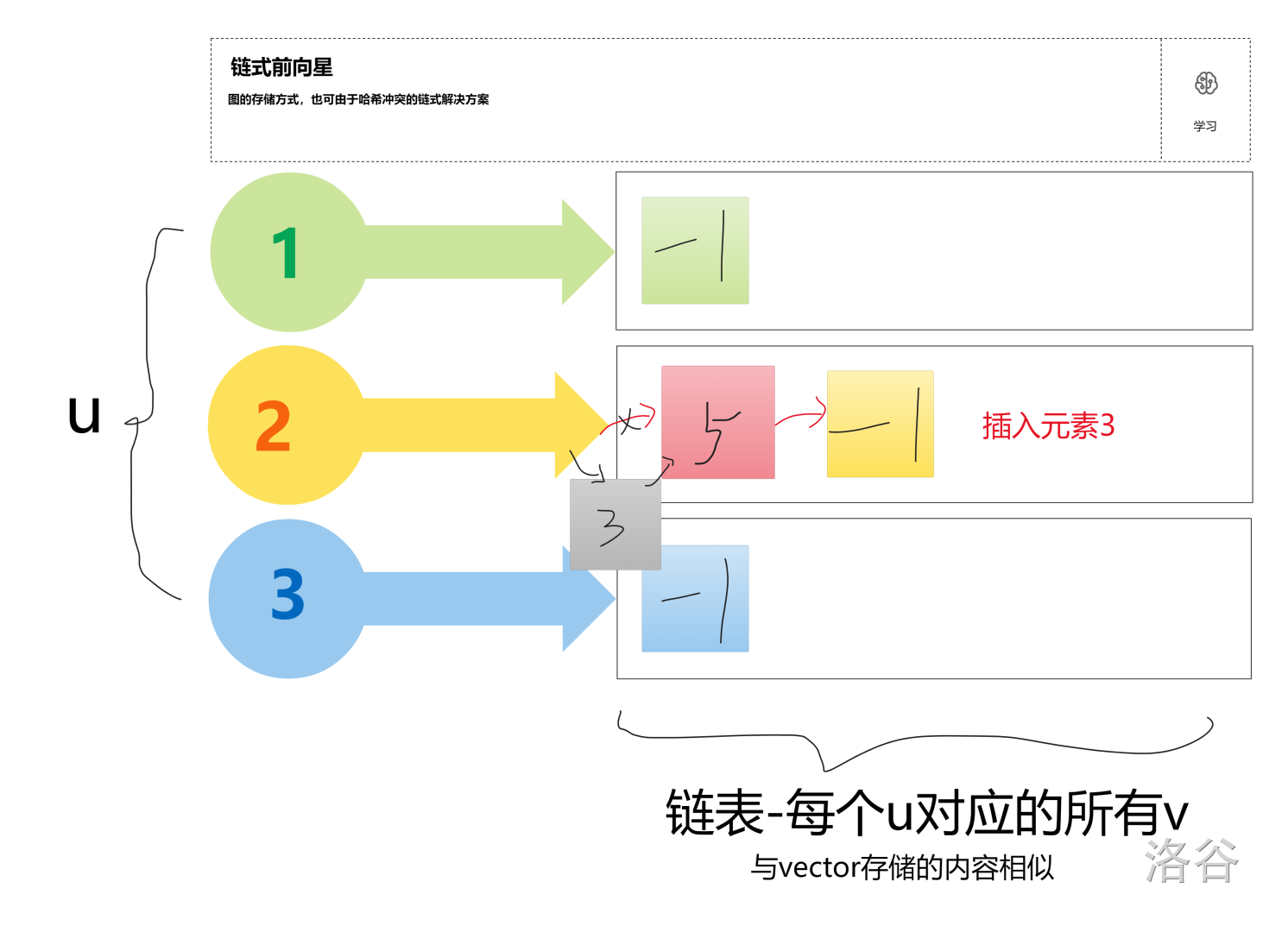
类似的,再插入一个元素也一样
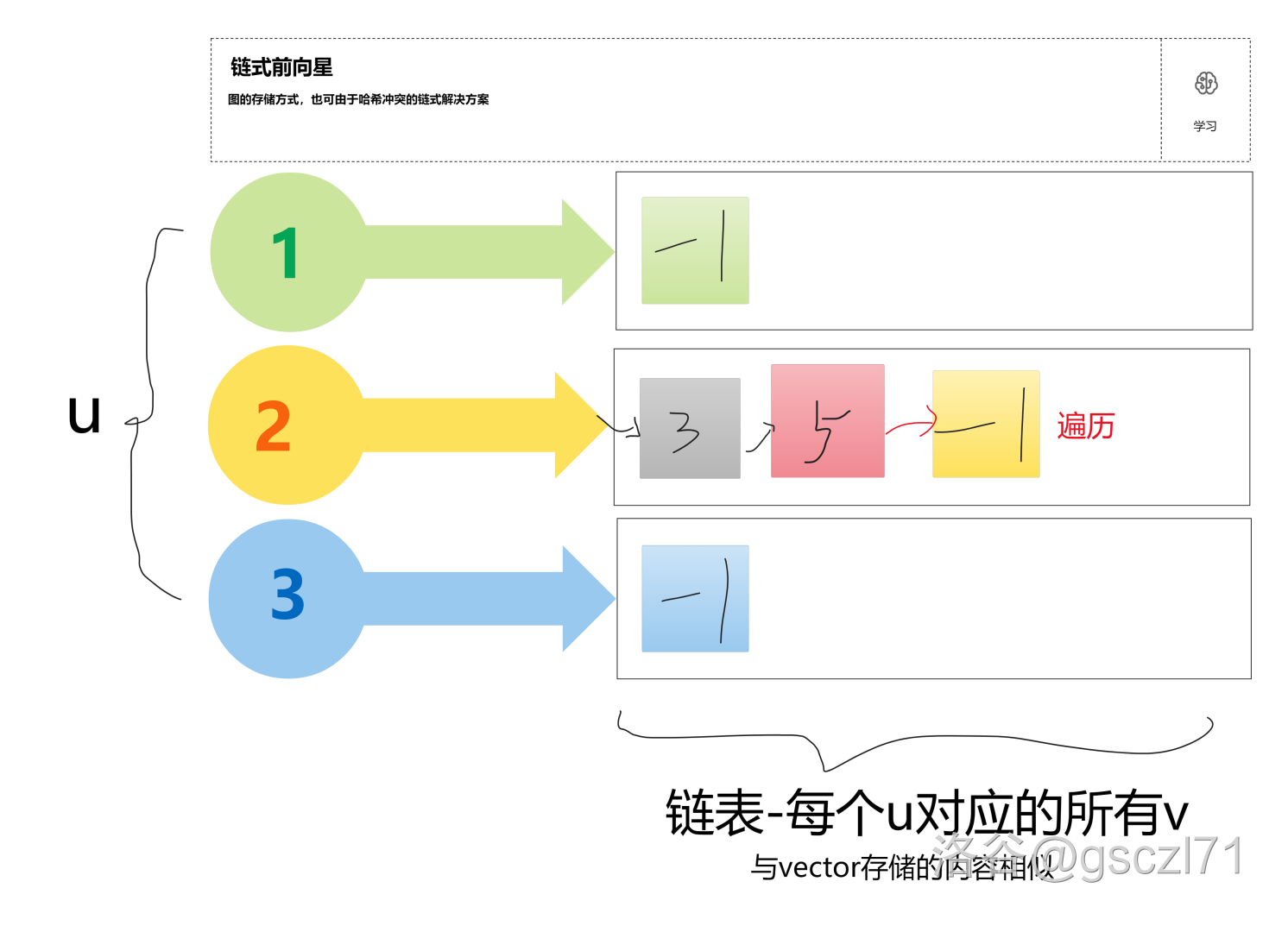
遍历
- 将$ i $指向要遍历的 \(u\)(此处为 \(2\))的 \(head\)
- 每次 \(for\) 循环 \(i=nxt[i]\),即指向下一个指针。
- 如果 \(i==-1\) 那么代表已经走到尽头了,所以就作为终止条件
链式前向星一定要记得初始化!
// head[u] 和 cnt 的初始值都为 -1
void add(int u, int v) {
nxt[++cnt] = head[u]; // 当前边的后继
head[u] = cnt; // 起点 u 的第一条边
to[cnt] = v; // 当前边的终点
}
// 遍历 u 的出边
for (int i = head[u]; ~i; i = nxt[i]) { // ~i 表示 i != -1
int v = to[i];
}
copy一份oiwiki模板
强连通分量
Tarjan
抽象难懂的算法
第一次接触链式前向星,本算法储存方式为链式前向星,用vector不香吗
这个算法很多什么low啊,dfn啊,把你搞得很晕……
其实整个算法就是基于DFS然后再加上玄学打标记搞定的。
这里只介绍Tarjan求割点 (因为其他我不会。
前置知识
链式前向星
见前面
割点
通俗的讲,就是一个图只要把这个点割了,就不连通了。
时间戳
在进行DFS的时候对每个点编号的方式,就是dfs第几个遍历到的。
搜索树
用DFS在一个 \(n\) 的图中构建一个 \(n-1\) 的数,感觉跟生成树比较像,但是是用DFS构造的
追溯值:low
low值得定义
书面定义:
设以x为根的搜索树子树为subtree(x),low(x)为x以下结点的dfn的最小值
- sub(x)中的结点
- 通过一条不是搜索树中的边到达一个sub(x)的点
很晕对吧,我也不懂(copy别人的。
于是我就用我理解的语言来讲解
这里就盗用OI wiki中的图片来讲解
我认为这个就是tarjan中令人难懂的一个点。
假设,我们已经对dfn进行了初始化。每个点上的值就是其dfn的值。图中黑色的边就是树边,也就是一个dfs生成树中的边。
而有一条红色的边,他不是树边,它却指向了一个dfn值比他小的边,也就是直接指向了自己某个祖宗。所以这个边就叫做返祖边。
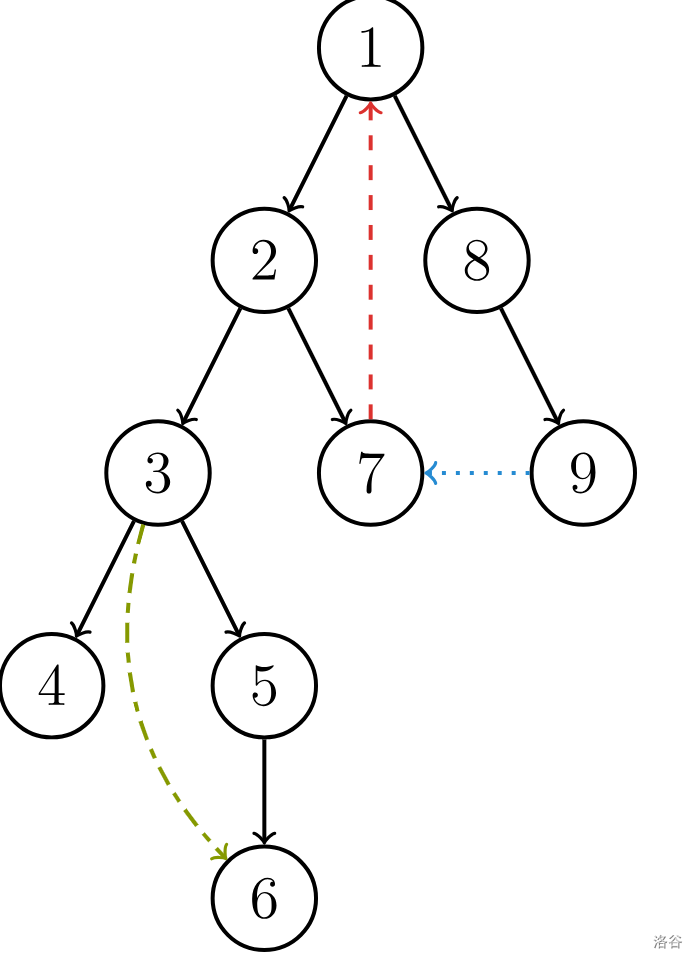
如果此时还有一条返祖边(7,8)。(如图所示):
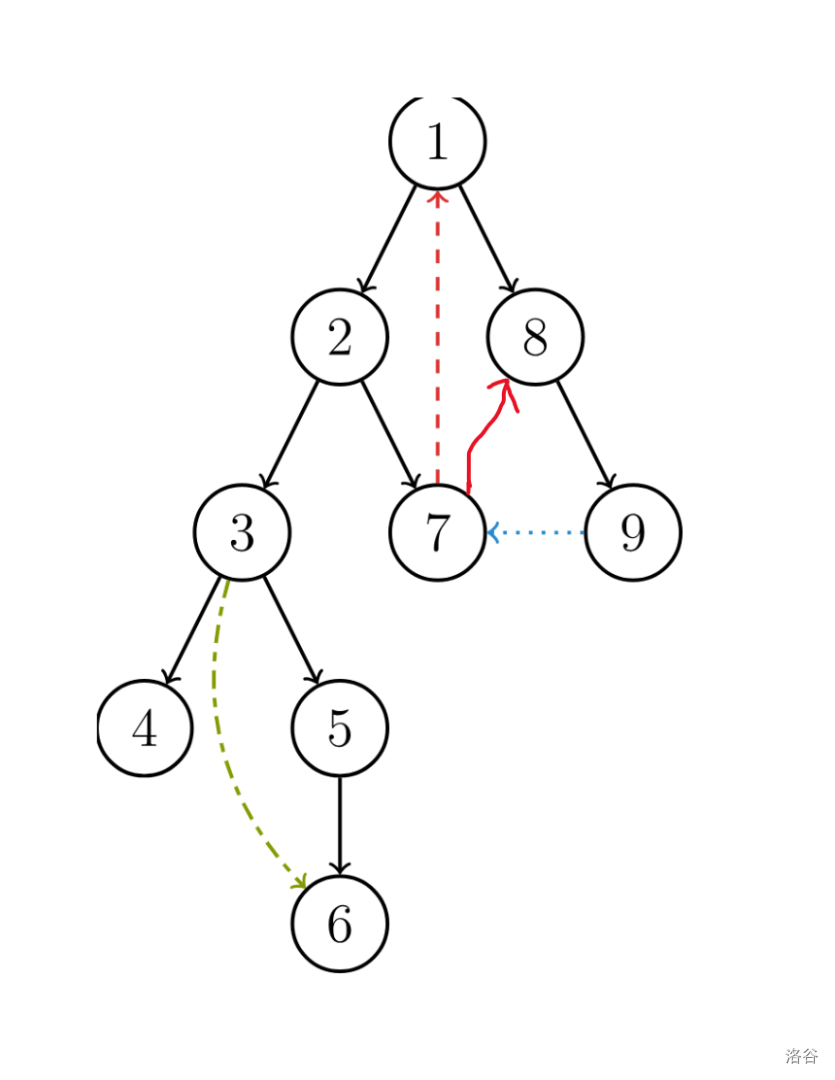
结论:那么对于结点7他的low值就是1。
为什么呢?
因为有(7,1)和(7,8)这两条返祖边使得结点7连向了结点1和结点8,因为 \(1<8\) 所以 \(low_7\) 为 \(1\)。
接下来,我们考虑如何计算low值
初始化:很容易想到 \(low_i\) = \(dfn_i\)。因为连到自己也是可以的嘛。
如果对于 \(x\),有一个 (\(x\),\(y\))的连边。
-
如果y是在搜索树中x的子树内,那么 \(low_x\) = \(min(low_x,low_y)\)。因为如果它的子树有一条连到更小的点的返祖边,那么肯定也得算上它自己
-
如果(\(x,y\))不是一条树边(就例如7和9吧)。那么只能用 \(dfn_y\) 来更新 \(low_x\) ,因为他们又不是一个搜索树中,所以最多就只能说是 \(x\) 有连了一条边到了 \(y\) 。那么最多也就是更新一下到达的点中最小的值而已(就是low)。再根据定义,它不满足上一条条件吗,所以无法继承y的low值。
计算割点
Tarjan算法告诉我们,如果 \(y\) 是 \(x\) 的子节点且 \(low_y > dfn_x\)。那么 \(x\) 就是割点。
为什么呢?因为根据树的定义,\(y\) 有且仅有一条边连向它的祖先(包括他父节点\(x\))。那如果 \(y\) 除了这条连向祖先的边,只能访问到比\(x\)后遍历到的结点(也就是 \(dfn\) 比 \(dfn_x\) 还大 的结点)。也就意味着如果把 \((x,y)\) 这条边给断掉了,\(y\)无法访问到比\(x\)的dfn小的结点。那么就不连通了,所以此时 \(x\) 就是割点。
但是:这个对于根节点肯定是行不通的!!
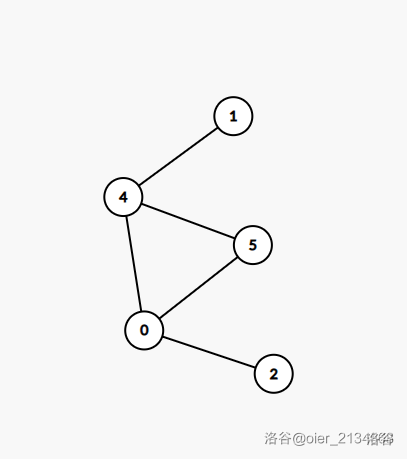
就像上面的那个图,
如果根节点用以上方法判定,那就会判定成割点,但是显然不是。所以引出了新的判断根节点的方式:如果搜索树的根节点有两棵即以上的子树,那么根节点为割点。显然,如果把根节点割去,那么两个子树不互相连通,即为割点。
OI-wiki P3388 代码
/*
洛谷 P3388 【模板】割点(割顶)
*/
#include <bits/stdc++.h>
using namespace std;
int n, m; // n:点数 m:边数
int dfn[100001], low[100001], inde, res;
// dfn:记录每个点的时间戳
// low:能不经过父亲到达最小的编号,inde:时间戳,res:答案数量
bool vis[100001], flag[100001]; // flag: 答案 vis:标记是否重复
vector<int> edge[100001]; // 存图用的
void Tarjan(int u, int father) { // u 当前点的编号,father 自己爸爸的编号
vis[u] = true; // 标记
low[u] = dfn[u] = ++inde; // 打上时间戳
int child = 0; // 每一个点儿子数量
for (auto v : edge[u]) { // 访问这个点的所有邻居 (C++11)
if (!vis[v]) {
child++; // 多了一个儿子
Tarjan(v, u); // 继续
low[u] = min(low[u], low[v]); // 更新能到的最小节点编号
if (father != u && low[v] >= dfn[u] &&
!flag
[u]) // 主要代码
// 如果不是自己,且不通过父亲返回的最小点符合割点的要求,并且没有被标记过
// 要求即为:删了父亲连不上去了,即为最多连到父亲
{
flag[u] = true;
res++; // 记录答案
}
} else if (v != father)
low[u] =
min(low[u], dfn[v]); // 如果这个点不是自己,更新能到的最小节点编号
}
if (father == u && child >= 2 &&
!flag[u]) { // 主要代码,自己的话需要 2 个儿子才可以
flag[u] = true;
res++; // 记录答案
}
}
int main() {
cin >> n >> m; // 读入数据
for (int i = 1; i <= m; i++) { // 注意点是从 1 开始的
int x, y;
cin >> x >> y;
edge[x].push_back(y);
edge[y].push_back(x);
} // 使用 vector 存图
for (int i = 1; i <= n; i++) // 因为 Tarjan 图不一定连通
if (!vis[i]) {
inde = 0; // 时间戳初始为 0
Tarjan(i, i); // 从第 i 个点开始,父亲为自己
}
cout << res << endl;
for (int i = 1; i <= n; i++)
if (flag[i]) cout << i << " "; // 输出结果
return 0;
}
最小生成树
kruskal
前置知识:并查集
按照边的权值递增去取,如果形成一个环,那么就不选。
环是用并查集来维护。
#include<bits/stdc++.h>
using namespace std;
const int N = 5005,M = 2E5 + 1;
struct node{
int u,v,w;
}a[M];
bool cmp(node a,node b){
return a.w < b.w;
}
int s[N];
int find(int x){
//并查集
if(s[x]!=x){
s[x] = find(s[x]);//路径压缩
}
return s[x];
}
int n,m;
void kruskal(){
sort(a+1,a+m+1,cmp);
for(int i=1;i<=n;i++) s[i]=i;//并查集初始化,每一个元素都是独立的集合
int ans=0,cnt=0;
for(int i = 1;i <= m;i++){
//逐步遍历每一条边
if(cnt == n-1) break;//优化,在已经足够的边之下可以退出
int e1 = find(a[i].u);
int e2 = find(a[i].v);;
if(e1==e2)continue;//在一个集合内,有公共祖先,代表有环退出
else{
ans += a[i].w;
s[e1]=e2;//并入一个集合
cnt++;//已增加一条边
}
}
if(cnt == n-1)cout<<ans;
else cout<<"orz";
return ;
}
int main(){
cin >> n >> m;
for(int i = 1;i <= m;i++) {
scanf("%d%d%d",&a[i].u,&a[i].v,&a[i].w);
}
kruskal();
return 0;
}
prim
和dij思想差不多(同一个人发明的
选择任意节点出发,每一次加入没有走过的点的最小权值。
//prim 普利姆算法
#include <bits/stdc++.h>
using namespace std;
const int N = 5005,M = 2e5+5;
struct node{
int to,w;
};
int n,m;
bool done[N];//是否加入了生成树中
vector <node> g[M];
struct data{
int id,dis;//点,边
bool operator < (const data & u)const {return dis > u.dis;}
};
void prim(){
int s=1;//从任一点开始
for(int i = 1;i <= n;i++) done[i]=false;//初始化
priority_queue<data> q;
q.push({s,0});
int ans=0,cnt=0;
while(!q.empty()){
data f = q.top();
q.pop();
if(done[f.id]) continue;//这个点已经在生成树中了,跳过
done[f.id]=1;
ans+=f.dis;
cnt++;
for(auto it:g[f.id]){
//遍历下面的点
if(done[it.to])continue;
q.push({it.to,it.w});
}
}
if(cnt==n)cout << ans;
else cout <<"orz";
}
int main(){
cin >> n >> m;
for(int i = 1;i <= m;i++){
int u,v,w;
cin >> u >> v >> w;
g[u].push_back({v,w});
g[v].push_back({u,w});
}
prim();
return 0;
}
两种算法在不同的图中有不同的优势
kruskal: \(O(m\log m)\)
prim: \(O((n+m)\log n)\)(二叉堆优化,像dij一样)
最短路
copy老师的代码
具体没什么讲的,就放个代码行了。
语法错误谅解一下。。
#include<bits/stdc++.h>
using namespace std;
void SPFA(int x){
memset(dis,0x3f,sizeof dis);
memset(vis,0,sizoef vis);
queue<int> q;
vis[x]=1;dis[x]=0;
q.push(x);
while(!q.empty()){
int now=q.front();
for(int i=head[now];i;i=nxt[i])if(dis[to[i]]>dis[now]+c[i]){
dis[to[i]]=dis[now]+c[i];
if(!vis[dis[to[i]]]) q.push(to[i]),vis[dis[to[i]]]=1;
}
vis[now]=0;q.pop();
}
}
/*
不同点也许是Dij用的是优先队列,而spfa用的是队列?
Dij保证每次取出都是没更新过中的最小值,而spfa通过不断的松弛达到最优解。
还是用Dij比较稳,复杂度有保证,但spfa可以处理负环而Dij不能。
*/
void Dijkstra(int x){
memset(dis,0x3f,sizeof dis);
memset(vis,0,sizeof vis);
priority_queue<pair<int,int> >q;
dis[x]=0;q.push_back(make_pair(0,x));
while(!q.empty()){
int y=q.top().second;q.pop();
if(vis[y])continue;vis[y]=1;
for(int i=head[y];i;i=nxt[i])if(dis[to[i]]>dis[y]+c[i]){
dis[to[i]]=dis[y]+c[i];
q.push(make_pair(-dis[to[i]],to[i]));
}
}
}
void Floyd(){
for(int k=1;k<=n;++k)
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
LCA(最近公共祖先)模板
这个算法用到的的知识点是三体表(ST表)和最近爸爸(Lca最近公共祖先)
首先先要算出每一个点的深度(预处理)
然后对于 \(f\) 数组进行初始化
再进行LCA。lca先将两个结点都变为同意一个深度,如果此时在一个点,那么就返回这一个点(显然是最近公共祖先)。如果不是同一个点,那么就同时网上跳,用倍增来优化,效率很高。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N =5e5+5;
int n,m,s;
vector<int> mp[N<<1];
int dep[N];
int f[N][30];
void add(int x,int y){
mp[x].push_back(y);
}
void dfs(int x){
dep[x] = dep[f[x][0]]+1;
for(auto it:mp[x]){
if(it!=f[x][0]) f[it][0] = x,dfs(it);
}
}
int lca(int x,int y){
if(dep[x] < dep[y]) swap(x,y);
for(int i = log2(dep[x]);~i;--i){
if(dep[f[x][i]] >= dep[y]) x = f[x][i];
}
if(x==y) return x;
for(int i = log2(dep[x]);~i;i--){
if(f[x][i] != f[y][i]) x=f[x][i],y=f[y][i];
}
return f[x][0];
}
int main(){
cin >> n >> m >> s;
for(int i = 1,x,y;i <= n-1;i++){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs(s);
for(int i = 1;(1 << i) <= n;i++){
for(int j = 1;j <= n;++j){
f[j][i] = f[f[j][i-1]][i-1];
}
}
for(int i = 1,x,y;i <= m;i++)
scanf("%d%d",&x,&y),printf("%d\n",lca(x,y));
return 0;
}
二分图
定义:
二分图抽象的说,可以分为两个集合 \(A\),\(B\)。集合 \(A\) 的点只能连到 \(B\),集合 \(B\) 的点也只能连到 \(A\)。
顾名思义,这就是二分图。
二分图是可以不连通的,而且自环不是二分图。
如果有重边需要去除。
判定二分图(染色法)
可以类似洪水填充的思想,如果这个点没有被染过色,那么从这个点开始 dfs 染色。只不过与洪水填充的区别是,洪水填充都是填的一个数。然而这个是 \(1\) 和 \(2\) 间隔着填。如果在填充的时候遇到了矛盾的情况,那么就是不合法的(不是二分图)。
//判定二分图
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m;
vector<int> mp[N];
int vis[N];
void dfs(int x,int color){
for(auto it:mp[x]){
if(!vis[it]){
vis[it] = 3-color;//交替1和2
dfs(it,3-color);
}else if(vis[it] == color){//如果矛盾,那么就不是二分图。
cout<<"No\n";
exit(0);
}
}
}
set<int> st[N];
int main(){
cin >> n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
if(u==v){//自环
cout<<"No\n";
exit(0);
}
if(st[u].find(v) == st[u].end()){//set用来避免重边。
mp[u].push_back(v);
mp[v].push_back(u);
st[u].insert(v);
st[v].insert(u);
}
}
for(int i = 1;i <= n;i++){
if(!vis[i]){//染色填充
dfs(i,1);
}
}
cout<<"Yes";
return 0;
}
接下来,进入正题,讲解如何使用匈牙利算法解决二分图最大匹配的问题。
二分图的最大匹配(匈牙利算法)
首先二分图左边是 \(n1\) 个点,右边是 \(n2\) 个点。其中左边的点只能连到右边的点,右边的点只能连到左边的点,边数为 \(e\)。下文称左边的集合为 \(A\),右边的集合石 \(B\)。
二分图的最大匹配的意思就是:\(A\) 集合的点和\(B\)集合的点可以配对的最大数量。
如图:这里面就有两个最大的匹配数量。(出自洛谷板子样例)
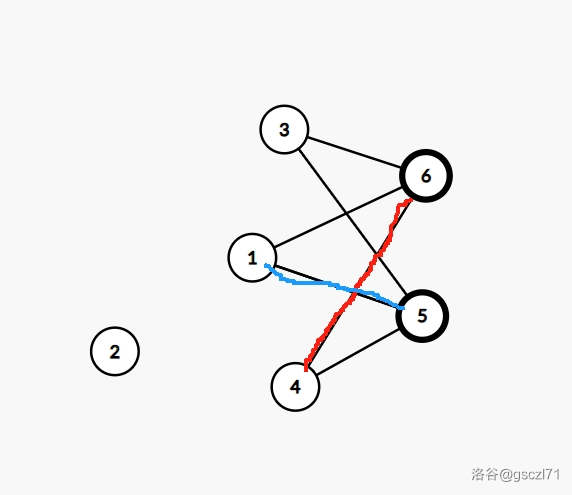
其中红线和蓝线就分别是个匹配。
匈牙利算法呢,就是要找到最大的匹配个数。
思路:
-
遍历 \(A\) 集合,随便选一个 \(B\) 作为配对。
-
如果这个 \(B\) 中的 \(j\) 已经被配对过了,你可以找 \(j\) 之前是和谁配对的,他以前配对的是 \(A\) 中的 \(k\)。那么就让 \(k\) 重新配对,腾个位置给 \(i\) 来配对 \(j\)。因此可以递归下去。
注意:对一个 \(i\) 想要在 \(B\) 中找一个 \(j\) 来配对,肯定不能重复访问这个 \(j\),所以 \(ask_j\) 代表着现在已经像 \(j\) 查询过能否配对了,相当于一个标记。
\(vis_i\) 代表的是 \(B\) 中的 \(i\) 目前和 \(A\) 中的 \(vis_i\) 配对着。
所以这里就使用 dfs 来实现。注意要清空 \(ask\) 数组。因为对于 \(A\) 中的每一个 \(i\),他们的 \(ask\) 都是互相独立的。
时间复杂度是 \(O(n1 \times e + n2)\)。
const int N = 505;
int n1,n2,m;
vector<int> mp[N];
int vis[N],ask[N];
bool dfs(int x){
for(auto it:mp[x]){
if(ask[it])continue;
ask[it]=1;
if(!vis[it] || dfs(vis[it])){
vis[it]=x;
return true;
}
}return false;
}
int match(){
int ans=0;memset(vis,0,sizeof vis);
for(int i = 1;i <= n1;i++){
memset(ask,0,sizeof ask);
if(dfs(i)) ans++;
}return ans;
}
void solve(){
cin>>n1>>n2>>m;
for(int i = 1;i <= m;i++) {int u,v;cin>>u>>v;mp[u].push_back(v);}
cout<<match();
}
本文来自博客园,作者:gsczl71,转载请注明原文链接:https://www.cnblogs.com/gsczl71/p/17852880.html
gsczl71 AK IOI!RP = INF 2024年拿下七级勾!

 浙公网安备 33010602011771号
浙公网安备 33010602011771号