数据结构

数据结构

并查集

并查集的用法：顾名思义，可以合并也可以查询

也就是合并一个集合，查询一个集合。

记录 \(f_i\) 代表第 \(i\) 个点所属集合的祖宗（其实可以代替为这个集合的编号）

具体见代码：

首先建立一个 \(find\) 函数，\(find(x)\) 代表找到这个 \(x\) 所属的祖宗，当 \(x==f_x\) 证明此时其本身就是一个祖宗了，返回自己即可，否则继续迭代 \(find(x)\)。

而此处的f[x]=find(f[x])叫做路径压缩，下一次访问到 \(f_x\) 的时候可以直接忽略后面的操作。当然有些时候不能用路径压缩（可能需要记录路径？

时间复杂度证明比较复杂，个人感觉就在 \(O(1)\) 到 \(O(\log n)\) 之间？（不确定

#include<bits/stdc++.h>
#define ll long long
#define pii pair<int,int>
#define fir first
#define se second
#define ull unsigned long long
#define endl "\n"
using namespace std;
const int N = 1E4+5;
int f[N];
int n,m;
int find(int x){return x==f[x]?x:f[x]=find(f[x]);}
int main(){
    cin>>n>>m;for(int i = 1;i <= n;i++) f[i]=i;
    for(int i = 1;i <= m;i++){
        int op,x,y;
        cin >>op>>x>>y;
        if(op==1){
            if(find(x)!=find(y)) f[find(x)]=find(y);
        }else{
            cout<<(find(x)==find(y)?"Y\n":"N\n");
        }
    }
    return 0;
}

线段树

在一个二叉树上面进行区间操作，区间查询（可以是最大，最小，和，gcd等等）

每一个树上的点都代表着一个区间的值。

流程：

• 建树，将区间为[x,x]的区间设为\(a_x\)
• 对一个区间进行操作，需要遍历到每一个包括这个区间的子节点，显然，时间复杂度会卡到 \(O(n)\)。于是我们想到，可以设计一个标记——lazy tag，可以临时记录目前结点及以下的需要进行什么样的操作，等到进行查询的时候再对下面的结点进行push down 操作，传承lazy tag。显然时间复杂度 \(O(n \log n)\)。
• 进行查询，找到对应区间，不断迭代，然后不断进行pushdown，将懒下标往下传，从而更新要查找的答案。

具体见代码中的注释。

#include <bits/stdc++.h>
using namespace std;
#define ll long long  
const long long maxn = 100005;// 区间的最大长度（根据题目数据要求来定） 
long long n,m,a[maxn];
struct SegmentTree{//结构体 
    long long l,r;//区间左右端点 
    ll sum,mx,mn;//sum为区间和，add为区间记录值 
    long long lazy;//加法的懒标记 
    //mx最大值
    //mn最小值 
}t[maxn*4];//在创建结构体的时候数组大小开最大值的4倍
//这里的maxn就是r-l+1出现的最大值，区间范围上限 
void build (long long p,long long l,long long r){//建树 
//节点编号p指向区间[l,r]
    //存储区间 
    t[p].l = l;//存储左区间 
    t[p].r = r;//存储右区间 
    if(l == r) {//如果区间左端等于右端 那么他就是最下面的节点，也就是叶子节点 
        t[p].sum = a[l];//存最底层叶子的值 
        t[p].mx = a[l];//存最底层叶子的最大值（只有一个值，所以直接存）
        t[p].mn = a[l]; 
        return ;//结束 
    }
    long long mid = (l+r) >> 1;//分治，折半 
    build(p * 2,l,mid);//递归左儿子 
    build(p * 2 + 1,mid + 1,r);//递归右儿子
    //递归结束后即可算出左右儿子的数据
    //再对其进行处理
    //一般分为：求和，最大值，最小值 
    t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum;//区间和
    t[p].mx = max(t[p * 2].mx , t[p * 2 + 1].mx) ;//求最大值
    t[p].mn = min(t[p * 2].mn , t[p * 2 + 1].mn) ;//求最小值
} 
void Add(long long p,long long x){//增加 ，增加编号为p的节点，增加x 懒标记的使用函数 
    t[p].lazy += x;//增加数值，增加的是懒标记 
    t[p].sum += x * (t[p].r - t[p].l + 1);//增加区间和 （通过懒标记） 
}
void pushdown(long long p){//往下进行     （吧懒标记传下去的函数） 
    if(t[p].lazy != 0 && t[p].l != t[p].r){//需要往下传递懒标记，而且不是叶子
         //如果lazy要来标记乘法，那么此处！=0需改为！=1 
        Add(p*2,t[p].lazy);//处理左儿子 
        Add(p*2+1,t[p].lazy);//处理右儿子 
        t[p].lazy = 0;//清空懒标记 
    }
}
void update(long long p,long long l,long long r,long long x){//更新修改值,修改区间 
    //x为增加的值，现存如懒标记 
    pushdown(p); 
    if(l <= t[p].l && t[p].r <= r){//走到头了，找到修改的数里，将其修改，然后return
        //完全覆盖区间直接返回  
        Add(p,x);//将这个值增加 懒标记的操作 
        return ;//回溯 
    }
    long long mid = (t[p].r + t[p].l) >> 1;//计算中间值 
    if(l <= mid) update(p * 2,l,r,x);//判断是否包含左边，往下走 
    if(r > mid) update(p * 2 + 1,l,r,x);//判断是否包含右边，往下走 
    t[p].sum  = t[p * 2].sum + t[p * 2 + 1].sum ;//更新新的值，因为已经走完了下面 
    //因为是加法，所以不能加其他元素进来 
}
void modify(long long p,long long x,long long v){//单点修改，更新修改值 时间复杂度为logN 
    //v为增加值，p为修改的元素的编号 
    if(t[p].l == t[p].r){
        t[p].sum=t[p].mx = t[p].mn=v;
        return;
    }//已经是叶子节点  
    long long mid = (t[p].l + t[p].r )>> 1;//中间点，看是在左儿子还是右儿子那边 
    if(x <= mid) modify(p * 2 ,x ,v);//属于左边还是右边 ，递归修改 
    else modify(p * 2 + 1,x,v);
    t[p].sum = t[p * 2].sum + t[p * 2 + 1].sum;//从下往上传递区间值 
    t[p].mx = max(t[p * 2].mx , t[p * 2 + 1].mx);//从下往上传递区间值 
    t[p].mn = min(t[p * 2].mn , t[p * 2 + 1].mn);//从下往上传递区间值
}
ll query(long long p,long long l,long long r){//区间查询 时间复杂度不会超过2*logN 
    if(l <= t[p].l && t[p].r <= r) return t[p].sum;
    pushdown(p);
    //完全覆盖 若要返回不同数值记载sum可以修改    
    long long mid = (t[p].l + t[p].r) >> 1;
    //做求和操作 
    ll ans = 0;
    if(mid>=l) ans += query(p * 2,l,r);//r与左子节点有重叠 
    if(mid<r) ans+= query(p * 2+1,l,r);//l与右子节点有重叠
    return ans;
    //min和max操作类似
}
int main(){
    cin >> n >> m;    
    for(long long i = 1;i <= n;i++) scanf("%lld",&a[i]);
    build(1,1,n);
    while(m--){
        long long op,x,y,k;
        scanf("%lld",&op);
        if(op == 1){
            scanf("%lld%lld%lld",&x,&y,&k);
            update(1,x,y,k);
        }else{
            scanf("%lld%lld",&x,&y);
            long long ans = query(1,x,y);
            printf("%lld\n",ans);
        }
    }

    return 0;
}

树状数组

“树状数组可以写的题目，线段树也可以写”。但是线段树常数大，不好写。而树状数组小巧精炼，只不过解决的范围小了些。

此处引用 树状数组 - OI Wiki 的一个图片。



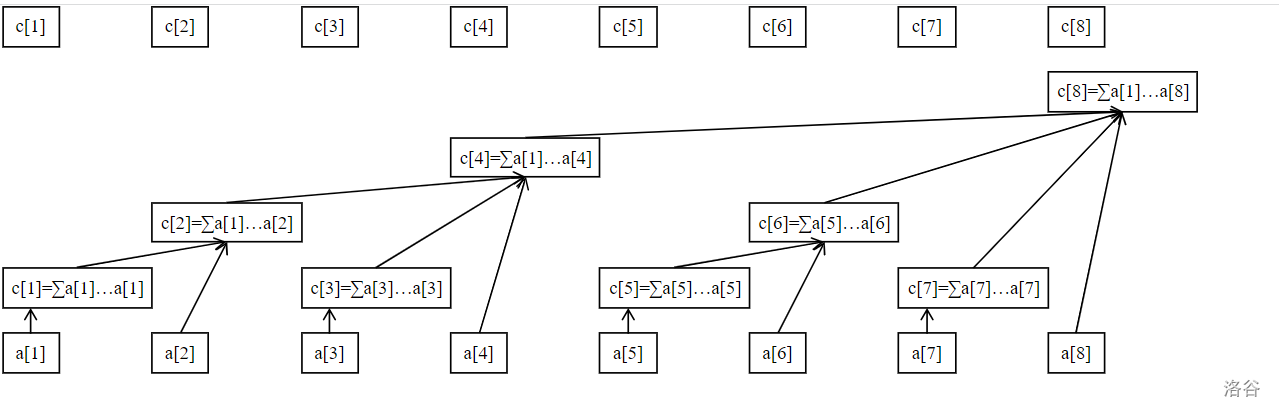
每一个 \(c\) 存储的值就如上图所示。不太好说具体是咋搞来的。

每一个数存储给的下标就不断往后面跳，每一次跳就是跳到后面的一个lowbit（具体来说：“这里注意：lowbit 指的不是最低位 1 所在的位数 \(k\)，而是这个 1 和后面所有 0 组成的 。\(2^k\)”。引用自OIwiki。反正知道往后跳就是了。

然后我们又玄学的得知\(lowbit(x) = x\&(-x)\)

神奇吧？很神奇。知道就好。

通过for循环可以逐步“往后跳”或者“往前跳”由此获得区间求极值或者是累计。

时间复杂度，单次时间复杂度 \(\log n\)，很显然从跳的方式看出来，他是几乎 ×2 ×2 地跳着。

这是一道区间求和的模板。

树状数组2模板原题

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 5e5 + 50;
int n,m; 
int a[N];
int d[N];
int lowbit(int x){
    return x & (-x);
}
void add(int x,int v){
    for(int i =x ;i <= n;i += lowbit(i)) d[i]+=v;
}
int query(int x){
    int ans = 0;
    for(int i = x;i;i -= lowbit(i)) ans+=d[i];
    return ans; 
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++){
        scanf("%d",&a[i]);
        d[i] += a[i]-a[i-1];
        if(i+lowbit(i) <= n) d[i+lowbit(i)] += d[i];
    }
    for(int i= 1;i <= m;i++){
        int op,x,y,k;
        cin >> op >> x;
        if(op==1){
            cin >> y >> k;
            add(x,k);
            add(y+1,-k);
        }
        else{
            cout << query(x) << "\n";
        }
    }
    return 0;
}

ST表

ST表

ST表一般处理：给定 \(n\) 个数，有 \(m\) 个询问，对于每个询问，你需要回答区间 \([l,r]\) 中的最大值。

设：\(f_{i,j}\) 为区间 \([i,i+2^j-1]\) 的最大值。

初始化： \(f_{i,0} = a_i\)

因此可以推导出转移方程 $ f_{i,j} = max(f_{i,j-1},f_{i+2^{j-1},j-1}) $

在输入结束后，可以对其进行预处理。

但是在查询的时候st表不支持修改，只能按原始输入的数组进行查询操作

对于每一个查询 \([l,r]\) , 回答是： $ max([l,l + 2 ^ s -1],[r - 2 ^ s + 1 , r]) $ ,其中 \(s\) 为 $ log_2^{(r-l+1)} $。

这样就能从区间的左端点和右端点分别进行 \(2\) 的整数次方个位置。取 \(max\) 即是整个区间的 \(max\) 。

对于每一次查询是 \(O(1)\) 的。

对于预处理是 \(O(n log n)\) 的。

其实这篇文章应该放到P3865的题解的。可惜不能再提交题解了。

模板：(AC)

#include <iostream>
using namespace std;
#define ll long long
const int N =1e5+5;
int log(int x){
    for(int i = 32;i >= 0;i--){
        if((1<<i) & x) return i;
    }
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
    return x*f;
}
int f[N][30];
int n,m; 
int l,r,t;
int i,j;
int main(){
    n=read();
    m = read();
    for(i = 1;i <= n;++i){
        f[i][0] = read();
    }
    for(j = 1;(1<<j) <= n;++j){
        for(i = 1;i + (1 << j)-1 <= n;++i){
            f[i][j] = max(f[i][j-1],f[i+(1 << (j - 1))][j - 1]);
        }
    }
    for(i = 1;i <= m;++i){
        l=read();
        r=read();
        t=log(r-l+1);
        printf("%d\n",max(f[l][t],f[r - (1 << t) + 1][t]));
    }
    return 0;
}

单调队列

单调队列，顾名思义，单调，就是使得一个数组内单调递增或者单调递减。以来维护任意时间的最大值或最小值。（其实其他值可能可以，不过你要写一个合适的 CMP。

引入的 STL：

这里面需要用到 STL 的 deque。顺便说一下，deque如果插入头部的话，时间复杂度上天，直奔 \(O(n)\) 。所以我们只能尾部插入，然而可以在头部和尾部查询。

如果说卡常的话，换成手写。

废话不多说，进入正题：

假设我们要实时输出长度为 \(k\) 的窗口的最大值。

不妨假设队列头部是最大值。于是就可以得到队列里面是单调（严格）递减的序列。

那么如果此时遍历到的是一个 \(x\) ，那么从队尾插入，如果此时后面的比他小（自然也是比他老旧，其实这么解释很形象，因为已经在队里的元素毕竟是之前插入进来的，所以在未来的某个时刻，可能就是那个队里面的元素不在窗口里面，而 \(x\) 还在。因此我们可以把队列里比 \(x\) 小的（小于等于也行）的踢掉，说白了，就是又老又没有用的把他扔了。

形象的描述结束了，上代码。

每一次的极端值就是队头。不过首先还得先从队头while循环弹出元素，如果这个元素已经不在窗口里了，就不要了。

因此就维护出了区间的极端值。

题目

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll a[1000005];
int main(){
    ll n,k;
    cin >> n >> k;
    for(int i = 1;i <= n;i++){
        scanf("%lld",&a[i]);
    }

    deque<ll> q;

    //求最小值--单调递增
    for(ll i = 1;i <= n;i++){
        while(!q.empty() && a[q.back()] > a[i]){
            q.pop_back();
        }
        q.push_back(i);
        while(!q.empty()&&i-q.front()+1 > k) q.pop_front();
        if(i >= k){
            printf("%lld ",a[q.front()]);
        }
//        for(auto it:q){
//            printf("%lld ",it);
//        }
//        puts("0");
    }
    puts("");
    while(!q.empty()) q.pop_front();
    //求最大值--单调递减
    for(ll i = 1;i <= n;i++){
        while(!q.empty() && a[q.back()] < a[i]){
            q.pop_back();
        }
        q.push_back(i);
        while(!q.empty()&&i-q.front()+1 > k) q.pop_front();
        if(i >= k){
            printf("%lld ",a[q.front()]);
        }
    }

    return 0;
}

二叉堆

其实没什么好讲的，就是priority_queue。

就是每一次 \(\log n\) 地插入查询。维护整体区间的最大值或最小值。

每一次放在最末端，然后依次上浮（通过比较）找到合适的位置。这就是push

每一次从上面堆顶删除掉元素后，元素会变成最小的，下浮，然后使得删除后的序列依然保持着有序。

实现比较简单，还不如直接写优先队列。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6+50;
int n,cnt;
int a[N];
void add(int x){
    a[++cnt] = x;
    int u = cnt;
    while(u >  1){
        int fa = u >> 1;
        if(a[u] >= a[fa]) return ;
        swap(a[u],a[fa]);
        u = fa;
    } 
    return ;
} 
void del(){
    if(cnt < 1)return ;
    a[1] = a[cnt--];
    int u = 1;
    while((u << 1) <= cnt){
        int v= u << 1;
        if(v < cnt && a[v+1] < a[v]) ++v;
        if(a[u] <= a[v]) return ;
        swap(a[u],a[v]);
        u = v;
    }
    return ;
}
int get(){
    return a[1];
}
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++){
        int op;
        cin >> op;
        if(op==1){
            int x;
            cin >> x;
            add(x);
        }else if(op==2){
            cout << get() << "\n";
        }
        else{
            del();
        }
    }

    return 0;
}

Update

• 2023 11 23 初次撰写，整理之前luogu博客的文章。