loj10153二叉苹果树
有一棵二叉苹果树，如果数字有分叉，一定是分两叉，即没有只有一个儿子的节点。这棵树共 N 个节点，标号 1 至 N，树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树，因为树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。
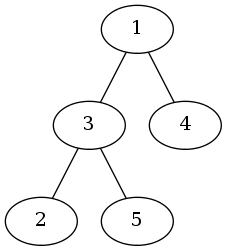
输入格式
第一行两个数 N 和 Q ，N 表示树的节点数，Q 表示要保留的树枝数量。
接下来 N−1 行描述树枝信息，每行三个整数，前两个是它连接的节点的编号，第三个数是这根树枝上苹果数量。
输出格式
输出仅一行，表示最多能留住的苹果的数量。
样例
样例输入
5 2
1 3 1
1 4 10
2 3 20
3 5 20样例输出
21数据范围与提示
对于 100% 的数据，1≤Q≤N≤100,N≠1，每根树枝上苹果不超过 30000 个。
————————————————————————————————————————————————————
树形动归，
开始写的是首先把树变成二叉树，然后动归，记过严重超时，69分，直接在树上进行动归，就可以了，而且时间快很多！！
————————————————————————————————————————————————————
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=105; 4 struct edge 5 { 6 int u,v,w,nxt; 7 }e[maxn<<1]; 8 int head[maxn],js; 9 int n,m; 10 int f[maxn][maxn]; 11 struct node 12 { 13 int w,lc,rc; 14 }tree[maxn]; 15 int lc[maxn],rc[maxn],ww[maxn]; 16 inline void addage(int u,int v,int w) 17 { 18 e[++js].u=u;e[js].v=v;e[js].w=w; 19 e[js].nxt=head[u];head[u]=js; 20 } 21 int dfs(int u,int fa,int s) 22 { 23 if(s==1)return f[u][s]=ww[u]; 24 if(s==0)return 0; 25 if(f[u][s]>0)return f[u][s]; 26 for(int i=head[u];i;i=e[i].nxt) 27 { 28 int v=e[i].v; 29 30 if(v!=fa) 31 { 32 ww[v]=e[i].w; 33 if(lc[u]==0)lc[u]=v; 34 else rc[u]=v; 35 for(int j=0;j<s;++j) 36 { 37 dfs(v,u,j); 38 } 39 } 40 } 41 for(int i=0;i<s;++i) 42 f[u][s]=max(f[u][s],f[lc[u]][i]+f[rc[u]][s-i-1]+ww[u]); 43 return f[u][s]; 44 } 45 void readint(int &x) 46 { 47 x=0; 48 char c=getchar(); 49 for(;c>'9'||c<'0';c=getchar()); 50 for(;c>='0' && c<='9';c=getchar())x=x*10+c-'0'; 51 } 52 int main() 53 { 54 readint(n);readint(m); 55 for(int u,v,w,i=1;i<n;++i) 56 { 57 readint(u);readint(v);readint(w); 58 addage(u,v,w); 59 addage(v,u,w); 60 } 61 dfs(1,0,m+1); 62 cout<<f[1][m+1]; 63 return 0; 64 }
