luogu6038惊吓路径
「ACOI2020」惊吓路径
题目背景

3 年 E 班的同学们赢得了去南方的冲绳小岛的机会,在渚打败了鹰冈之后,他们受杀老师的邀请参加“试胆大会”。
试胆大会在一个黑漆漆的洞窟里面进行。赤羽 業(Akabane Karma)现在和奧田 愛美站在洞窟的门口。突然,業想到了一个事情。。。
题目描述
杀老师告诉过他们,洞窟可以近似地看成 \(n\) 个点的外向树,因为地形原因,所以一个点到另一个点的边是有方向的,且边的方向都是同向的。这棵树的树根为入度为 \(0\) 的点。每个点都有一个惊吓值,给出每个点的惊吓值 \(a_i\)。
杀老师告诉他们,这个洞穴有很多惊吓路径。如果两个节点 \(u,v\) 构成的路径是一条惊吓路径的话,满足以下条件:
-
\(v\) 一定在 \(u\) 的子树中。
-
\(u, v\) 这条路径上的所有的点的惊吓值的或值 \(\geq k\)。
走过一条惊吓路径就会收到杀老师的惊喜大礼。杀老师已经提前准备好了惊喜大礼,但是業当然已经知道杀老师有一些下流的意图,更别说惊喜大礼的数量可能不够!杀老师已经承诺有多少条惊吓路径就有多少个惊喜大礼。業已经通过一些神奇的途径知道了杀老师准备的惊喜大礼的个数,现在他想知道有多少条惊吓路径,也就是杀老师最少需要准备惊喜大礼的个数。如果不够,他就会揭穿杀老师的意图。现在業当然想赚,好好捉弄一下杀老师。所以他作弊提前得到了杀老师的地图,想问这个图里面有多少条惊吓路径?
输入格式
第一行两个整数 \(n,k\)。
第二行 \(n\) 个整数,表示每个点的惊吓值。
接下来 \(n-1\) 行,每行有两个整数 \(u,v\) 表示节点 \(u,v\) 之间有一条有向边,节点 \(u\) 可以到达节点 \(v\),节点 \(v\) 不可以到达节点 \(u\)。
输出格式
一行一个整数,表示这个洞穴的惊吓路径条数。
样例 #1
样例输入 #1
5 10
5 9 6 4 2
3 1
3 4
1 2
1 5
样例输出 #1
2
样例 #2
样例输入 #2
7 5
6 7 4 5 7 8 9
1 2
2 3
2 4
1 5
5 6
5 7
样例输出 #2
16
样例 #3
样例输入 #3
8 5
4 3 2 5 6 7 6 2
1 2
1 5
2 3
2 4
5 6
5 7
6 8
样例输出 #3
16
提示
样例解释 #1
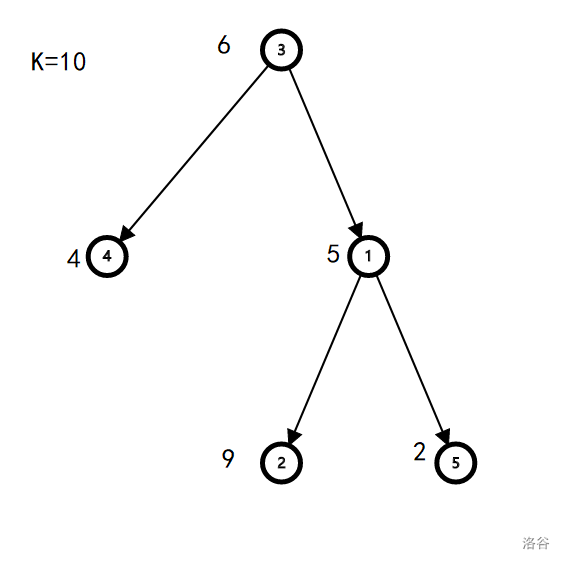
只有两条路径满足条件:
-
\(3\to 1\to 2\),这条路径的所有点的惊吓值的或值是 \(6\operatorname{or}5\operatorname{or}9=15\)。
-
\(1 \to 2\),这条路径的所有点的惊吓值的或值是 \(5\operatorname{or}9=13\)。
数据范围
本题采用捆绑测试。
- Subtask 1(10 points):\(n \leq 5 \times 10^3\),\(k \leq 10^5\)。
- Subtask 2(30 points):对于任意一条边,\(v=u+1\),\(n \leq 10^6\),\(k,a_i \leq 10^9\)。
- Subtask 3(20 points):\(n \leq 10^5\),\(k,a_i \leq 10^9\)。
- Subtask 4(40 points):\(n \leq 5 \times 10^5\),\(k,a_i \leq 10^9\)。
对于 \(100\%\) 的数据,\(1 \leq n \leq 10^6\),\(1 \leq k,a_i \leq 10^9\)。
提示
第四个子任务中的测试点空间 256MB,其余子任务中的测试点空间 128MB。
我没过!!!!题目是并不算难,树上倍增!但是,我没过!!!!我没过!!!!
首先,题中所求是或和,这个不能差分。只能从当前点u向上找到第一个区间或和大于等于K的点v,那么v的深度就是以u点为下届或和大于等于K的点的个数。
怎么快速找到点v,就要用倍增了。f[i][j]就是从i点向上跳\(2^j\)步所有点的或和(实际上是\(s^{j-1}\)步)。
恶心人的是,这个题目卡内存。128M
于是,开到了f[5e5][18],搜索过程中,只是把当前链上的点计算f[][],这样就节省了内存。
然而又4个点不过,以为他们是一条链,而且是1e6个点。
于是单独处理链,试过分块,超时!这个是意料之中的。
于是用线段树,把倍增改成分治,超时。因为要多加一个log,就成了\(n\log^2n\)。
看到题解里面有一个大神,不用这么麻烦,直接开了f[1e6][20]。用手写模拟了深搜。过了。强悍啊!!!
我只能用另一种方法,让倍增中的点三个何为一个,这样就只用三分之一的空间。每个数可能需要单独向上走1、2步,然后再倍增。空间足够了,速度也可以。
然而。还是那两个点,竟然WA!
崩溃了!不写了!!!
不过通过这个题目确实学习了很多的东西!!!
好多的大神啊!!!
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
struct edge
{
int v,nxt;
}e[maxn];
long long ans;
int head[maxn],js;
void addage(int u,int v)
{
e[++js].v=v;e[js].nxt=head[u];head[u]=js;
}
int n,k;
int val[maxn];
int sta[500005],cnt;
int f[500005][18];
void dfs(int u)
{
sta[++cnt]=u;
if(cnt%3==0)
{
int cntt=cnt/3;
f[cntt][0]=val[u]|val[sta[cnt-1]]|val[sta[cnt-2]];
for(int i=1;(1<<i)<=cntt;++i)f[cntt][i]=f[cntt][i-1]|f[cntt-(1<<(i-1))][i-1];
}
int z=0;
if(val[u]>=k)z=cnt;
else
{
int x=cnt,y=0;
while(x%3&&y<k)
{
y|=val[sta[x]];
x--;
}
if(y>=k){z=x+1;}
else
{
int xx=x/3;
if(xx>0)
for(int i=17;i>=0;i--)
{
if(xx-(1<<i)<0)continue;
if((y|f[xx][i])<k){y=(y|f[xx][i]);xx=xx-(1<<i);}
}
x=xx*3;
if(x>0)
{
y|=val[sta[x]];
x--;
while(x%3 && y<k)
{
y|=val[sta[x]];
x--;
}
z=x+1;
}
}
}
ans+=z;
for(int i=head[u];i;i=e[i].nxt)
{
dfs(e[i].v);
}
cnt--;
}
bool rd[maxn];
int main()
{
scanf("%d%d",&n,&k);
bool bz=1;
for(int i=1;i<=n;++i)scanf("%d",val+i);
for(int u,v,i=1;i<n;++i)
{
scanf("%d%d",&u,&v);
addage(u,v);
if(v!=u+1)bz=0;
rd[v]=1;
}
int root;
for(int i=1;i<=n;++i)if(rd[i]==0){root=i;break;}
dfs(root);
cout<<ans<<endl;
return 0;
}



