洛谷5588 小猪佩奇爬树
题目描述
佩奇和乔治在爬♂树。
给定 nn 个节点的树 T(V,E)T(V,E),第 ii 个节点的颜色为 w_iwi,保证有1 \leq w_i \leq n1≤wi≤n。
对于1 \leq i \leq n1≤i≤n,分别输出有多少对点对 (u,v)(u,v),满足 u<vu<v,且恰好经过所有颜色为 ii 的节点,对于节点颜色不为 ii 的其他节点,经过或不经过均可。
树上路径 (u,v)(u,v) 定义为序列 \{f\}{f},满足 f_1=u,f_{|f|}=vf1=u,f∣f∣=v,且 \forall 1 \leq i < |f|∀1≤i<∣f∣,TT 中均存在边 (f_i,f_{i+1})(fi,fi+1),且 \{f\}{f} 中无重复元素,能够证明对于任意点对 (u,v)(u,v),其树上路径唯一。
输入格式
第一行 11 个正整数,表示 nn 。
第二行 nn 个正整数,第 ii 个正整数表示 w_iwi。
之后 n-1n−1 行,每行 22 个正整数 u,vu,v,表示 TT 中存在边 (u,v)(u,v)。
输出格式
共 nn 行,每行 11 个正整数,第 ii 行输出包含所有颜色为 ii 的节点的路径个数。
输入输出样例
4 1 2 2 3 1 2 2 3 3 4
3 4 3 6
10 9 7 4 2 3 4 4 5 8 5 2 1 3 2 4 2 5 2 6 4 7 4 8 1 9 4 10 4
45 35 9 0 1 45 34 9 17 45
说明/提示
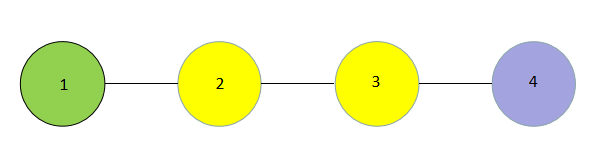
对于第一组样例而言。
对于颜色 11,点对 (1,2),(1,3),(1,4)(1,2),(1,3),(1,4) 满足条件。
对于颜色 22,点对 (1,3),(1,4),(2,3),(2,4)(1,3),(1,4),(2,3),(2,4) 满足条件。
对于颜色 33,点对 (1,4),(2,4),(3,4)(1,4),(2,4),(3,4) 满足条件。
对于颜色 44,由于图中没有颜色为 44 的节点,所以所有点对均满足条件。
数据范围
对于 40\%40% 的数据, n \leq 10^2n≤102
对于 60\%60% 的数据, n \leq 10^3n≤103
对于 100\%100% 的数据, n \leq 10^6n≤106
——————————————————————————
代码是自己写的,思路是哔哩哔哩上一个高手讲的!
第一次发现搜索还可以这样用,不多见!也不好写!这是我在一个搜索中维护东西最多的一次!应该是!
高手的讲解:https://www.bilibili.com/video/av74020427/
——————————————————————————

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e6+10; 4 struct edge 5 { 6 int u,v,nxt; 7 }e[maxn<<1]; 8 int head[maxn],js; 9 int c[maxn],n; 10 void addage(int u,int v) 11 { 12 e[++js].u=u;e[js].v=v; 13 e[js].nxt=head[u];head[u]=js; 14 } 15 int zz[maxn],l[maxn],r[maxn],cnt[maxn],dfn[maxn],ct[maxn],siz[maxn],fat[maxn]; 16 int jss; 17 int f[maxn][21],dep[maxn]; 18 void dfs(int u,int fa) 19 { 20 siz[u]=1;fat[u]=fa; 21 dfn[u]=++jss;dep[u]=dep[fa]+1;f[u][0]=fa; 22 for(int i=1;f[u][i-1];++i)f[u][i]=f[f[u][i-1]][i-1]; 23 if(zz[c[u]]&&dfn[u]>zz[c[u]])ct[c[u]]++; 24 for(int i=head[u];i;i=e[i].nxt) 25 { 26 int v=e[i].v; 27 if(v!=fa) 28 { 29 dfs(v,u); 30 siz[u]+=siz[v]; 31 } 32 } 33 if(zz[c[u]]==0)zz[c[u]]=dfn[u],l[c[u]]=u; 34 if(dfn[u]<=zz[c[u]])ct[c[u]]++; 35 if(ct[c[u]]==cnt[c[u]])r[c[u]]=u; 36 if(zz[c[u]]&&dfn[u]>zz[c[u]])ct[c[u]]--; 37 } 38 int lca(int u,int v) 39 { 40 if(dep[u]<dep[v])swap(u,v); 41 for(int i=20;i>=0;--i)if(dep[f[u][i]]>=dep[v])u=f[u][i]; 42 if(u==v)return u; 43 for(int i=20;i>=0;--i)if(f[u][i]!=f[v][i])u=f[u][i],v=f[v][i]; 44 return f[u][0]; 45 } 46 int main() 47 { 48 scanf("%d",&n); 49 for(int i=1;i<=n;++i)scanf("%d",c+i),cnt[c[i]]++; 50 for(int u,v,i=1;i<n;++i) 51 { 52 scanf("%d%d",&u,&v); 53 addage(u,v); 54 addage(v,u); 55 } 56 dfs(1,0); 57 for(int i=1;i<=n;++i) 58 { 59 if(l[i]==0)printf("%lld\n",(long long)n*(n-1)/2); 60 else if(l[i]==r[i]) 61 { 62 long long ans=2*n-2; 63 int u=l[i]; 64 for(int i=head[u];i;i=e[i].nxt) 65 { 66 int v=e[i].v; 67 if(v==fat[u])ans+=(long long)(n-siz[u])*(siz[u]-1); 68 else ans+=(long long)siz[v]*(n-siz[v]-1); 69 } 70 printf("%lld\n",ans/2); 71 } 72 else if(r[i]==0)puts("0"); 73 else 74 { 75 long long ans; 76 int tp=lca(l[i],r[i]); 77 if(tp==l[i]||tp==r[i]) 78 { 79 if(tp!=l[i])swap(l[i],r[i]); 80 int x=r[i]; 81 for(int j=20;j>=0;--j)if(dep[f[x][j]]>dep[l[i]])x=f[x][j]; 82 ans=(long long)siz[r[i]]*(n-siz[x]); 83 } 84 else ans=(long long)siz[l[i]]*siz[r[i]]; 85 printf("%lld\n",ans); 86 } 87 } 88 return 0; 89 }





