LOJ10015扩散
10015. 「一本通 1.2 练习 2」扩散
题目描述
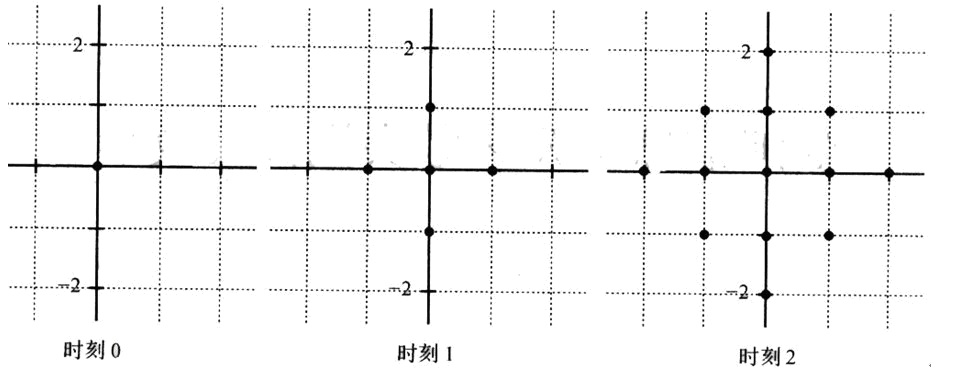
一个点每过一个单位时间就会向 4 个方向扩散一个距离,如图所示:两个点 a 、b 连通,记作e(a,b) ,当且仅当 a、b 的扩散区域有公共部分。连通块的定义是块内的任意两个点 u、v都必定存在路径e(u,a0),e(a0,a1),e(a1,a2)...e(ak,v) 。
给定平面上的 n 个点,问最早什么时候它们形成一个连通块。
输入格式
第一行一个数 n ,以下 n 行,每行一个点坐标。
输出格式
输出仅一个数,表示最早的时刻所有点形成连通块。
样例
数据范围与提示
对于 20% 的数据,满足1<=n<=5,1<=x_i,y_i<=50 ;
对于 100% 的数据,满足1<=n<=50,1<=x_i,y_i<=1e9 。
_______________________________________
二分出最短时间d,那么d时间内每个点扩展d距离,则两点的距离缩短2*d距离,距离小于2*d的点就连同了。
枚举每两个点的距离判断是否小于2d,并用并查集维护。
判断并查集是否合并了n-1次就可以了!
_______________________________________

1 #include<bits/stdc++.h> 2 using namespace std; 3 struct node 4 { 5 int x,y; 6 }ns[55]; 7 int f[55]; 8 int n; 9 int find(int x) 10 { 11 return f[x]==x?x:f[x]=find(f[x]); 12 } 13 void join(int x,int y) 14 { 15 int xx=find(x),yy=find(y); 16 f[xx]=yy; 17 } 18 int dis(int aa,int bb) 19 { 20 node a=ns[aa],b=ns[bb]; 21 int xx,yy; 22 xx=a.x>b.x?a.x-b.x:b.x-a.x; 23 yy=a.y>b.y?a.y-b.y:b.y-a.y; 24 return xx+yy; 25 } 26 bool pd(int d) 27 { 28 d<<=1; 29 int cnt=0; 30 for(int i=1;i<=n;++i)f[i]=i; 31 for(int i=1;i<=n;++i) 32 for(int j=i+1;j<=n;++j) 33 if(dis(i,j)<=d && find(i)!=find(j)) 34 { 35 join(i,j); 36 cnt++; 37 } 38 return cnt==n-1; 39 } 40 int main() 41 { 42 scanf("%d",&n); 43 for(int i=1;i<=n;++i)scanf("%d%d",&ns[i].x,&ns[i].y); 44 int l=1,r=1000000000,ans; 45 while(l<=r) 46 { 47 int mid=(l+r)>>1; 48 if(pd(mid))ans=mid,r=mid-1; 49 else l=mid+1; 50 } 51 cout<<ans; 52 return 0; 53 }





