loj10002喷水装置
长L米,宽W米的草坪里装有N 个浇灌喷头。每个喷头都装在草坪中心线上(离两边各 W/2米)。我们知道每个喷头的位置(离草坪中心线左端的距离),以及它能覆盖到的浇灌范围。
请问:如果要同时浇灌整块草坪,最少需要打开多少个喷头?
输入格式
输入包含若干组测试数据。
第一行一个整数 T表示数据组数;
每组数据的第一行是整数N 、L 和W ;
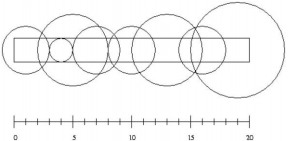
接下来的 N 行,每行包含两个整数,给出一个喷头的位置和浇灌半径(上面的示意图是样例输入第一组数据所描述的情况)。
输出格式
对每组测试数据输出一个数字,表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开也不能浇灌整块草坪,则输出 -1 。
样例
样例输入
3
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1
样例输出
6
2
-1
数据范围与提示
对于100% 的数据N<=15000,
___________________________________________
经典的贪心题目。
贪心的内容:肯定覆盖的越长越好。但是不能按长度排序,而应该从头开始选,同样满足条件的情况下选长的。
方法:首先按照左边界排序,能够覆盖左边界的线段中选择向右覆盖的距离(也就是右边界)最远的,这是需要覆盖的图形的新的左边界就变成的这个“右边界”。然后继续进行,知道全部覆盖。如果中间有区间无法覆盖就输出-1.
题目并不难,但是做的过程中忽略了一点,导致出现错误,那就是有的装置的喷洒半径无法到达草坪的宽度,这种装置可以忽略。
___________________________________________

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=15010; 4 int n,nn,t; 5 double l,w; 6 struct node 7 { 8 double bg,ed; 9 }pt[maxn]; 10 bool cmp(node x,node y) 11 { 12 return x.bg<y.bg; 13 } 14 int ans; 15 double rt; 16 int main() 17 { 18 scanf("%d",&t); 19 while(t--) 20 { 21 scanf("%d%lf%lf",&nn,&l,&w); 22 w/=2; 23 n=0; 24 for(int i=1;i<=nn;++i) 25 { 26 double p,r; 27 scanf("%lf%lf",&p,&r); 28 if(r<=w) continue; 29 ++n; 30 double tmp=sqrt(r*r-w*w); 31 pt[n].bg=p-tmp;pt[n].ed=p+tmp; 32 } 33 sort(pt+1,pt+1+n,cmp); 34 ans=0;rt=0; 35 int cur=1; 36 double tmp=0; 37 bool bz; 38 while(cur<=n) 39 { 40 bz=0; 41 while(cur<=n && pt[cur].bg<=rt) 42 { 43 if(pt[cur].ed>rt) 44 { 45 bz=1; 46 tmp=max(tmp,pt[cur].ed); 47 } 48 ++cur; 49 } 50 51 if(bz==0||tmp==rt) 52 { 53 puts("-1"); 54 break; 55 } 56 ans++,rt=tmp; 57 if(rt>=l)break; 58 } 59 if(rt>l)printf("%d\n",ans); 60 61 } 62 return 0; 63 }





