搜索入门之dfs--经典的迷宫问题解析
今天来谈一下dfs的入门,以前看到的dfs入门,那真的是入门吗,都是把dfs的实现步骤往那一贴,看完是知道dfs的步骤了,但是对于代码实现还是没有概念。今天准备写点自己的心得,真的是字面意思--入门。
DFS,即深度优先搜索,是一种每次搜索都向尽可能深的地方去搜索,到达尽头时再回溯进行其他结点去搜索的搜索策略。形象的说,这是一种“不撞南墙不回头”的策略。
其实也就是遍历,只不过不像一个线性数组的遍历那么直观罢了。说到回溯,每次看到这个词我都得思考一会,到底是怎么用栈进行回溯的呢?今天实际操作了一次bfs,才发现妹的,这个事都是交给编译器去完成的(只要写的是递归形式)...当然了,非递归形式的dfs实现,肯定是要自己做栈的...
迷宫问题
迷宫问题是dfs入门的一个经典问题,这里就以HDOJ 1010 Tempter of Bone 来谈谈如何实际运用dfs。
http://acm.hdu.edu.cn/showproblem.php?pid=1010
题目大意:
S.X.
..X.
..XD
....
给出一个由以上四种符号组成的“迷宫”,‘.’代表可以通行的块,‘X’代表墙不能通过,‘S’代表起点,‘D’代表终点,每秒都必须且只能走一步(上、下、左、右),判断能否恰好在第T秒,到达终点D。其中每次走过的‘.’块都会立刻消失不能再走。
当然了,算法就是dfs了,其实也就是暴力枚举,对走的每一步都进行4个方向上的分支判断,再加上一定的剪枝,舍去一些明显不合题意的结果,以满足时间上的要求。
先贴上代码吧:
1 #include<cstdlib> 2 #include<cstring> 3 #include<iostream> 4 using namespace std; 5 char map[9][9];//输入的迷宫矩阵 6 int dir[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};//4个方向 7 int OK = 0; 8 int N, M, T, si, sj, di, dj; 9 int dfs(int si, int sj, int cnt) 10 { 11 if (si <= 0 || sj <= 0 || si > N || sj > M)//超出边界就说明这条路已经死了,则返回 12 { 13 return 0; 14 } 15 if (si == di && sj == dj && cnt == T)//找到终点就返回,把标志位置为1 16 { 17 OK = 1; 18 } 19 if (OK) 20 { 21 return 1; 22 } 23 int temp = T - cnt - abs(di - si) - abs(dj - sj);//这里就是剪枝,开始没写这里,Time Limit Exceeded了十几次...下面细谈 24 if (temp < 0 || temp & 1) 25 { 26 return 0; 27 } 28 for (int i = 0; i < 4; ++i)//对走到的每个结点都进行四个方向的探索 29 { 30 if (map[si+dir[i][0]][sj+dir[i][1]] != 'X') 31 { 32 map[si+dir[i][0]][sj+dir[i][1]] = 'X';//走过的路不能走,就先置为墙 33 dfs(si+dir[i][0], sj+dir[i][1], cnt + 1); 34 map[si+dir[i][0]][sj+dir[i][1]] = '.';//探索下一条路时,这个结点要恢复成可以走的状态 35 } 36 } 37 return 0; 38 } 39 int main() 40 { 41 while(cin >> N >> M >> T) 42 { 43 int wall = 0; 44 OK = 0; 45 if (N == 0 && M == 0 && T == 0) 46 { 47 break; 48 } 49 for (int i = 1; i <= N; ++i) 50 { 51 for (int j = 1; j <= M; ++j) 52 { 53 cin >> map[i][j];//这里开始还写的scanf("%c", &map[i][j]);蠢的不谈了... 不过可以这样在for(i)的循环里面写 scanf("%s", &map[i]); 54 if (map[i][j] == 'S') 55 { 56 si = i; 57 sj = j; 58 }else if (map[i][j] == 'D') 59 { 60 di = i; 61 dj = j; 62 }else if (map[i][j] == 'X') 63 { 64 wall++; 65 } 66 } 67 } 68 if (N * M - wall <= T)//一个小剪枝 69 { 70 cout << "NO" << endl; 71 continue; 72 } 73 map[si][sj] = 'X'; 74 dfs(si, sj, 0); 75 if (OK) 76 { 77 cout << "YES" << endl; 78 }else 79 { 80 cout << "NO" << endl; 81 } 82 } 83 return 0; 84 }
先借助代码谈一下dfs的过程:
从S开始,i = 0,往右探索,只要没有return,就一直往右走,return了就回溯,回溯的过程呢,就是从i = 0转到i = 1了,这就是回溯的实现过程...
一个小技巧,初始化这个迷宫矩阵的时候,i = 0 , j = 0, i = n + 1, j = m + 1都进行初始化,但是不存储数据,这样相当于在迷宫外面的四面都加上了墙,这样在dfs过程中就不用判断是否出界了...
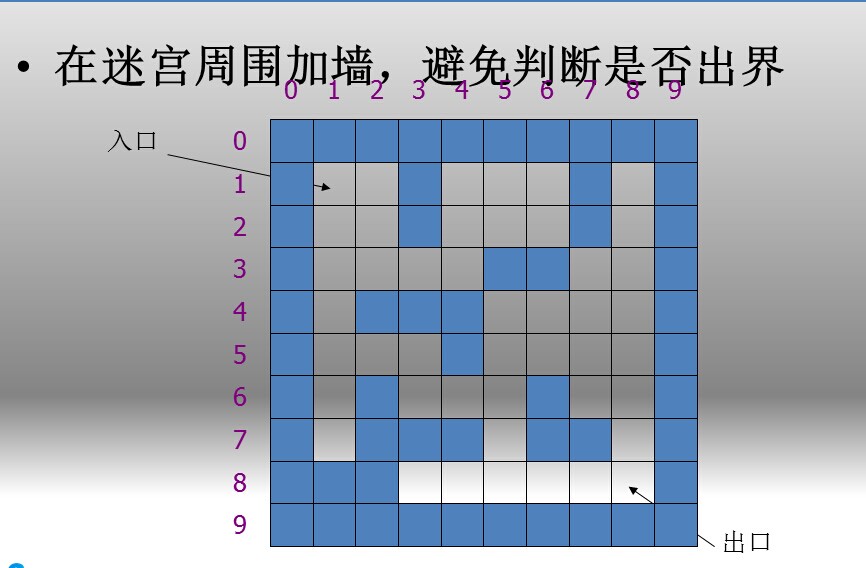
下面谈一下剪枝:
1、如果可走的块数小于T,则肯定不能到达,这就是main()中的那个小剪枝
2、奇偶性剪枝:
所以当遇到从 0 走向 0 但是要求时间是奇数的,或者, 从 1 走向 0 但是要求时间是偶数的 都可以直接判断不可达!
这就是dfs中那个剪枝,也就是最主要的剪枝,其中用了&与运算来判断是不是偶数...
提醒:
算法中最基本和常用的是搜索,这里要说的是,有些初学者在学习这些搜索基本算法是不太注意剪枝,这是十分不可取的,因为所有搜索的题目给你的测试用例都不会有很大的规模,你往往察觉不出程序运行的时间问题,但是真正的测试数据一定能过滤出那些没有剪枝的算法。
实际上参赛选手基本上都会使用常用的搜索算法,题目的区分度往往就是建立在诸如剪枝之类的优化上了。 ”


