数据结构7.1_图的定义和术语

本文参考链接： 

图的定义和各种术语总结：https://blog.csdn.net/eyishion/article/details/53234255

 

1.1 图的定义

图（Graph）中的数据元素通常称做顶点（Vertex）。两个顶点之间的连线叫做边（Edge）。

V是顶点的有穷非空集合。

在图中任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示。

VR是两个顶点之间关系的集合，也是边的集合。

所以图是顶点的有穷非空集合和顶点之间边的集合组成的。

通常表示为:G(V,E),G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

 

1.2 图的方向性

按照有无方向，还可以把图分为无向图和有向图。

无向边：若顶点A到顶点B的边没有方向，称这条边为无向边，用无序偶对(A,B)或(B,A)表示。

有向边：若顶点A到顶点B的边有方向，称这条边为有向边，也称为弧(Arc)，用有序对 < B, A >表示；B表示弧尾，A表示弧头 

弧用来特指有向边；

 

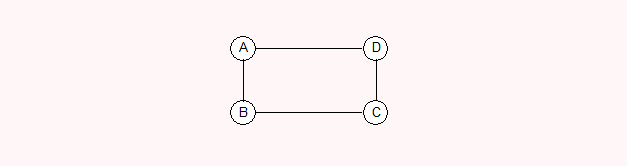
1.3 完全图

无向完全图
在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。
含有n个顶点的无向完全图有n * (n-1)/2条边。下面是一个无向完全图

4个顶点，6条无向边，每个顶点对应3条边 ，一共4个顶点 总共 4*3，每个顶点对应的边都重复计算了一次，所以整体要除以2。
对于n各 顶点和e条边的无向图满足：0<=e <= n(n-1)/2

 

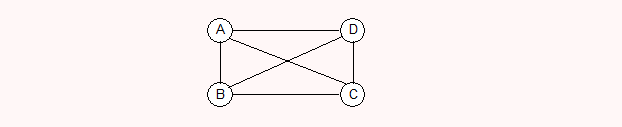
有向完全图
在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。
含有n个顶点的无向完全图有n * (n-1)条边。下面是一个有向完全图

4个顶点，12条弧，一共4个顶点 总共 4*3。

 

1.4 稀疏图

按照弧或边的多少，分为稀疏图和稠密图； 
若边或弧的个数e<=NlogN(N是顶点的个数)，称为系数图，否则称为稠密图； 

 

1.5 网

按照边或弧是否带权，其中带权的图统称为网。 
有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权。 
有向网中弧带权的图叫做有向网； 
无向网中边带权的图叫做无向网； 
比如下图就是一个无向图 

 

1.6 顶点和边的关系

关键词：邻接点、 度、 入度、 出度
对于无向图，假若顶点v和顶点w之间存在一条边，则称顶点v和顶点w互为邻接点，边(v,w)和顶点v和w相关联。
顶点v的度是和v相关联的边的数目，记为TD(v);

上面这个无向图G1，A和B互为邻接点，A和D互为邻接点，B和C互为邻接点，C和D互为邻接点;
A的度是2,B的度是2,C的度是2,D的度是2;所有顶点度的和为8，而边的数目是4；
图中边的数目e = 各个顶点度数和的一半。
对于有向图来说，与某个顶点相关联的弧的数目称为度(TD)；以某个顶点v为弧尾的弧的数目定义为顶点v的出度(OD)；以顶点v为弧头的弧的数目定义为顶点的入度(ID)
度(TD) = 出度(OD) + 入度(ID);

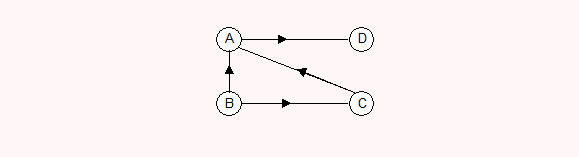
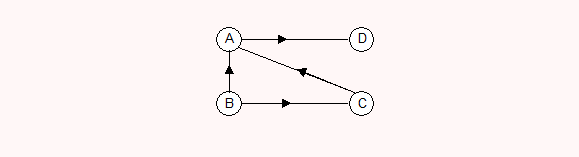
比如上面有向图，
A的度为3 ，A的入度 2，A的出度是1
B的度为2 ，B的入度 0，B的出度是2
C的度为2 ，C的入度 1，C的出度是1
D的度为1 ，D的入度 1，D的出度是0
所有顶点的入度和是4，出度和也是4，而这个图有4个弧
所以 有向图的弧 e = 所有顶点入度的和 = 所有顶点出度的和

 

1.8 路径

关键词：路径 路径长度 简单路径 回路 (环) 简单回路(简单环)
设图G=(V，{E})中的一个顶点序列{u=Fi0,Fi1,Fi2,….Fim=w}中，(Fi,j-1,Fi,j)∈E 1 ≤j ≤m,则称从顶点u到顶点w之间存在一条路径，路径上边或弧的数目称作路径长度，
若路径中的顶点不重复出现的路径称为简单路径
若路径中第一个顶点到最后一个顶点相同的路径称为回路或环
若路径中第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环
比如下图 ：

从B 到 D 中顶点没有重复出现 ，所以是简单路径 ，边的数目是2，所以路径长度为 2。 

图1和图2都是一个回路(环),图1中出了第一个顶点和最后一个顶点相同之外，其余顶点不相同，所以是简单环(简单回路)，图2，有与顶点C重复就不是一个简单环了；

 

1.9 连通图

连通图
在无向图G(V,{E})中，如果从顶点V到顶点W有路径，则称V和W是连通的。如果对于图中任意两个顶点Vi、Vj∈V,Vi和Vj都是连通的，则称G是连通图。
如下图所示：

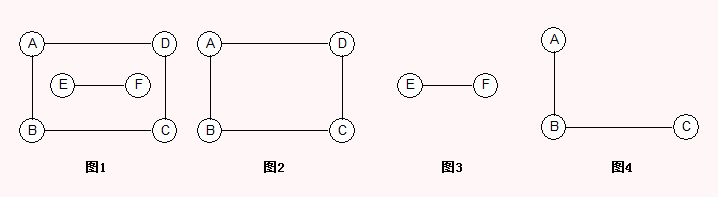
图1，顶点A到顶点E就无法连通，所以图1不是连通；图2，图3，图4属于连通图；

连通分量
若无向图为非连通图，则图中各个极大连通子图称作此图的连通分量；

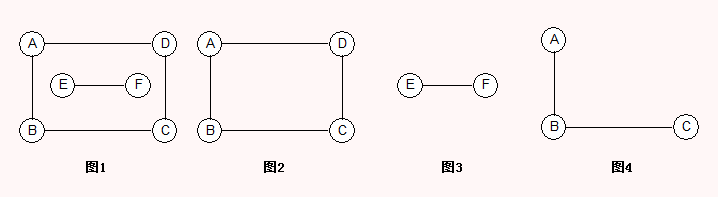
图1是无向非连通图，由两个连通分量，分别是图2和图3。图4尽管也是图1的子图，但是它不满足极大连通，也就说极大连通应当是包含ABCD四个顶点，比如图2那样；

强连通图
在有向图G(V,{E})中，如果对于每一对Vi ,Vj∈V,Vi≠Vj,从Vi到Vj和从Vj到Vi都存在有向路径,则称G是强连通图。

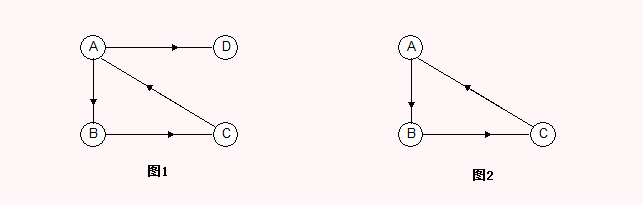
图1不是强连通图因为D到A不存在路径，图2属于强连通图。

强连通分量
若有向图不是强连通图，则图中各个极大强连通子图称作此图的强连通分量；

图1不是强连通图，但是图2是图1的强连通子图，也就是强连通分量；

 

 

1.10 生成树和生成森林
生成树
假设一个连通图有n个顶点和e条边，其中n-1条边和n个顶点构成一个极小连通子图，称该极小连通子图为此连通图的生成树；

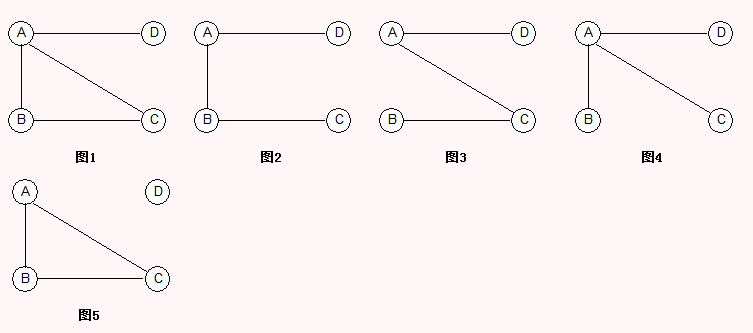
图1是一个连通图含有4个顶点和4条边，图2，图3，图4含有3条边和4个顶点，构成了一个极小连通图子图，也称为生成树，为什么是极小连通子图，因为图2，图3，图4中少一条边都构不成一个连通图，多一条边就变成一个回路(环)，所以是3条边和4个顶点构成的极小连通子图。图5尽管也是3个边4个顶点，但不是连通图。

生成森林
如果一个有向图恰有一个顶点的入度为0，其余顶点的入度为1，则是一颗有向树；
入度为0，相当于根节点，入度为1，相当于分支节点；，比如下面的有向图就是一个有向树

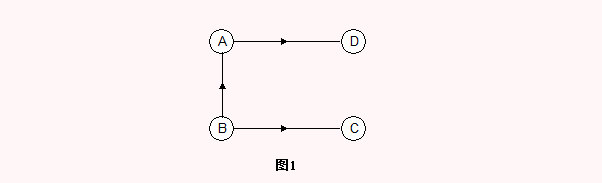
顶点B的入度是0，其余顶点的入度是1；

一个有向图的生成森林由若干颗有向树组成，含有图中全部顶点，但有足以构成若干颗不相交的有向树的弧；

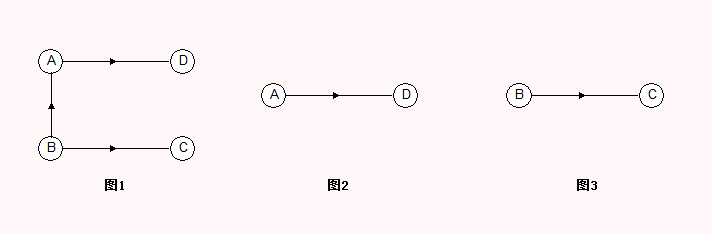
有向图1去掉一些弧后分解成2颗有向树，图2和图3，这两颗树就是有向图图1的生成森林；