一个21行C#代码实现的神经网络
一个21行C#代码实现的神经网络
2017年12月16日 22:09:01 liaogaobo2008 阅读数 2665
网上有个经典教程:叫【一个 11行 Python 代码实现的神经网络】,原文链接:http://python.jobbole.com/82758。闲来无聊, 我们不用任何第三方的库,全部用C#实现它,我花1天多时间写的,主代码也就20行左右(自己写的矩阵类肯定不算再内啦),收敛效果是非常好!模仿别人一下,我也就叫它《一个21行C#代码实现的神经网络》。希望和大家一起研究学习。
写本文的目的是严格弄点神经网络前向传播和反向传播的各个技术计算细节,数学推导公式大家参考博文:http://www.cnblogs.com/charlotte77/p/5629865.html
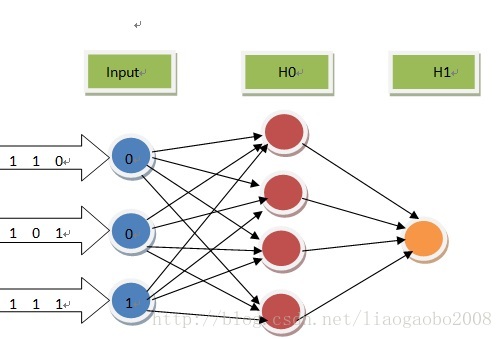
神经网络结构图
主代码如下:
double[,] X = new double[4, 3] { { 0, 0, 1 }, { 1, 1, 1 }, { 1, 0, 1 }, { 0, 1, 1 } };
double[,] y = new double[4, 1] { { 0 }, { 1 }, { 1 }, { 0 } };
Matrix MatX = new Matrix(X);
Matrix MatY = new Matrix(y);
Matrix syn0 = new Matrix(3, 4, true);
Matrix syn1 = new Matrix(4, 1, true);
Matrix L1, L1_Delta;
Matrix L2 = null, L2_Delta;
Matrix L2_Err, L1_Err;
for (long i = 0; i < 9000; i++)
{
L1 = (MatX * syn0).Nonlin(); //l1 = nonlin(np.dot(l0,syn0))
L2 = (L1 * syn1).Nonlin(); //l2 = nonlin(np.dot(l1,syn1))
L2_Err = MatY - L2; //L2_error = y - l2
L2_Delta = L2_Err ^ L2.Derivative(); //l2_delta = l2_error*nonlin(l2,deriv=True)
L1_Err = L2_Delta * syn1.T; //l1_error = l2_delta.dot(syn1.T)
L1_Delta = L1_Err ^ L1.Derivative(); //l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 = syn1 + L1.T * L2_Delta * 0.01;//l1.T.dot(l2_delta)
syn0 = syn0 + MatX.T * L1_Delta * 0.01;//l0.T.dot(l1_delta)
}
Console.WriteLine(L2.ToString());
Console.WriteLine(syn0.ToString());
Console.WriteLine(syn1.ToString());- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
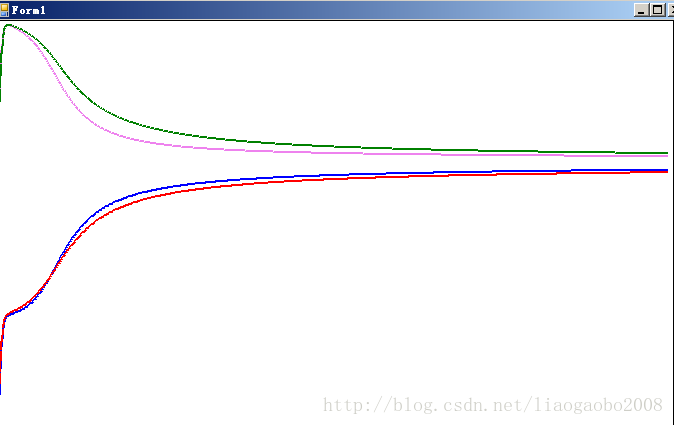
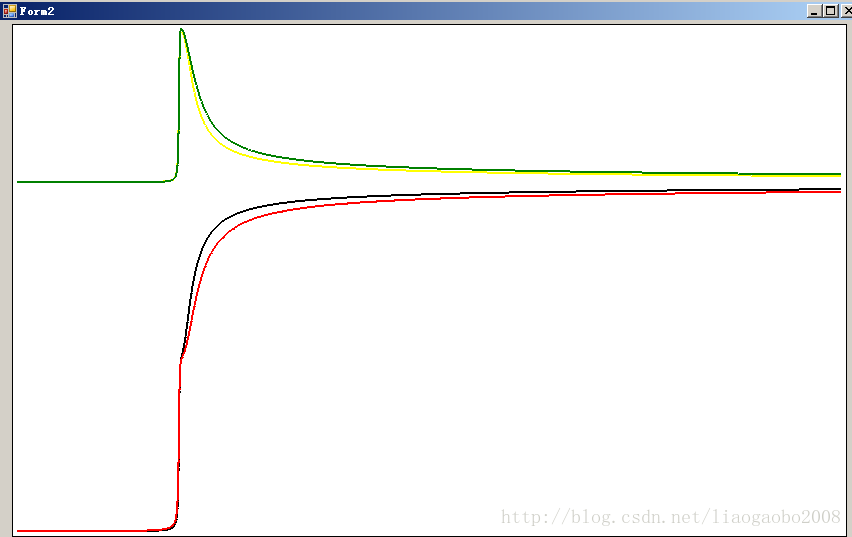
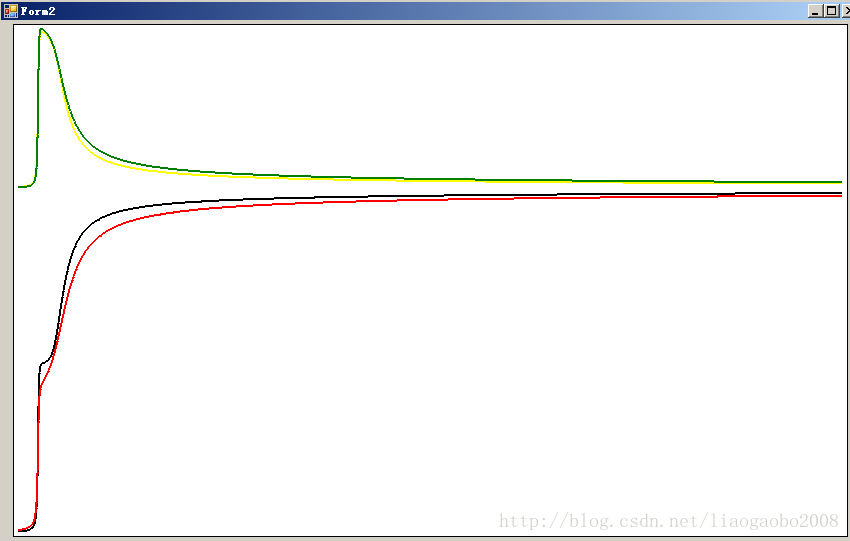
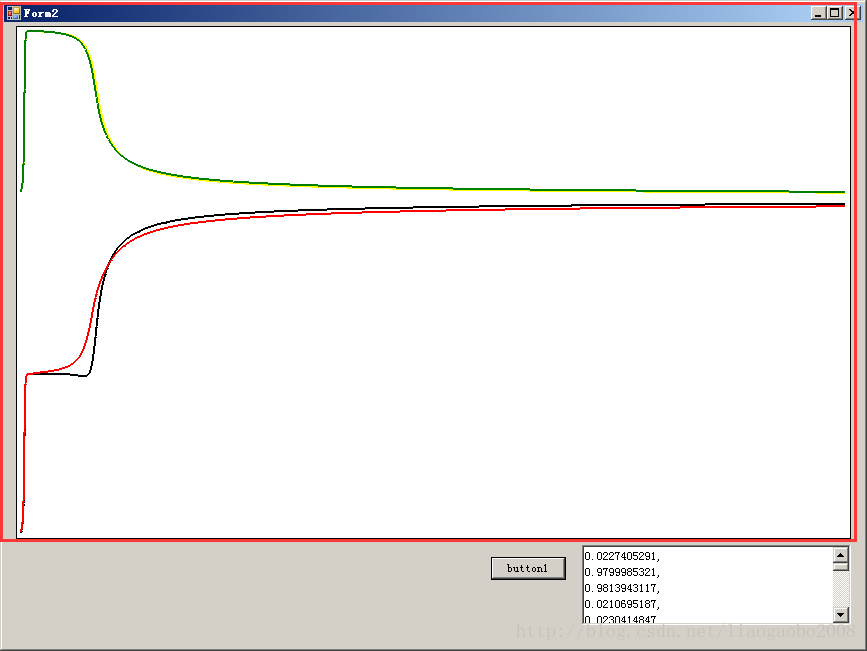
收敛过程如下图,4根不同颜色的线条对应4个样本的收敛过程,可以看出他们都逐渐归到Y=0处(即X轴)
从上几个图可以看出,随着学习次数的增加,我们距离样本的目标越来越近
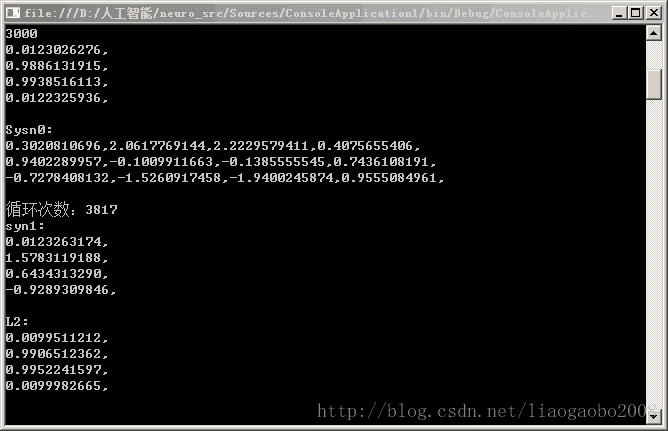
*最终输出结果如下图
Matrix矩阵实类
public class Matrix
{
public double[,] Mat;
private long _m, _n;
public long M
{
get
{
return _m;
}
private set
{
_m = value;
}
}
public long N
{
get
{
return _n;
}
private set
{
_n = value;
}
}
protected static Random rand = new Random((int)DateTime.Now.Ticks);
public Matrix(long m, long n, bool isRandValue=false)
{
_m = m;
_n = n;
Mat = new double[m, n];
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (isRandValue)
Mat[i, j] = rand.NextDouble();
else Mat[i, j] = 0;
}
public Matrix(double[,] m)
{
_m = m.GetLongLength(0);
_n = m.GetLongLength(1);
Mat = m;
}
public static Matrix operator +(Matrix M1, Matrix M2)
{
if (M1.M != M2.M
|| M1.N != M1.N)
throw new Exception("矩阵不符合运算条件,2个矩阵必须完全一样的行和列");
Matrix result = new Matrix(M1.M, M1.N);
for (int i = 0; i < M1.M; i++)
for (int j = 0; j < M1.N; j++)
{
result.Mat[i, j] = M1.Mat[i, j] + M2.Mat[i, j];
}
return result;
}
public static Matrix operator -(Matrix M1, Matrix M2)
{
if (M1.M != M2.M
|| M1.N != M1.N)
throw new Exception("矩阵不符合运算条件,2个矩阵必须完全一样的行和列");
Matrix result = new Matrix(M1.M, M1.N);
for (int i = 0; i < M1.M; i++)
for (int j = 0; j < M1.N; j++)
{
result.Mat[i, j] = M1.Mat[i, j] - M2.Mat[i, j];
}
return result;
}
public static Matrix operator ^(Matrix M1, Matrix M2)
{
if (M1.M != M2.M
|| M1.N != M1.N)
throw new Exception("矩阵不符合运算条件,2个矩阵必须完全一样的行和列");
Matrix result = new Matrix(M1.M, M1.N);
for (int i = 0; i < M1.M; i++)
for (int j = 0; j < M1.N; j++)
{
result.Mat[i, j] = M1.Mat[i, j]* M2.Mat[i, j];
}
return result;
}
public static Matrix operator *(Matrix M1, Matrix M2)
{
long m = M1.Mat.GetLongLength(0);
long jW = M1.Mat.GetLongLength(1);
long iH = M2.Mat.GetLongLength(0);
long n = M2.Mat.GetLongLength(1);
if (jW != iH)
throw new Exception("矩阵不符合运算条件,W的行不等于H的列");
Matrix result = new Matrix(m, n);
for (int i = 0; i < m; i++)//W的行数
{
for (int j = 0; j < n; j++)//H的列数
{
for (int k = 0; k < jW; k++)
{
result.Mat[i, j] += M2.Mat[k, j] * M1.Mat[i, k];
}
}
}
return result;
}
public static Matrix operator *(Matrix M1, double ratio)
{
long m = M1.Mat.GetLongLength(0);
long n = M1.Mat.GetLongLength(1);
Matrix result = new Matrix(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
result.Mat[i, j] = M1.Mat[i, j] * ratio;
return result;
}
public Matrix Nonlin()
{
Matrix result = new Matrix(M,N);
for (int i = 0; i < M; i++)
for (int j = 0; j < N; j++)
result.Mat[i, j] = Sigmoid(Mat[i, j]);
return result;
}
public Matrix Derivative()
{
Matrix result = new Matrix(M, N);
for (int i = 0; i < M; i++)
for (int j = 0; j < N; j++)
result.Mat[i, j] = Derivative(Mat[i, j]);
return result;
}
public double Sigmoid(double x)
{
return (1 / (1 + Math.Exp(-3 * x)));
}
//求导
public double Derivative(double x)
{
return (3 * x * (1 - x));
}
public Matrix T
{
get
{
Matrix result= new Matrix(N, M);
//新矩阵生成规则: b[i,j]=a[j,i]
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
result.Mat[i, j] = this.Mat[j, i];
}
}
return result;
}
}
public override string ToString()
{
StringBuilder sbd = new StringBuilder();
for (int i = 0; i <this.M; i++)
{
for (int j = 0; j < this.N; j++)
{
sbd.Append(Mat[i, j].ToString("N10"));
sbd.Append(",");
}
sbd.AppendLine();
}
return sbd.ToString();
}
}