数据结构 Hash表（哈希表）

数据结构 Hash表（哈希表）

2018年05月20日 01:23:34 洌冰 阅读数 14963

 版权声明：本文为博主原创文章，转载请注明出处 https://blog.csdn.net/u011109881/article/details/80379505

参考链接：数据结构（严蔚敏）

一、什么是Hash表

要想知道什么是哈希表，那得先了解哈希函数

哈希函数

对比之前博客讨论的二叉排序树 二叉平衡树 红黑树 B B+树，它们的查找都是先从根节点进行查找，从节点取出数据或索引与查找值进行比较。那么，有没有一种函数H，根据这个函数和查找关键字key，可以直接确定查找值所在位置，而不需要一个个比较。这样就**“预先知道”**key所在的位置，直接找到数据，提升效率。 
即 
地址index=H（key） 
说白了，hash函数就是根据key计算出应该存储地址的位置，而哈希表是基于哈希函数建立的一种查找表

二、哈希函数的构造方法

根据前人经验，统计出如下几种常用hash函数的构造方法： 
直接定制法 
哈希函数为关键字的线性函数如 H（key）=a*key+b 
这种构造方法比较简便，均匀，但是有很大限制，仅限于地址大小=关键字集合的情况 
使用举例： 
假设需要统计中国人口的年龄分布，以10为最小单元。今年是2018年，那么10岁以内的分布在2008-2018，20岁以内的分布在1998-2008……假设2018代表2018-2008直接的数据，那么关键字应该是2018，2008，1998…… 
那么可以构造哈希函数H（key）=（2018-key）/10=201-key/10 
那么hash表建立如下

index	key	年龄	人数（假设数据）
0	2018	0-10	200W
1	2008	10-20	250W
2	1998	20-30	253W
3	1988	30-40	300W
……

数字分析法 
假设关键字集合中的每个关键字key都是由s位数字组成（k1,k2,……,knk1,k2,……,kn）,分析key中的全体数据，并从中提取分布均匀的若干位或他们的组合构成全体

使用举例 
我们知道身份证号是有规律的，现在我们要存储一个班级学生的身份证号码，假设这个班级的学生都出生在同一个地区，同一年，那么他们的身份证的前面数位都是相同的，那么我们可以截取后面不同的几位存储，假设有5位不同，那么就用这五位代表地址。 
H（key）=key%100000 
此种方法通常用于数字位数较长的情况，必须数字存在一定规律，其必须知道数字的分布情况，比如上面的例子，我们事先知道这个班级的学生出生在同一年，同一个地区。 
平方取中法 
如果关键字的每一位都有某些数字重复出现频率很高的现象，可以先求关键字的平方值，通过平方扩大差异，而后取中间数位作为最终存储地址。 
使用举例 
比如key=1234 1234^2=1522756 取227作hash地址 
比如key=4321 4321^2=18671041 取671作hash地址 
这种方法适合事先不知道数据并且数据长度较小的情况 
折叠法 
如果数字的位数很多，可以将数字分割为几个部分，取他们的叠加和作为hash地址 
使用举例 
比如key=123 456 789 
我们可以存储在61524，取末三位，存在524的位置 
该方法适用于数字位数较多且事先不知道数据分布的情况 
除留余数法用的较多 
H（key）=key MOD p （p<=m m为表长） 
很明显，如何选取p是个关键问题。

使用举例 
比如我们存储3 6 9，那么p就不能取3 
因为 3 MOD 3 == 6 MOD 3 == 9 MOD 3 
p应为不大于m的质数或是不含20以下的质因子的合数，这样可以减少地址的重复（冲突）

比如key = 7，39，18，24，33，21时取表长m为9 p为7 那么存储如下

index	0	1	2	3	4	5	6	7	8
key	7	21（冲突后移）		24	4	18（冲突后移）	33冲突后移）

随机数法 
H（key） =Random（key） 
取关键字的随机函数值为它的散列地址

hash函数设计的考虑因素

1.计算散列地址所需要的时间（即hash函数本身不要太复杂） 
2.关键字的长度 
3.表长 
4.关键字分布是否均匀，是否有规律可循 
5.设计的hash函数在满足以上条件的情况下尽量减少冲突

三、哈希冲突

即不同key值产生相同的地址，H（key1）=H（key2） 
比如我们上面说的存储3 6 9，p取3是 
3 MOD 3 == 6 MOD 3 == 9 MOD 3 
此时3 6 9都发生了hash冲突

哈希冲突的解决方案

不管hash函数设计的如何巧妙，总会有特殊的key导致hash冲突，特别是对动态查找表来说。 
hash函数解决冲突的方法有以下几个常用的方法 
1.开放定制法 
2.链地址法 
3.公共溢出区法 
建立一个特殊存储空间，专门存放冲突的数据。此种方法适用于数据和冲突较少的情况。 
4.再散列法 
准备若干个hash函数，如果使用第一个hash函数发生了冲突，就使用第二个hash函数，第二个也冲突，使用第三个…… 
重点了解一下开放定制法和链地址法

开放定制法

首先有一个H（key）的哈希函数 
如果H（key1）=H（keyi） 
那么keyi存储位置Hi=(H(key)+di)MODmHi=(H(key)+di)MODmm为表长 
didi有三种取法 
1）线性探测再散列 
di=c∗idi=c∗i 
2）平方探测再散列 
di=12,−12,22,−22di=12,−12,22,−22…… 
3）随机探测在散列（双探测再散列） 
didi是一组伪随机数列 
注意 
增量di应该具有以下特点（完备性）：产生的Hi（地址）均不相同，且所产生的s（m-1）个Hi能覆盖hash表中的所有地址 
* 平方探测时表长m必须为4j+3的质数（平方探测表长有限制） 
* 随机探测时m和di没有公因子（随机探测di有限制）

三种开放定址法解决冲突方案的例子

废话不多说，上例子就明白了 
有一组数据 
19 01 23 14 55 68 11 86 37要存储在表长11的数组中，其中H（key）=key MOD 11 
那么按照上面三种解决冲突的方法，存储过程如下： 
（表格解释：从前向后插入数据，如果插入位置已经占用，发生冲突，冲突的另起一行，计算地址，直到地址可用，后面冲突的继续向下另起一行。最终结果取最上面的数据（因为是最“占座”的数据）） 
线性探测再散列 
我们取di=1，即冲突后存储在冲突后一个位置，如果仍然冲突继续向后

index	0	1	2	3	4	5	6	7	8	9	10
key	55	1		14					19	86
		23冲突	23
			68冲突	68冲突	68
	11冲突	11冲突	11冲突	11冲突	11冲突	11
					37冲突	37冲突	37
最终存储结果	55	1	23	14	68	11	37		19	86

平方探测再散列

index	0	1	2	3	4	5	6	7	8	9	10
key	55	1		14	37				19	86
		23冲突	H（23）+1
		H（68）-1冲突	68冲突	H（68）+1冲突			H（68）+4
	11冲突	H（11）-1冲突									H（11）+1
最终存储结果	55	1	23	14	37		68		19	86	11

随机探测在散列（双探测再散列） 
发生冲突后 
H（key）‘=(H(key)+di)MOD m 
在该例子中 
H（key）=key MOD 11 
我们取di=key MOD 10 +1 
则有如下结果：

index	0	1	2	3	4	5	6	7	8	9	10
key	55	1	68	14					19	86
		23冲突				H（23）+3+1
	11冲突		H（11）+1+1冲突		H（11）+1+1+1+1
	（H（37）+8）模11冲突				37冲突			（H（37）+8+8+8）模11		（H（37）+8+8）模11冲突
最终存储结果	55	1	68	14	23		11	37	19	86

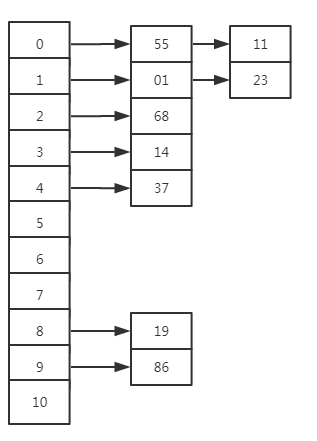
链地址法

产生hash冲突后在存储数据后面加一个指针，指向后面冲突的数据 
上面的例子，用链地址法则是下面这样： 

四、hash表的查找

查找过程和造表过程一致，假设采用开放定址法处理冲突，则查找过程为： 
对于给定的key，计算hash地址index = H（key） 
如果数组arr【index】的值为空 则查找不成功 
如果数组arr【index】== key 则查找成功 
否则 使用冲突解决方法求下一个地址，直到arr【index】== key或者 arr【index】==null

hash表的查找效率

决定hash表查找的ASL因素： 
1）选用的hash函数 
2）选用的处理冲突的方法 
3）hash表的饱和度，装载因子 α=n/m(n表示实际装载数据长度 m为表长) 
一般情况，假设hash函数是均匀的，则在讨论ASL时可以不考虑它的因素 
hash表的ASL是处理冲突方法和装载因子的函数 
前人已经证明，查找成功时如下结果： 
 
可以看到无论哪个函数，装载因子越大，平均查找长度越大，那么装载因子α越小越好？也不是，就像100的表长只存一个数据，α是小了，但是空间利用率不高啊，这里就是时间空间的取舍问题了。通常情况下，认为α=0.75是时间空间综合利用效率最高的情况。

上面的这个表可是特别有用的。假设我现在有10个数据，想使用链地址法解决冲突，并要求平均查找长度<2 
那么有1+α/2 <2 
α<2 
即 n/m<2 (n=10) 
m>10/2 
m>5 即采用链地址法，使得平均查找长度< 2 那么m>5

之前我的博客讨论过各种树的平均查找长度，他们都是基于存储数据n的函数，而hash表不同，他是基于装载因子的函数，也就是说，当数据n增加时，我可以通过增加表长m，以维持装载因子不变，确保ASL不变。 
那么hash表的构造应该是这样的： 

五、hash表的删除

首先链地址法是可以直接删除元素的，但是开放定址法是不行的，拿前面的双探测再散列来说，假如我们删除了元素1，将其位置置空，那 23就永远找不到了。正确做法应该是删除之后置入一个原来不存在的数据，比如-1