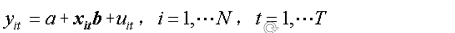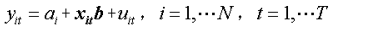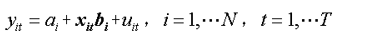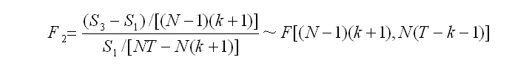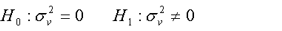R语言-面板数据分析步骤及流程-

面板数据分析步骤及流程-R语言

2016年08月16日 16:49:55 饭饭认认米 阅读数 47093 文章标签： r语言面板数据分析预测 更多

分类专栏： R语言 预测模型

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/fanfanrenrenmi/article/details/52222728

面板数据

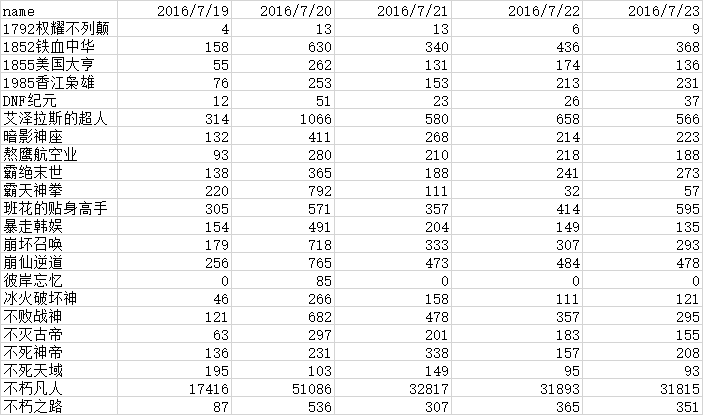
面板数据（Panel Data），也成平行数据，具有时间序列和截面两个维度，整个表格排列起来像是一个面板。 
面板数据举例： 

模型说明及分析步骤

1、首先确定解释变量和因变量； 
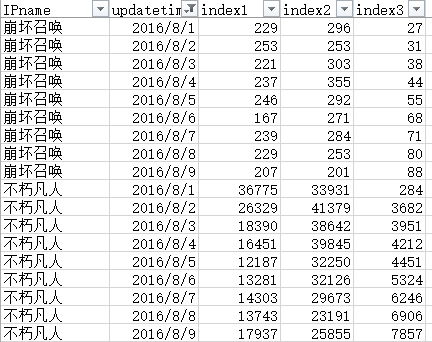
2、R语言操作数据格式，部分截图如下，这里以index3为因变量，index1与index2为解释变量： 

##加载相关包
install.packages("mice")##缺失值处理
install.packages("plm")
install.packages("MSBVAR")
library(plm)
library(MSBVAR)
library(tseries)
library(xts)
library(mice)
data<-read.csv("F://分类别//rankdata.csv",header=T,as.is=T)##读取数据

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

2、单位根检验：数据平稳性 
为避免伪回归，确保结果的有效性，需对数据进行平稳性判断。何为平稳，一般认为时间序列提出时间趋势和不变均值（截距）后，剩余序列为白噪声序列即零均值、同方差。常用的单位根检验的办法有LLC检验和不同单位根的Fisher-ADF检验，若两种检验均拒绝存在单位根的原假设则认为序列为平稳的，反之不平稳（对于水平序列，若非平稳，则对序列进行一阶差分，再进行后续检验，若仍存在单位根，则继续进行高阶差分，直至平稳，I(0)即为零阶单整，I(N)为N阶单整）。

##单位根检验
tlist1<-xts(data$index1,as.Date(data$updatetime))
adf.test(tlist1)
tlist2<-xts(data$index2,as.Date(data$updatetime))
adf.test(tlist2)

• 1
• 2
• 3
• 4
• 5

3、协整检验/模型修正 
单位根检验之后，变量间是同阶单整，可进行协整检验，协整检验是用来考察变量间的长期均衡关系的方法。若通过协整检验，则说明变量间存在长期稳定的均衡关系，方程回归残差是平稳的，可进行回归。 
格兰杰因果检验：前提是变量间同阶协整，通过条件概率用以判断变量间因果关系。

##格兰杰因果检验
granger.test(tsdata,p=2)

• 1
• 2

4、模型选择 
面板数据模型的基本形式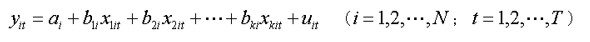 
 
也可写成：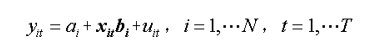 
 
其中： 
 
 

对于平衡的面板数据，即在每一个截面单元上具有相同个数的观测值，模型样本观测数据的总数等于NT。 
当N=1且T很大时，就是所熟悉的时间序列数据；当T=1而N很大时，就只有截面数据。

• 模型选择一般有三种形式 
  (1)无个体影响的不变系数模型（混合估计模型）：ai=aj=a，bi=bj=b 
   
  即模型在横截面上无个体影响、无结构变化，可将模型简单地视为是横截面数据堆积的模型。这种模型与一般的回归模型无本质区别，只要随机扰动项服从经典基本假设条件，就可以采用OLS法进行估计（共有k+1个参数需要估计），该模型也被称为联合回归模型(pooled regression model)。 
  (2)变截距模型（固定效用模型）：ai≠aj，bi=bj=b 
   
  即模型在横截面上存在个体影响，不存在结构性的变化，即解释变量的结构参数在不同横截面上是相同的，不同的只是截距项，个体影响可以用截距项ai (i＝1，2，…，N)的差别来说明，故通常把它称为变截距模型。 
  (3)变系数模型（随机效应模型）：ai≠aj，bi≠bj 
   
  即模型在横截面上存在个体影响，又存在结构变化，即在允许个体影响由变化的截距项ai (i＝1，2，…，N)来说明的同时还允许系数向量bi (i＝1，2，…，N)依个体成员的不同而变化，用以说明个体成员之间的结构变化。我们称该模型为变系数模型。
• 选择合适的面板模型 
  需要检验被解释变量yit的参数ai和bi是否对所有个体样本点和时间都是常数，即检验样本数据究竟属于上述3种情况的哪一种面板数据模型形式，从而避免模型设定的偏差，改进参数估计的有效性。 
   
  如果接受假设H2，则可以认为样本数据符合不变截距、不变系数模型。如果拒绝假设H2，则需检验假设H1。如果接受H1，则认为样本数据符合变截距、不变系数模型；反之，则认为样本数据符合变系数模型。
• F检验 
  具体计算过程略，见参考ppt。 
   
   
  其中下标1，s1指代随机效应模型的残差平方和，s2指代固定效用模型残差平方和，s3指代混合估计模型的残差平方和； 
  若F2统计量的值小于给定显著水平下的相应临界值，即F2小于Fa，则接受H2，认为样本数据符合混合效应模型；反之，则继续检验假设H1； 
  若F1统计量的值小于给定显著水平下的相应临界值，即F1小于Fa，则接受H1，认为样本数据符合固定效应模型；反之，则认为样本数据符合随机效应模型；
• 随机效应模型 
  (1)1.LM检验。Breush和Pagan于1980年提出R 检验方法。 
  其检验原假设和备择假设： 
   
  如果不否定原假设，就意味着没有随机效应，应当采用固定效应模型。 
  (2). 豪斯曼（Hausman）检验。William H Greene于1997年提出了一种检验方法，称为豪斯曼（Hausman）检验。 
  
  若统计量大于给定显著水平下临界值，p值小于给定显著水平，则存在个体固定效应，应建立个体固定效应模型。

form<- index3~index1+ index2
rankData<-plm.data(data,index=c("IPname","updatetime"))#转化为面板数据
pool <- plm(form,data=rankData,model="pooling")#混合模型
pooltest(form,data=rankData,effect="individual",model="within")#检验个体间是否有差异
pooltest(form,data=rankData,effect="time",model="within")#检验不同时间是否有差异
wi<-plm(form,data=rankData,effect="twoways",model="within")#存在两种效应的固定效应模型
pooltest(pool,wi)#F检验判断混合模型与固定效应模型比较
phtest(form,data=rankData)##Hausman检验判断应该采用何种模型,随机效应模型检验
pbgtest(form,data=rankData,model="within")#LM检验,随机效应模型检验
#检验是否存在序列相关
pwartest(form,data=rankData)#Wooldridge检验(自相关)小于0.05存在序列相关
summary(wi)##查看拟合模型信息
fixef(wi,effect="time")#不同时间对因变量的影响程度的系数估计值
inter<-fixef(wi,effect="individual")#不同个体对因变量的影响程度的截距估计值

##根据模型参数，进行预测；

百度文库中下载的参考ppt： 
http://pan.baidu.com/s/1qXHVGde

注：有些地方，尤其R代码部分有些乱，需根据实际数据情况进行选择，函数的参数设置并未完全吃透，还需要继续学习，如有不对的地方，再改正，目前的理解是这样了，在本次数据场景中，实际数据应用中预测效果不是很好，误差稍大，这次未采用，以后遇到可以再尝试。