Functional mechanism: regression analysis under differential privacy
论文学习报告
组员：裴建新 赖妍菱 周子玉
2020-03-10
1 背景
当今社会，互联网技术正日益深入人们的生活.随着网络和信息化产业的迅猛发展，数据以前所未有的速度不断地增长和累积，大数据已经成为学术界和产业界的热点，同时改变着人们的日常生活.在大数据背景下，数据量相对以往有了质的飞跃.同时，人们对信息处理的速度、信息来源的多样性信息处理的价值也有了更高的要求.然而，随着从大数据中挖掘出各种各样的敏感信息，数据参与者的隐私受到了严重威胁，这迫使人们加强对数据的隐私保护.
虽然学术界并没有通用的隐私概念，但一般意义下，通常将用户认为自身敏感且不愿公开的部分信息称为隐私.然而，如果直接将这部分信息屏蔽，数据的价值就会大打折扣.可以说，在完善地保护敏感信息的同时，有效地释放对公众有益的信息，这本身就是矛盾的事.在社会学方面，可以制定保护个人信息的法律，对恶意窥探他人隐私的行为进行惩罚，但是这种方法实施起来需要大量的人力资源，效果也不甚理想.因此，从技术上解决这个问题变得更加实际，通常的做法是通过“去识别”的方式使部分数据匿名.但不幸的是，随着数据量的增长，数据之间的关联度日益增强，一些经过“去识别”处理的匿名数据，仍然能够通过互相之间的联系得到辨认，使得预防用户身份再识别的难度与日俱增.[2]
2 研究现状
2006年，Dwork et al.提出ϵ-差分隐私的概念，表明它可以使用拉普拉斯执行机制，支持任何查询的输出是实数.这种机制在现有的工作中被广泛采用，但大多数采用仅限于聚合查询或可简化为简单聚合的查询.作为拉普拉斯机制的补充，McSherry和Talwar提出了指数机制，它适用于任何输出空间是离散的查询.这为输出不是实数的各种有趣问题提供了不同的私有解决方案.然而，无论是拉普拉斯机制还是指数机制都很难被用于回归分析.因为这两种机制都需要对目标问题进行仔细的敏感性分析.当输入数据中的任意元组被修改时，问题输出会发生很大变化.然而，由于回归输入和输出之间的复杂相关性，这样的分析对于回归任务来说相当困难.
论文中指出，目前仅有的针对回归分析的工作是由Chaudhuri等人、Smith和Lei完成的.具体来说，Chaudhuri等表明，当回归任务的代价函数是凸的、双可微的时，可以使用基于目标扰动的差分私有算法进行回归.但该算法不适用于标准的logistic回归，因为logistic回归的成本函数不满足凸性要求.相反，Chaudhuri等人证明了他们的算法可以使用修改后的输入来处理非标准类型的逻辑回归.然而，修正的逻辑回归在实践中是否有用还不清楚.Smith提出了一个统计分析的通用框架，它利用了拉普拉斯机制和指数机制.然而，该框架要求统计分析的输出空间是有限的，这使得它不适用于线性回归和逻辑回归.例如，如果我们在一个三维数据集上预形成一个线性回归，那么输出将是两个实数，两者都有一个无界域.
Lei提出了一种回归方法，避免直接对回归输出进行敏感性分析.简而言之，该方法首先使用拉普拉斯机制产生输入数据的一个有噪声的多维直方图.然后，它生成一个合成数据集，该数据集与有噪声的直方图中的统计数据相匹配，而不需要查看原始数据集.最后利用综合数据计算回归结果.但由于多维直方图只包括计数，这使它更容易执行ϵ—差分隐私，可处理拉普拉斯机制差分隐私的方式.然而，正如论文的实验对比可以观察到，Lei的方法被限制在小维度的数据集上.这是因为当输入数据的维数增加时，这种方法会产生粒度更粗的有噪直方图，从而导致合成数据和回归结果不准确.总之，现有的解决方案没有一个能产生令人满意的线性或逻辑回归结果.
3 前序知识
3.1 线性回归
线性回归[3]是回归问题中的一种.线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程.通过构建损失函数，来求解损失函数最小时的参数w和b.通常可以表示如图3.1：
图3.1 线性回归的一般表示
其中y^为预测值，自变量x和因变量y是已知的，而我们想实现的是预测新增一个x，其对应的y是多少.因此，为了构建这个函数关系，目标是通过已知数据点，求解线性模型中w和b两个参数.
求解最佳参数，需要一个标准来对结果进行衡量，为此我们需要定量化一个目标函数式，使得计算机可以在求解过程中不断地优化.
针对任何模型求解问题，都是最终都是可以得到一组预测值y^ ，对比已有的真实值y，数据行数为n，可以将损失函数定义为如图3.2(a)所示，即预测值与真实值之间的平均的平方距离，统计中一般称其为MAE(mean square error)均方误差.把图1的函数式代入损失函数，并且将需要求解的参数w和b看做是函数L的自变量（图3.2(b)）.
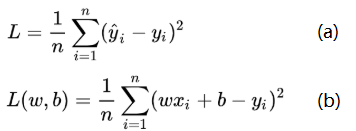
图3.2 线性回归中的函数分析
此时，线性回归的任务便是求解最小化L时w和b的值，即核心目标优化式（图3.3）.
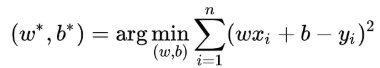
图3.3 线性回归中的核心目标优化式
3.2 逻辑回归
逻辑回归[4]虽然名字中有回归，但模型最初是为了解决二分类问题.
对线性模型进行分类如二分类任务，简单的是通过阶跃函数，即将线性模型的输出值套上一个函数进行分割，大于z的判定为0，小于z的判定为1，如图3.4(a).但这样的分段函数数学性质不好，既不连续也不可微.因此提出了Sigmoid函数，如图3.4(b).
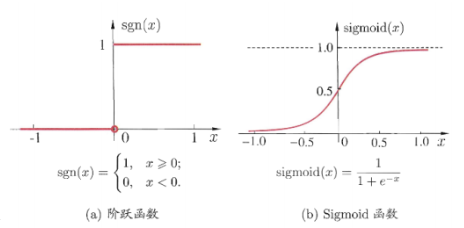
图3.4 典型的两种激活函数
回归问题的损失函数一般为平均误差平方损失MSE，逻辑回归解决二分类问题中，损失函数如图3.5(a)所示.这个函数通常称为对数损失，这里的对数底为自然对数e，其中真实值y是有0或1两种情况，而推测值y^由于借助对数几率函数，其输出是介于0~1之间连续概率值.因此损失函数可以转换为分段函数如图3.5(b)所示.
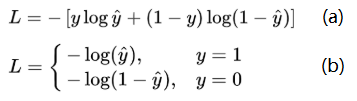
图3.5 逻辑回归中的函数分析
此时，逻辑回归的学习任务便是求解最小化L时w和b的值，即核心目标优化式（图3.6）.
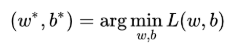
图3.6 逻辑回归中的核心目标优化式
3.3 ϵ-差分隐私
一个随机算法满足ϵ-差分隐私，敌我识别的任何输出O和任意两个邻居数据库D1和D2需要满足下述条件（见图3.7）.其中，ϵ越小，隐私保密度越高；ϵ越大，数据可用性越高；ϵ趋近于0时，两个算法的输出无限逼近.
图3.7 随机算法A满足ϵ-差分隐私的条件
3.3.1 拉普拉斯机制
（1）拉普拉斯机制的敏感度：给定一个函数集Q，D1和D2为邻近数据集，其敏感度定义如图3.8所示.
图3.8 拉普拉斯机制下的敏感度
（2）对于期望为0，方差为2b2的拉普拉斯分布，其概率密度函数如图3.9所示.
图3.9 期望为0，方差为2b2拉普拉斯机制的概率密度函数
4 核心算法
4.1 主要思想
简单来说，论文中函数机制（Functional Mechanism，FM）算法是拉普拉斯机制的一个扩展.该算法的主要特点在于：1）不直接向回归分析的结果注入噪音；2）通过干扰回归分析的优化目标函数来保证隐私.在回归分析中，我们可以通过最优化目标函数解出目标函数的最优解w*，但是如果直接发布w*会泄露隐私，为了解决这个问题，文中提出了使用拉普拉斯机制向ω֗添加噪声的方法，以此来保护数据隐私.考虑到数据集D和w之间的复杂关系，使得这个方法颇具挑战性.
与直接给w加入噪声不同，FM是直接向目标函数
添加噪声，得到一个扰动目标函数
，用扰动目标函数代替原始目标函数，通过对扰动目标函数求解得到
.而论文的难点在于如何保证添加噪声后的目标函数依然满足差分隐私的要求.
4.2 算法流程
这里我们用w作为一个含有d个元素的向量，即
.用
来表示
的乘积，其中
属于自然数集合N.用
表示所有
的乘积，有如下表达：
根据Stone-Weierstrass定理任何一个连续可微的函数都可以写成多项式的形式，因此
可以写成如下形式：
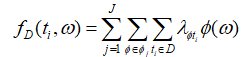
其中
，是
的系数，
.
我们通过对上述目标函数用拉普拉斯机制添加噪声可以得到一个扰动目标函数，即：
算法的主要流程如表1所示：
表1 算法流程
算法首先计算出∆这个参数，然后通过两个for循环，分别用拉普拉斯机制对
添加噪声，得到扰动目标函数的，然后就可以得到扰动目标函数，最后求出
.整个算法流程的核心就在于第四行代码，第四行代码通过拉普拉斯添加噪音，从而实现了对目标函数的扰动.
4.3 推导证明
因为整个算法是基于查分隐私的回归分析，所以要求该算法必须满足查分隐私的条件.在证明算法满足差分隐私之前，还要先证明定理1（Lemma1）.
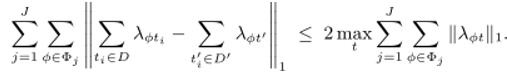
其中
表示任意一个元组.
为了不失一般性，文中假设D和D’两个邻近数据集中只有最后一个元素不一样，用
表示最后一个元组.
原始目标函数和扰动目标函数相减，可得下式：
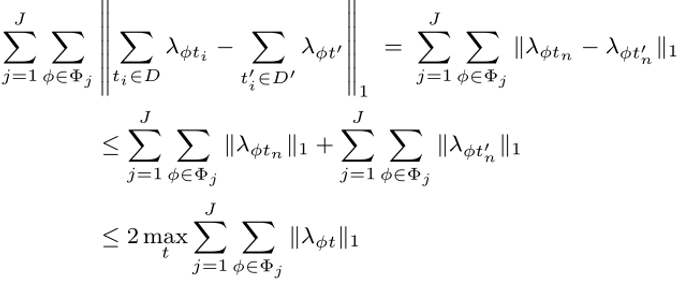
其中，第一个不等号成立的原因在于两个数之差的绝对值一定小于等于两个数绝对值之和，第二个不等号成立的原因在于两个数绝对值之和一定小于等于其中较大绝对值的二倍.
有了以上不等式，我们可以证明FM算法是满足差分隐私条件的.同样用D和D1代表两个邻近数据集，为了不失一般性，假设两个数据集中只有最后一个元组不同，根据前面提到的查分隐私的公式有：
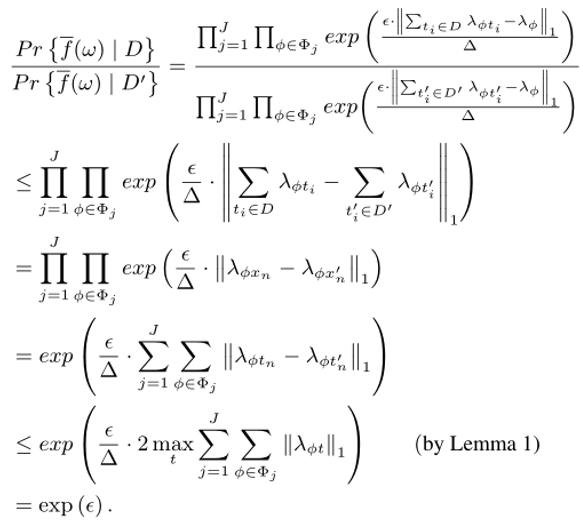
综上所述，FM算法是满足差分隐私条件的.
5 实验及算法效果
论文中针对四种方法，即DPME、过滤器优先级（FP）、NoPrivacy和截断方法，对FM的性能进行了实验评估.
实验使用了两个开源数据集，美国和巴西人口普查记录数据集，分别包含在美国和巴西收集的370，000和190，000人口普查记录.每个数据集中有13个属性，分别是年龄、性别、婚姻状况、教育程度、残疾程度、出生率、每周工作时间、当前位置的居住年数、房屋所有权、家庭规模、孩子数、汽车数量和年收入. 在这些属性中，婚姻状况是唯一的，其域包含两个以上的值的类别属性，即，单身，已婚和离婚/丧偶.按照回归分析中的常规做法，婚姻状况被转换为两个二元属性，即“单身”和“已婚”，一个离婚/丧偶的人在这两个属性上的分类值均为false.通过这种转换，我们两个数据集都变为14维.
然后对每个数据集进行回归分析，以使用剩余属性预测年收入值. 对于逻辑回归，将年收入转换为二进制属性：高于预定义阈值的值映射为1，否则为0.实验通过均方误差、误分类率、计算时间（秒）三个指标进行效果评估.
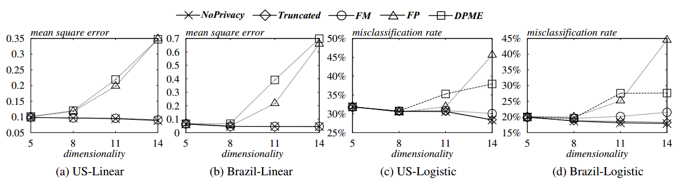
图5.1 数据集维度对均方误差、误报率的影响
从图5.1可以看出，FM始终优于FP和DPME，并且回归准确性几乎和NoPrivacy相同.从c和d得出，在数据集维数较高时，FP和DPME的误报率非常高.
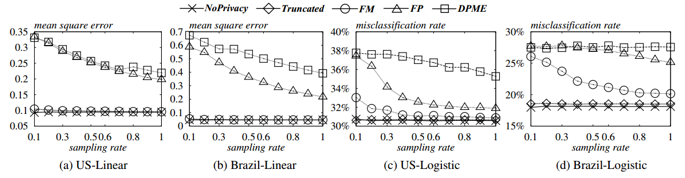
图5.2 数据集基数对均方误差、误报率的影响
从图5.2可以看出，对于这两个回归任务和两个数据集，FM的性能均显着优于FP和DPME.此外，对于线性回归，FM和NoPrivacy之间的准确性差异可以忽略不计.同时，它们的准确性在数据库中记录数变化时基本保持稳定.
图5.3 差分隐私参数对均方误差、误报率的影响
从图5.3可以看出，FM的性能均优于FP和DPME，从c和d可以看出，FP和DPME产生的回归结果准确性要差得多，尤其是当ϵ较小时.
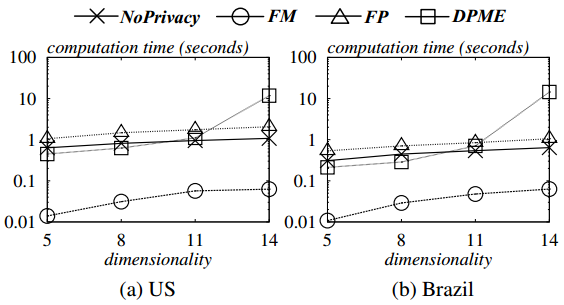
图5.4 数据集维度对计算时间的影响
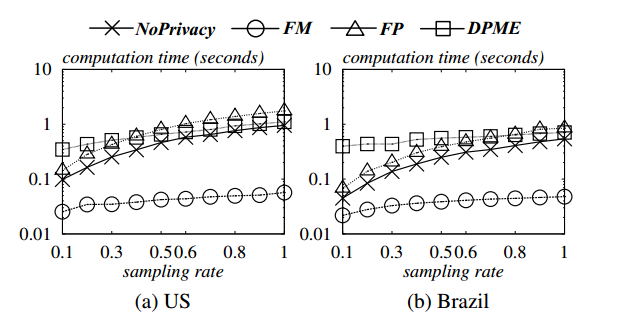
图5.5 采样率对计算时间的影响
从图5.4和图5.5可以看出，所有算法的计算时间都随数据集的维数和基数的增加而增加.但是FM的计算时间明显小于所有其他算法，效率最高.
图5.6 差分隐私参数对计算时间的影响
的变小而略有缩短，但其他算法的改变结果则不明显.综上所述，在所有实验中，FM均能得到较小的均方误差、较低的误报率以及较短的计算时间，所以FM在准确性和效率上均优于FP和DPME，这也是这篇论文的优势和创新点.
6 总结
这篇论文表明，FM是进行差分隐私回归分析的首选方法,是拉普拉斯机制的扩展，它不直接向回归结果中注入噪声，而是通过干扰回归分析的优化目标来保证隐私。论文先从理论上用大量数学公式进行推导，并且将推导的结果在实例数据集上进行了验证，得出了该算法的有效性，这给了我们启发.在看论文的过程中，我们认真对每个公式进行了理解和推导，公式的理解是这篇论文的难点，但我们齐心协力，集合大家的智慧将公式弄懂了，进而去理解整篇论文，在这个过程中，我们收获颇丰.
7 参考文献
[1] Zhang, Jun, et al. "Functional mechanism: regression analysis under differential privacy." arXiv preprint arXiv:1208.0219 (2012).
[2] 曹永知.概率系统差分隐私研究综述[J].广州大学学报(自然科学版),2019,18(04):75-82.
[3] EO_Admin.机器学习| 算法笔记- 线性回归[EB/OL]. https://www.cnblogs.com/geo-will/p/10468253.html,2019-03-10.
[4] EO_Admin.机器学习| 算法笔记- 逻辑斯蒂回归[EB/OL]. https://www.cnblogs.com/geo-will/p/10468356.html ,2019-03-10.
