基于桶的排序之基数排序以及排序方法总结

基于桶的排序之基数排序以及排序方法总结

作者：Grey

原文地址：

博客园：基于桶的排序之基数排序以及排序方法总结

CSDN：基于桶的排序之基数排序以及排序方法总结

说明

基于桶的排序有两种，分别是计数排序和基数排序。

但是这两种排序应用范围有限，需要样本的数据状况满足桶的划分

计数排序算法说明见：基于桶的排序之计数排序

基数排序

一般来讲，基数排序要求，样本是 10 进制的正整数, 流程如下

第一步：找到最大值，这个最大值是几位的，其他数不足这个位数的，用 0 补齐；

例如：

原始数组为

arr = {17,210,3065,40,71,2}

最大值为 3065，是四位的，其他都不是四位的，前面用 0 补充，所以先让数组变成

arr = {0017,0210,3065,0040,0071,0002}

第二步：准备 10 个桶，每个桶是队列；

第三步：从个位依次进桶（和对应桶中的元素用队列相连），然后依次倒出；然后根据十位数进桶（和对应桶中的元素用队列相连），依次倒出；以此类推，一直到最高进桶，然后倒出。最后倒出的顺序就是排序后的结果。

以上述数组为例，基数排序的整个流程如下

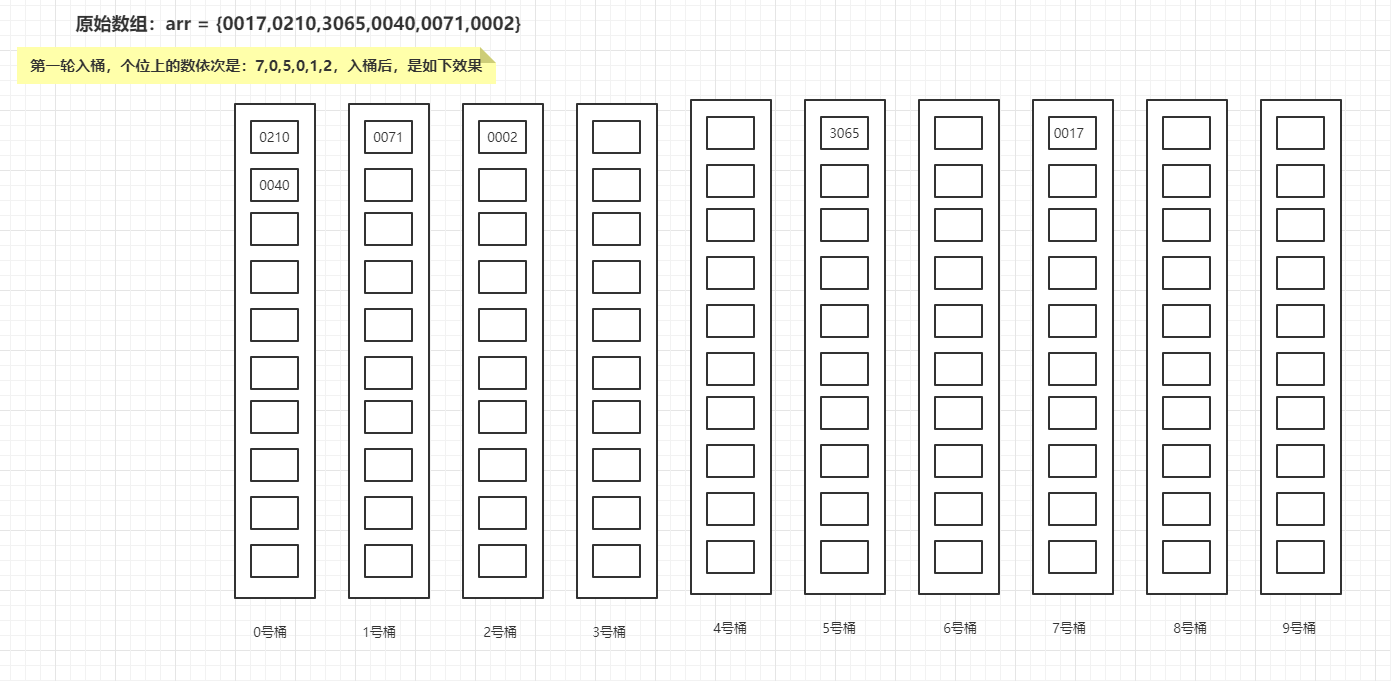
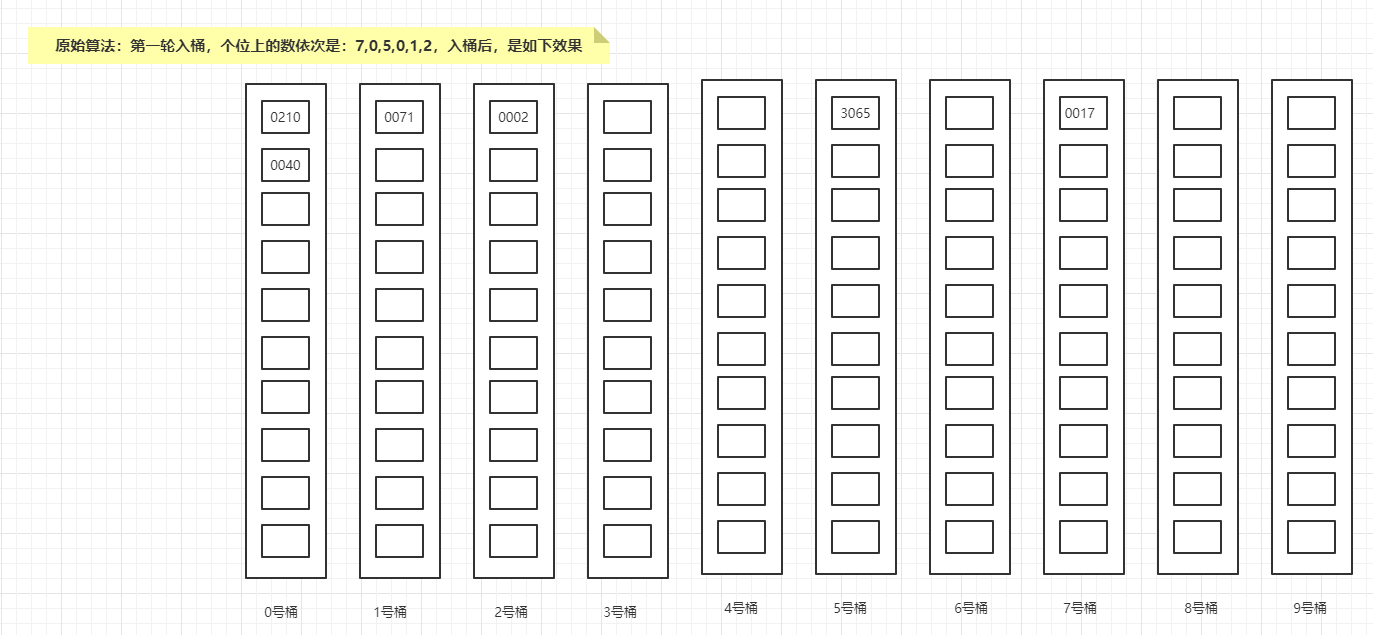
第一轮入桶，个位上的数依次是：7,0,5,0,1,2，入桶后，是如下效果:

然后出桶，第一轮结果是{0210,0040,0071,0002,3065,0017};

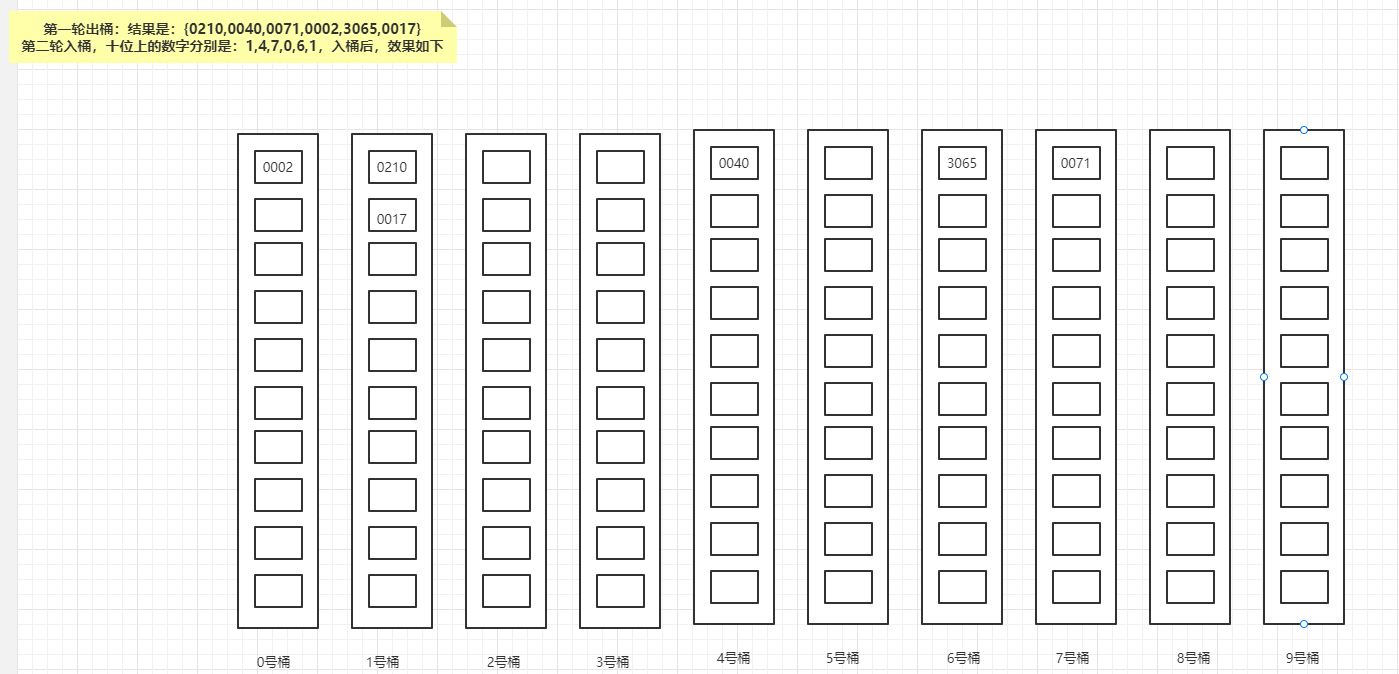
第二轮入桶，十位上的数字分别是：1,4,7,0,6,1，入桶后，效果如下:

第二轮出桶：结果是{0002,0210,0017,0040,3065,0071};

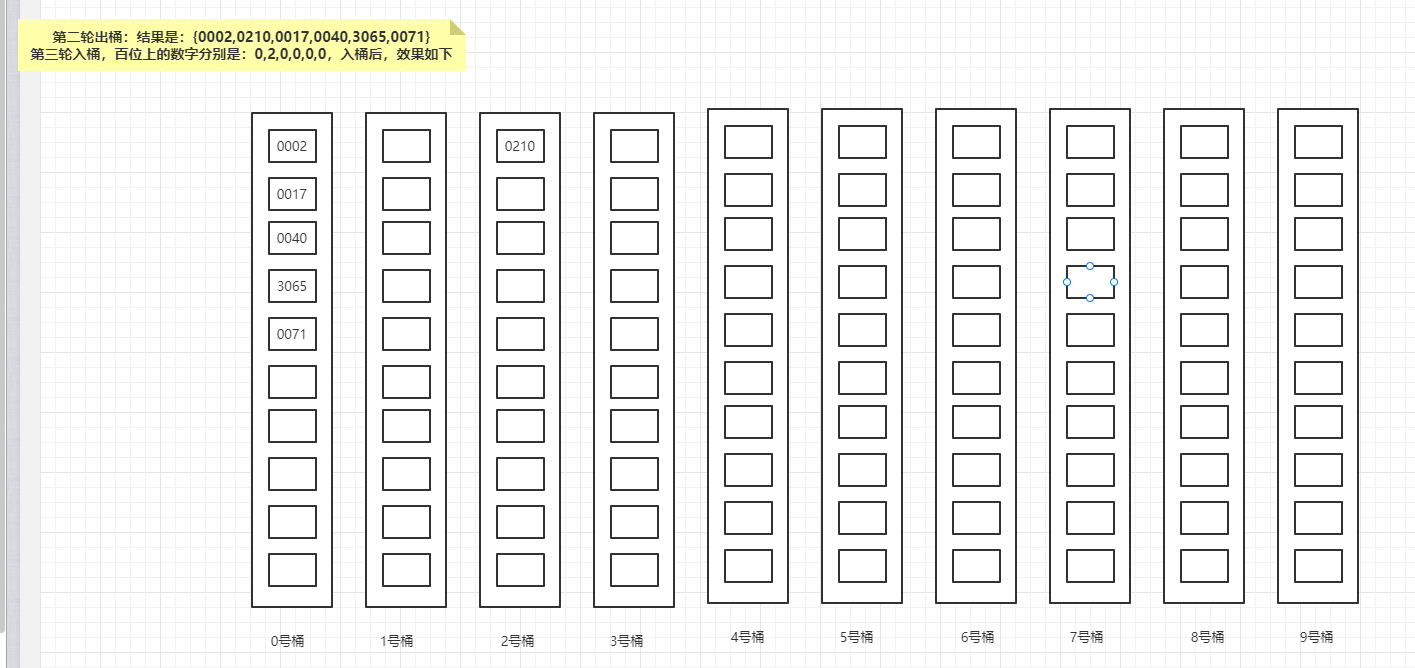
第三轮入桶，百位上的数字分别是：0,2,0,0,0,0，入桶后，效果如下:

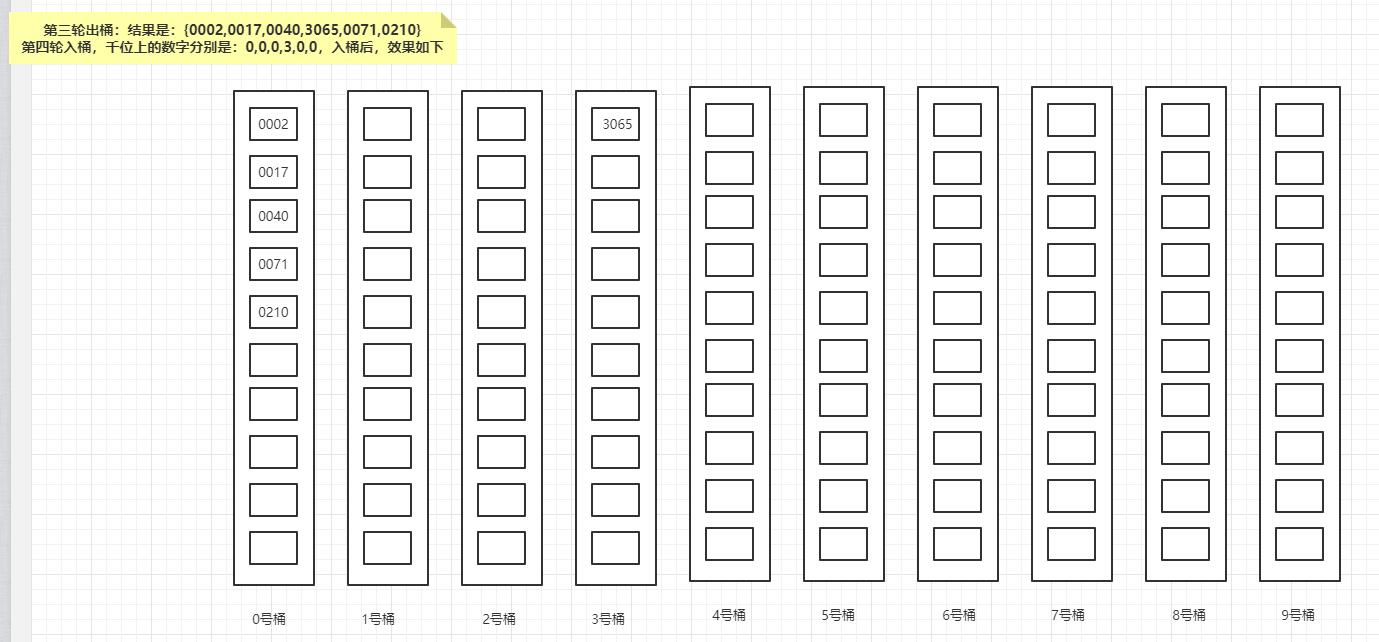
第四轮入桶，也是最后一轮入桶，千位上的数字分别是：0,0,0,3,0,0，入桶后，效果如下：

最后一轮出桶：结果是{0002,0017,0040,0071,0210,3065}，已排好序。

上述是基数排序的流程，但是在算法实现上，有更优化的解法

根据整个基数排序的算法，代码上做了一些优化，用了一个包含十个元素的数组count来表示桶，而且整个代码没有用队列这个数据结构，仅用 count 数组就实现了入桶和出桶的过程，接下来一一分析一下代码，其中helper数组用于存排序后的数组，bits表示最大数十进制一共有几位，流程和之前提到的算法流程一致：

// 从个位开始，一直到最高位，不断入桶出桶
for (int bit = 1; bit <= bits; bit++) {
    // 入桶
    // 出桶
}

入桶的逻辑，原先我们需要把入桶的值记录到桶对应的队列中，如今不需要，我们只需要记录一个个数即可，就是如下逻辑

// 从个位开始，一直到最高位，不断入桶出桶
for (int bit = 1; bit <= bits; bit++) {
    int[] count = new int[10];
    for (int num : arr) {
        count[digit(num, bit)]++;
    }
    // 出桶
}

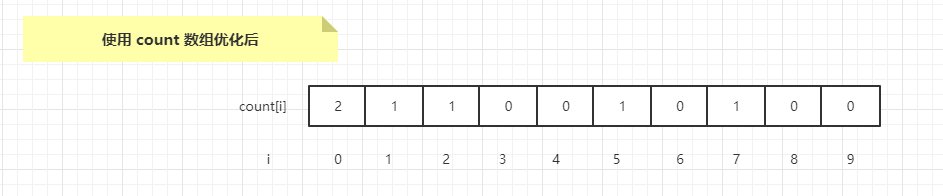
以上述示例数组来说明，示例数组初始状态是{0017,0210,3065,0040,0071,0002}，经过第一轮个位数的入桶操作，count数组会变成{2,1,1,0,0,1,0,1,0,0}，如下示例图

原始算法

用 count 优化后

可以看到 count 只存了数组中的数的有相同位数值的数有多少个。

比如：

count[0] = 2; // 说明 0 号桶在第一轮入桶的时候，有两个数，也说明个位上是 0 的数有两个。
count[5] = 1; // 说明 5 号桶在第一轮入桶的时候，有一个数，也说明个位上是 5 的数有一个。
......

接下来是出桶操作，原始算法中，值存在队列，从左到右遍历桶，桶中元素按队列遍历出来即可；优化后，只有一个count数组，count 数组只记录了个数，如何实现出桶呢？ 客观上，在第一轮中，出桶顺序是{0210,0040,0071,0002,3065,0017}，其实，就是出桶编号从小到大，桶中的数依次出来。

基于第一轮的count={2,1,1,0,0,1,0,1,0,0}可得到其前缀和数组{2,3,4,4,4,5,5,6,6,6}，最大编号且包含数组元素的桶是 7 号桶，且 7 号桶中只有一个数，就是 0017 ，所以这个数一定是最后出桶的那个数！接下来包含元素的最大桶编号是 5 号桶，5 号桶只有一个数，就是 3065，这个数一定是倒数第二顺序出来的数！依次类推，就可以把所有第一轮出桶的数按顺序提取出来，核心代码入下：

      // 前缀和
      for (int j = 1; j < 10; j++) {
        count[j] = count[j - 1] + count[j];
      }
      // 倒序遍历数组
      for (int i = arr.length - 1; i >= 0; i--) {
        int pos = digit(arr[i], bit);
        // 数组中某一位是 pos 的数，在某一轮入桶后
        // 出桶的时候，应该处在什么位置！！！
        help[--count[pos]] = arr[i];
      }

完整代码见

public class Code_RadixSort {

  // 非负数
  public static void radixSort(int[] arr) {
    if (arr == null || arr.length <= 1) {
      return;
    }
    int max = arr[0];
    for (int i = 1; i < arr.length; i++) {
      max = Math.max(arr[i], max);
    }
    // 最大值有几位
    int bits = 0;
    while (max != 0) {
      bits++;
      max /= 10;
    }
    int[] help = new int[arr.length];
    for (int bit = 1; bit <= bits; bit++) {
      int[] count = new int[10];
      for (int num : arr) {
        count[digit(num, bit)]++;
      }
      // 前缀和
      for (int j = 1; j < 10; j++) {
        count[j] = count[j - 1] + count[j];
      }
      // 倒序遍历数组
      for (int i = arr.length - 1; i >= 0; i--) {
        int pos = digit(arr[i], bit);
        help[--count[pos]] = arr[i];
      }
      int m = 0;
      for (int num : help) {
        arr[m++] = num;
      }
    }
  }

  // 获取某个数在某一位上的值
  // 从1开始，从个位开始
  public static int digit(int num, int digit) {
    return ((num / (int) Math.pow(10, digit - 1)) % 10);
  }
}

排序总结

	时间复杂度	额外空间复杂度	稳定性
选择排序	O(N^2)	O(1)	无
冒泡排序	O(N^2)	O(1)	有
插入排序	O(N^2)	O(1)	有
归并排序	O(N*logN)	O(N)	有
随机快排	O(N*logN)	O(logN)	无
堆排序	O(N*logN)	O(1)	无
计数排序	O(N)	O(M)	有
基数排序	O(N)	O(N)	有

选择排序做不到稳定性，比如：5，5，5，5，5，3，5，5，5

冒泡排序可以做到稳定性，在相等的时候，不往右即可

插入排序可以做到稳定性，在相等的时候，不往左边继续交换即可

快排做不到稳定性，因为partition过程无法稳定，某个数会和小于等于区域交换

0）排序稳定性关键在于处理相等的时候

1）不基于比较的排序，对样本数据有严格要求，不易改写

2）基于比较的排序，只要规定好两个样本怎么比大小就可以直接复用

3）基于比较的排序，时间复杂度的极限是O(N*logN)

4）时间复杂度O(N*logN)、额外空间复杂度低于O(N)、且稳定的基于比较的排序是不存在的。

5）为了绝对的速度选快排、为了省空间选堆排、为了稳定性选归并

更多

算法和数据结构笔记

参考资料

算法和数据结构体系班-左程云