乘积小于 K 的子数组

乘积小于 K 的子数组

作者：Grey

原文地址:

博客园：乘积小于 K 的子数组

CSDN：乘积小于 K 的子数组

题目链接#

LeetCode 713. Subarray Product Less Than K

给你一个整数数组 nums 和一个整数 k ，请你返回子数组内所有元素的乘积严格小于 k 的连续子数组的数目。

示例 1：

输入 nums = [10,5,2,6], k = 100

输出：8

解释：8 个乘积小于 100 的子数组分别为：[10]、[5]、[2]、[6]、[10,5]、[5,2]、[2,6]、[5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于 100 的子数组。

示例 2：

输入：nums = [1,2,3], k = 0
输出：0

提示:

1 <= nums.length <= 3 * 10^4
1 <= nums[i] <= 1000
0 <= k <= 10^6

主要思路#

由于题目要求中说明了，数组的元素都是正数。

说明区间累乘积和区间大小有单调性，

可以使用滑动窗口解法，如果L...R区间内满足累乘积小于 k，那么必须以L开头的满足乘积小于 k 的子数组有(R - L + 1)个，

如下图：

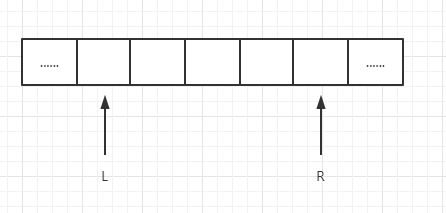
假设L = 3，R = 7，那么满足条件的子数组是：

[L...L]，

[L...L+1],

[L...L+2],

[L...L+3],

[L...L+4],

正好R - L + 1 = 5个。

接下来，继续求必须以L+1开头的满足乘积小于 k 的子数组个数。

代码见：

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        if (k <= 1) {
            return 0;
        }
        int L = 0;
        int R = 0;
        int count = 0;
        int base = 1;
        while (R < nums.length) {
            base *= nums[R];
            while (base >= k) {
                base /= nums[L++];
            }
            // L...R 满足条件
            // R + 1 是第一个不满足的位置。
            count += (R - L + 1);
            R++;
        }
        return count;
    }
}

时间复杂度O(N)，空间复杂度O(1)

更多#

算法和数据结构笔记