使用单调栈来解决的一些问题
使用单调栈来解决的一些问题
作者：Grey
原文地址：
单调栈说明
使用单调栈可以实现
数组中任意一个元素的左边和右边离它最近的比它小（大）的数，且时间复杂度\(O(N)\)
先考虑数组中无重复值的情况，题目描述见：
准备一个栈结构，栈底到栈顶从小到大，数组中的值依次入栈，入栈条件是：
-
栈为空
-
入栈的元素比栈顶元素大
当不满足上述两个入栈条件的情况下，就需要从栈顶弹出元素
弹出的时候，假设弹出的值是 A ，
那么让它弹出的值就是 A 右边离它最近的最小值，
原先 A 压的是谁，那么谁就是 A 左边离它最近的最小值。
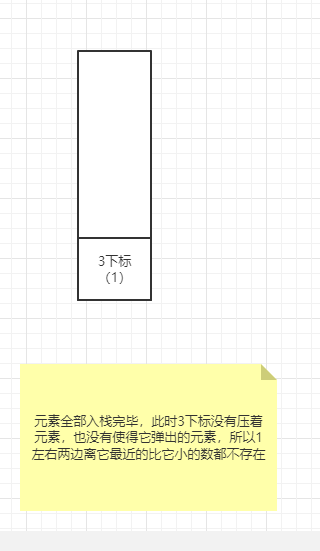
数组中的元素全部遍历完，假设栈中还有元素，则栈中元素右侧不存在离它最近的比它小的数，左侧离它最近比它小的数就是它压着的数。
注: 栈中存的是数组下标而非数组值！
示例图如下
假设数组为arr = {5,3,4,1}，
栈初始状态，0号下标直接入栈
接下来是1号下标准备入栈，因为3 < 5，所以此时栈顶的元素要出栈，由于 5 没有压着栈元素，所以 5 左边离它最近的比它小的数不存在，为-1。5 右边离它最近的比它小的数就是当前要入栈的 1 下标的 3。
接下来是 2 号下标，满足入栈条件，直接入栈。
接下来是 3 号下标的 1 准备入栈，由于1 < 4，所以此时要出栈，由于 2 下标压着 1 下标，所以 4 左边离它最近的比它小的数是 3。4 右边离它最近的比它小的数就是当前要入栈的 3 下标的 1。
弹出 2 号下标后，依然满足出栈条件，同理，栈中 1 号下标的 3 也要弹出。
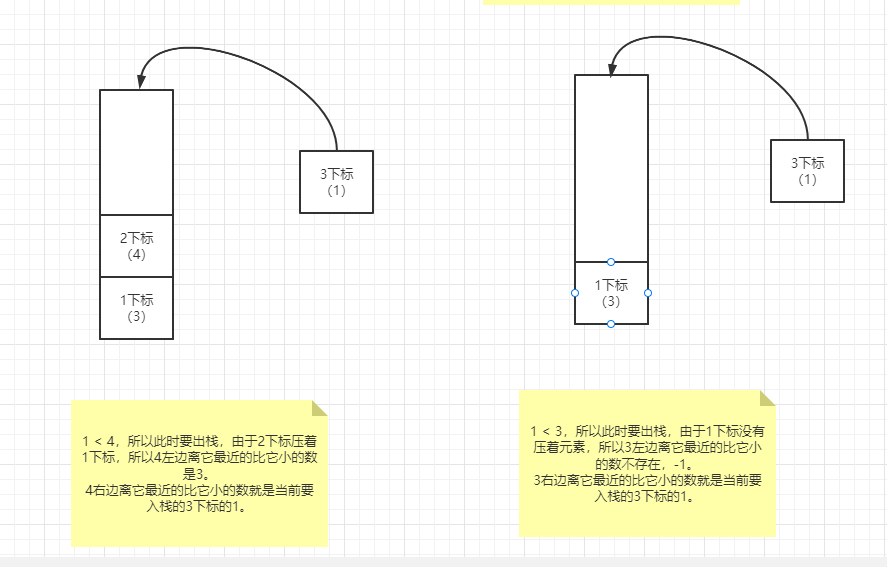
全部遍历完毕，剩下的元素依次出栈。
完整代码如下
// 注：要确保arr中无重复值！
public static int[][] getNearLessNoRepeat(int[] arr) {
int[][] res = new int[arr.length][2];
// 栈底到栈顶从小到大
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
int index = stack.pop();
res[index][0] = stack.isEmpty() ? -1 : stack.peek();
res[index][1] = i;
}
stack.push(i);
}
while (!stack.isEmpty()) {
int index = stack.pop();
res[index][1] = -1;
res[index][0] = stack.isEmpty() ? -1 : stack.peek();
}
return res;
}
在有重复值的情况下，题目描述见牛客：单调栈结构进阶(数组有重复值)
整体流程是一样的，只是在处理重复值的时候，有一些细微的差别，原先使用的是Stack<Integer>存每个位置左右侧离它最近的比它小的数，现在我们改成Stack<List<Integer>>存连续的一批重复值左右侧离它最近的比它小的数即可。在弹出栈的过程中，原先是弹出一个，然后结算，现在是弹出一批，同时结算这一批的元素。
完整代码如下
public static int[][] getNearLess(int[] arr) {
int[][] result = new int[arr.length][2];
// 重复的元素压入一批
Stack<List<Integer>> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
List<Integer> selected = stack.pop();
// 原先是结算一个，现在是结算一批
for (int popIndex : selected) {
result[popIndex][0] = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
result[popIndex][1] = i;
}
}
if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {
stack.peek().add(i);
} else {
List<Integer> list = new ArrayList<>();
list.add(i);
stack.add(list);
}
}
while (!stack.isEmpty()) {
List<Integer> list = stack.pop();
for (int popIndex : list) {
result[popIndex][0] = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
result[popIndex][1] = -1;
}
}
return result;
}
类似题目：LeetCode 739. Daily Temperatures
代码如下
class Solution {
public static int[] dailyTemperatures(int[] arr) {
if (arr == null || arr.length == 0) {
return new int[]{};
}
int n = arr.length;
int[] ans = new int[n];
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && arr[stack.peek()] < arr[i]) {
int popIndex = stack.pop();
ans[popIndex] = i - popIndex;
}
stack.push(i);
}
// 不需要弹，因为本身初始化就是0，而且栈中的元素本身就没有右边离它最近的比它大的数
return ans;
}
}
子数组累加和乘以子数组最小值所得到的结果最大是多少
题目描述见：牛客：编程题2
暴力方法的主要思路
如果我们枚举必须以数组某个位置作为最小值的情况下，如何得到最大的结果，那答案必定在其中。
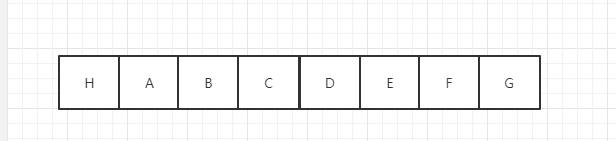
示例数组如下（为了不混淆，我用字母表示数字）
如果枚举
必须以 H 作为最小值，得到的最大结果是多少，假设结果是 HS。
必须以 A 作为最小值，得到的最大结果是多少，假设结果是 AS。
必须以 B 作为最小值，得到的最大结果是多少，假设结果是 BS。
...
必须以 G 作为最小值，得到的最大结果是多少，假设结果是 GS。
那么 HS，AS，BS ...... GS 中的最大值，就是本题的答案。
所以，本题的暴力解法是
public static int max1(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
for (int j = i; j < arr.length; j++) {
int minNum = Integer.MAX_VALUE;
int sum = 0;
for (int k = i; k <= j; k++) {
sum += arr[k];
minNum = Math.min(minNum, arr[k]);
}
max = Math.max(max, minNum * sum);
}
}
return max;
}
显然是\(O(N^3)\)的时间复杂度。
利用单调栈，本题时间复杂度可以优化为\(O(N)\)。
思路如下
首先有一个优化的点：是如何快速得到区间的和？
我们可以通过前缀和辅助数组来加速得到一个区间的和。
第二个关键点: 由于需要得到区间的最小值，所以，如果我们得到某个位置左右两侧离它最近的比它小的元素位置在哪里，就可以定位到：以这个元素为最小值的最大区间和是多少。
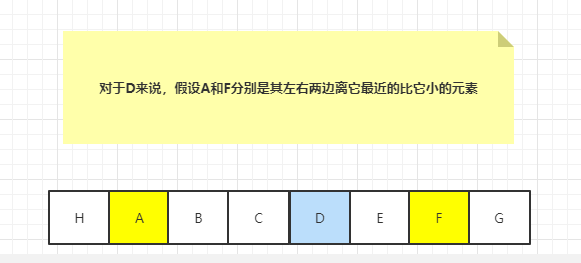
示例图如下，
对 D 这个元素来说，如果 A 和 F 是 D 左右两侧比它小的离它最近的元素，那么以 D 为最小值，可以扩散的最大区间和是 B + C + D + E 的累加和。
而这个就是单调栈可以解决的问题，完整代码如下
public static int max2(int[] arr) {
int[] sum = new int[arr.length];
sum[0] = arr[0];
// 前缀和数组优化
for (int i = 1; i < arr.length; i++) {
sum[i] = sum[i - 1] + arr[i];
}
int ans = arr[0] * arr[0];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
int popIndex = stack.pop();
// 结算
ans = Math.max(arr[popIndex] * (sum[i - 1] - (stack.isEmpty() ? 0 : sum[stack.peek()])), ans);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int popIndex = stack.pop();
ans = Math.max(arr[popIndex] * (sum[arr.length - 1] - (stack.isEmpty() ? 0 : sum[stack.peek()])), ans);
}
return ans;
}
LeetCode 有类似的题目『子数组的最小值之和』
题目描述见：LeetCode 907. Sum of Subarray Minimums
完整代码如下
class Solution {
static int MOD = (int) 1e9 + 7;
// arr[i]左右两边离i最近的比arr[i]小的位置是m，n
// 必须以arr[i]作为最小值的子数组有 (i - m) * (n - i)
public static int sumSubarrayMins(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
long max = 0;
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
Integer popIndex = stack.pop();
max += (long) arr[popIndex] * (popIndex - (stack.isEmpty() ? -1 : stack.peek())) * (i - popIndex);
}
stack.push(i);
}
while (!stack.isEmpty()) {
Integer popIndex = stack.pop();
max += (long) arr[popIndex] * (popIndex - (stack.isEmpty() ? -1 : stack.peek())) * (arr.length - popIndex);
}
return (int) (max % MOD);
}
}
直方图最大矩形的面积
题目描述见：LeetCode 84. Largest Rectangle in Histogram
这一题本质上就是枚举：
必须以arr[i]位置的值为右边界的最大矩形面积是多少。
如果得到了每个位置的这个指标，最大值就是本题的答案。
而 必须以arr[i]位置的值为右边界的最大矩形面积是多少。 其实就是在求，arr[i]左侧离它最近的比它小的元素在哪？
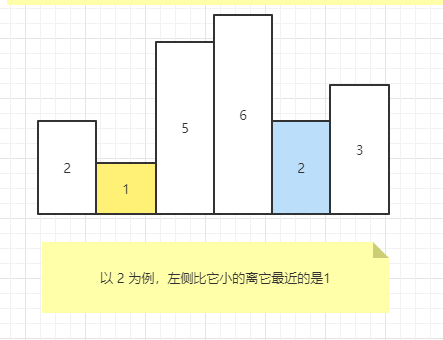
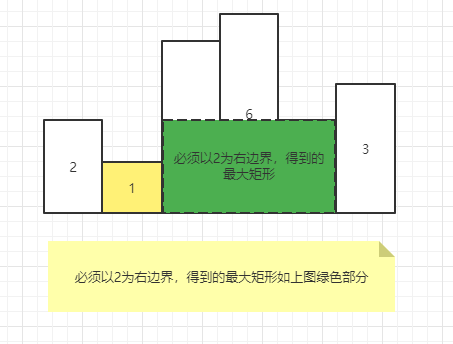
示例图
以 2 为例，左侧比它小的离它最近的是 1。那么必须以 2 位置为右边界的最大矩形如下
使用单调栈来解，代码如下
public static int largestRectangleArea(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int max = arr[0];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
int m = stack.pop();
max = Math.max(max, arr[m] * (i - (stack.isEmpty() ? -1 : stack.peek()) - 1));
}
stack.push(i);
}
while (!stack.isEmpty()) {
int popIndex = stack.pop();
max = Math.max(max, arr[popIndex] * (arr.length - (stack.isEmpty() ? -1 : stack.peek()) - 1));
}
return max;
}
有了这题做铺垫，那么 LeetCode 中『找出只包含1的最大矩形的面积』这个问题
题目链接见：LeetCode 85. Maximal Rectangle
也是同样的思路，只不过，我们需要转换一下，把二维矩阵转换成一维数组，
public static void merge(int[] help, char[] m) {
for (int i = 0; i < help.length; i++) {
help[i] = m[i] == '0' ? 0 : help[i] + 1;
}
}
完整代码如下
class Solution {
public static int maximalRectangle(char[][] m) {
int[] help = new int[m[0].length];
int max = 0;
for (int i = 0; i < m.length; i++) {
merge(help, m[i]);
max = Math.max(max, largestRectangleArea(help));
}
return max;
}
public static void merge(int[] help, char[] m) {
for (int i = 0; i < help.length; i++) {
help[i] = m[i] == '0' ? 0 : help[i] + 1;
}
}
public static int largestRectangleArea(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int max = arr[0];
int[] stack = new int[arr.length];
int index = -1;
for (int i = 0; i < arr.length; i++) {
while (index != -1 && arr[stack[index]] >= arr[i]) {
int popIndex = stack[index--];
max = Math.max(max, arr[popIndex] * (i - (index == -1 ? -1 : stack[index]) - 1));
}
stack[++index] = i;
}
while (index != -1) {
int popIndex = stack[index--];
max = Math.max(max, arr[popIndex] * (arr.length - (index == -1 ? -1 : stack[index]) - 1));
}
return max;
}
}
注：对于\(N * N\)的矩阵，内部有\(N^4\)次方个矩形，所以这题的暴力解法，时间复杂度是\(O(N^4)\)。
而采用了单调栈优化后，时间复杂度优化到了\(O(N^2)\)。
统计全 1 子矩形个数
题目链接见：LeetCode 1504. Count Submatrices With All Ones
本题的主要思路是：必须以每一行做底的全为 1 的子矩阵是多少，得到每一行的指标后，求和即可；N 为长的矩形一共包含的子矩阵有\((N*(N+1)) / 2\)
由于本题中矩阵中的值不是 0 就是 1， 所以可以借鉴『直方图最大矩形的面积』的解法
完整代码如下：
class Solution {
public int numSubmat(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
int[] help = new int[matrix[0].length];
int count = 0;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (i == 0) {
help[j] = matrix[0][j] == 1 ? 1 : 0;
} else {
help[j] += matrix[i][j] == 1 ? 1 : (-help[j]);
}
}
count += max(help);
}
return count;
}
public static int max(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int nums = 0;
// 用固定数组来替代Java自带的栈结果
int[] stack = new int[height.length];
int si = -1;
for (int i = 0; i < height.length; i++) {
// si = -1 说明栈为空
// 栈顶：height[stack[si]]
while (si != -1 && height[stack[si]] >= height[i]) {
int cur = stack[si--];
if (height[cur] > height[i]) {
int left = si == -1 ? -1 : stack[si];
int n = i - left - 1;
int down = Math.max(left == -1 ? 0 : height[left], height[i]);
nums += (height[cur] - down) * num(n);
}
}
// 入栈
stack[++si] = i;
}
while (si != -1) {
int cur = stack[si--];
int left = si == -1 ? -1 : stack[si];
int n = height.length - left - 1;
int down = left == -1 ? 0 : height[left];
nums += (height[cur] - down) * num(n);
}
return nums;
}
public static int num(int n) {
return ((n * (1 + n)) >> 1);
}
}
注：本题使用数组来替换 Java 中的是 Stack，属于常规操作，因为 Java 中的 Stack 有一些性能问题，参考：Difference between Deque and Stack
本文所有图例见：processon:使用单调栈来解决的一些问题
更多
本文来自博客园，作者：Grey Zeng，转载请注明原文链接：https://www.cnblogs.com/greyzeng/p/16654877.html
