使用二分法来解决的一些问题
使用二分法来解决的一些问题
作者:Grey
原文地址:
在一个有序数组中,找某个数是否存在#
在线测评见:LintCode 14 · 二分查找
思路:
-
由于是有序数组,可以先得到中点位置,中点可以把数组分为左右半边;
-
如果中点位置的值等于目标值,先用一个一个变量记录找到的位置,再去左侧找是否有更前的值也满足;
-
如果中点位置的值小于目标值,则去数组中点左侧按同样的方式寻找;
-
如果中点位置的值大于目标值,则取数组中点右侧按同样的方式寻找;
-
如果最后没有找到,则返回:-1。
注:本题采用了LintCode测评,如果是 LeetCode,会保证数组中的满足条件的数据至多只有一个,而LintCode中,会存在多个满足条件的数据,LintCode的要求是找到满足条件的第一个值所在的位置,所以,在LintCode这个题目的处理过程中,执行到上述第2步的时候,不能马上返回中点位置,而是继续去左侧找是否有更前的位置也满足条件。比如
nums = [1,9,9,9,1], target = 9
第一次取中点位置的时候,数组2号下标的 9 其实已经匹配到了,但是题目要求要找到数组 1 号位置的 9, 则此时就需要继续往左边找。
完整代码见
public class Solution {
public int binarySearch(int[] nums, int target) {
if (null == nums || nums.length == 0) {
return -1;
}
int result = -1;
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
// 继续去左边找
result = mid;
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
}
时间复杂度
在一个有序数组中,找大于等于某个数最左侧的位置#
在线测评见:LeetCode 35. Search Insert Position
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
说明:如果要在 num 这个数组中插入 5 这个元素,应该是插入在元素 3 和 元素 5 之间的位置,即数组的 2 号位置。
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
说明:如果要在 num 这个数组中插入 2 这个元素,应该是插入在元素 1 和 元素 3 之间的位置,即数组的 1 号位置。
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
说明:如果要在 num 这个数组中插入 7 这个元素,应该是插入在数组末尾,即 数组的 4 号位置。
通过上述示例可以知道,这题本质上就是求在一个有序数组中,找数组中元素大于等于某个数最左侧的位置,如果不存在,说明整个数组的数就没有大于目标值的,那就要把目标值插入末尾位置,即:返回数组长度。
我们只需要在二分查找这个例子上进行简单改动即可,在本问题中,因为要找到最左侧的位置,
所以,
在遇到 nums[mid] == target 的时候,不用直接返回,而是先把 mid 位置记录下来,然后继续去左侧找是否还有满足条件的更左边的位置。
同时,
在遇到nums[mid] > target条件下,也需要记录下此时的 mid 位置,因为这也可能是满足条件的位置。
代码:
class Solution {
public int searchInsert(int[] nums, int target) {
int result = nums.length;
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
result = mid;
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
result = mid;
right = mid - 1;
}
}
return result;
}
}
和二分查找一样,这个算法的时间复杂度也是
在排序数组中查找元素的第一个和最后一个位置#
OJ见:LeetCode 34. Find First and Last Position of Element in Sorted Array
思路
本题也是用二分来解,当通过二分找到某个元素的时候,不急着返回,而是继续往左(右)找,看能否找到更左(右)位置匹配的值。
代码如下:
class Solution {
public int[] searchRange(int[] nums, int target) {
return new int[]{left(nums, target), right(nums,target)};
}
public int left(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return -1;
}
int left = 0;
int right = nums.length - 1;
int result = -1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
result = mid;
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
public int right(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return -1;
}
int left = 0;
int right = nums.length - 1;
int result = -1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
result = mid;
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
}
时间复杂度
局部最大值问题#
题目描述见:LeetCode 162. Find Peak Element
思路
假设数组长度为 N ,首先判断 0 号位置的数和 N-1 号位置的数是不是峰值位置。
0 号位置只需要和 1 号位置比较,如果 0 号位置大, 0 号位置就是峰值位置,可以直接返回。
N-1 号位置只需要和 N-2 号位置比较,如果 N-1 号位置大, N-1 号位置就是峰值位置,可以直接返回。
如果 0 号位置和 N-1 在上轮比较中均是最小值,那么数组的样子必然是如下情况:
由上图可知,0 到 1 这段是增长趋势, N-2 到 N-1 这段是下降趋势。
那么峰值位置必在[1...N-2]之间出现。
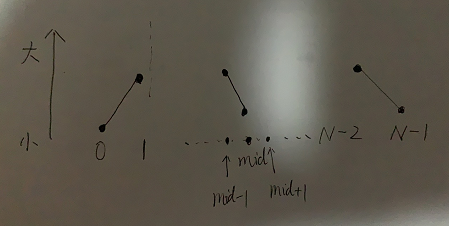
此时可以通过二分来找峰值位置,先来到中点位置,假设中点为 mid ,如果中点位置的值比左右两边的值都大,即:
arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]
则 mid 位置即峰值位置,直接返回。
否则,有如下两种情况:
情况一:mid 位置的值比 mid - 1 位置的值小
趋势如下图:
则在[1...(mid-1)]区间内继续上述二分。
情况二:mid 位置的值比 mid + 1 位置的值小
趋势是:
则在[(mid+1)...(N-2)]区间内继续上述二分。
如果最后都没找到,返回 -1 即可。
由于题目已经说明:
对于所有有效的 i 都有nums[i] != nums[i + 1]。
所以,不会有相邻相等的情况。
完整代码如下
class Solution {
public int findPeakElement(int[] nums) {
// 处理 nums <= 2 的情况
if (nums.length == 1) {
return 0;
}
if (nums.length == 2) {
return nums[0] > nums[1]?0:1;
}
int left = 0;
int right = nums.length - 1;
if (nums[left] > nums[left + 1]) {
return left;
} else {
left = left + 1;
}
if (nums[right] > nums[right - 1]) {
return right;
} else {
right = right - 1;
}
if (left == right) {
return left;
}
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
} else if (nums[mid] > nums[mid + 1]) {
right = mid - 1;
} else if (nums[mid] > nums[mid - 1]) {
left = mid + 1;
} else {
// nums[mid] < nums[mid - 1] && nums[mid] < nums[mid + 1]
left = mid + 1;
}
}
return -1;
}
}
时间复杂度
更多#
作者:GreyZeng
出处:https://www.cnblogs.com/greyzeng/p/16622554.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。
你可以在这里自定义其他内容
本文来自博客园,作者:Grey Zeng,转载请注明原文链接:https://www.cnblogs.com/greyzeng/p/16622554.html

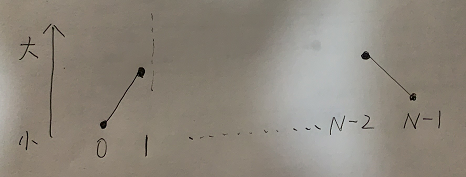



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· Qt个人项目总结 —— MySQL数据库查询与断言