接雨水系列问题

接雨水系列问题

作者：Grey

原文地址：

博客园：接雨水系列问题

CSDN：接雨水系列问题

LeetCode 42. 接雨水

主要思路：考虑每个位置，顶部可以留下多少水，累加起来，就是总的接水量。

其中，最右侧和最左侧的顶部无法接到水，因为水会从两侧流走。

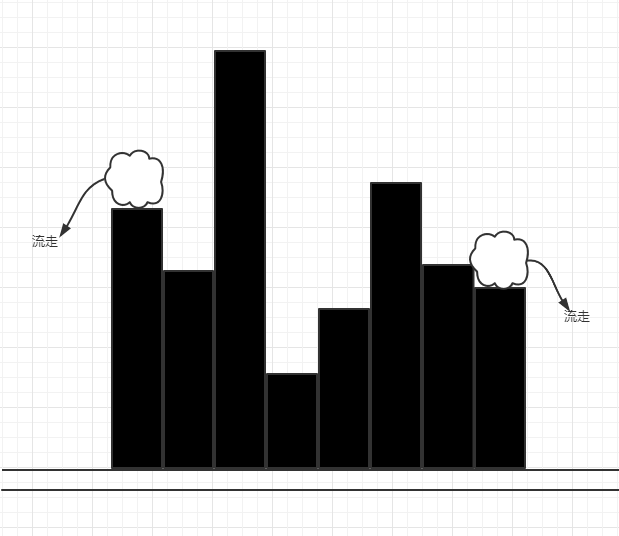
基于上述逻辑，至少可以判断，如果数组的长度小于等于2，直接返回0份水。

当数组的长度大于2，我们需要考虑，从1号位置到数组长度-2，每个位置顶部能接多少水。

设置四个变量

        int l = 1;
        int r = arr.length - 2;
        // 左侧目前高度的瓶颈是多少
        int lMax = arr[0];
        // 右侧目前高度的瓶颈是多少
        int rMax = arr[arr.length - 1];

lMax和rMax作为左侧和右侧的在当前状态下的瓶颈，我们实际遍历的位置从l到r，看下arr[l]和arr[r]位置基于左右侧的瓶颈能收集到的水量是多少。

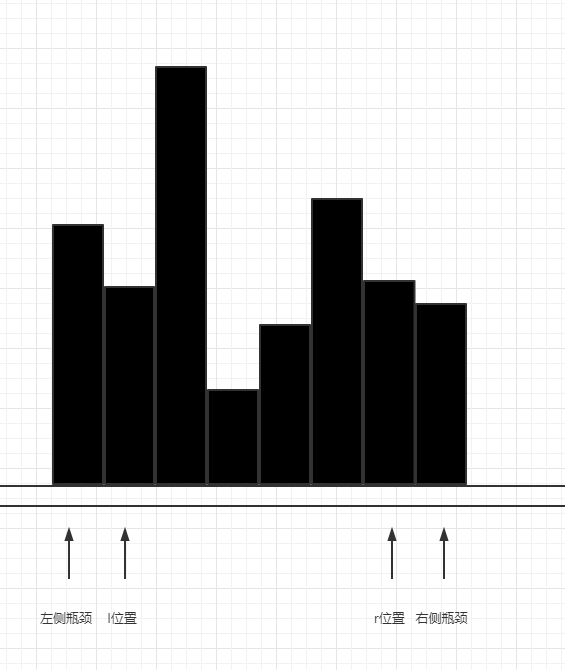
首先，虽然有两个瓶颈值，但是，我们在结算的时候，只能以较小的瓶颈值来结算，因为如果以较大瓶颈值来结算，小的瓶颈会拉低当前的结算值（木桶效应）。

所以，有两种情况：

情况一：lMax > rMax

情况二：lMax <= rMax

在情况一下，例如

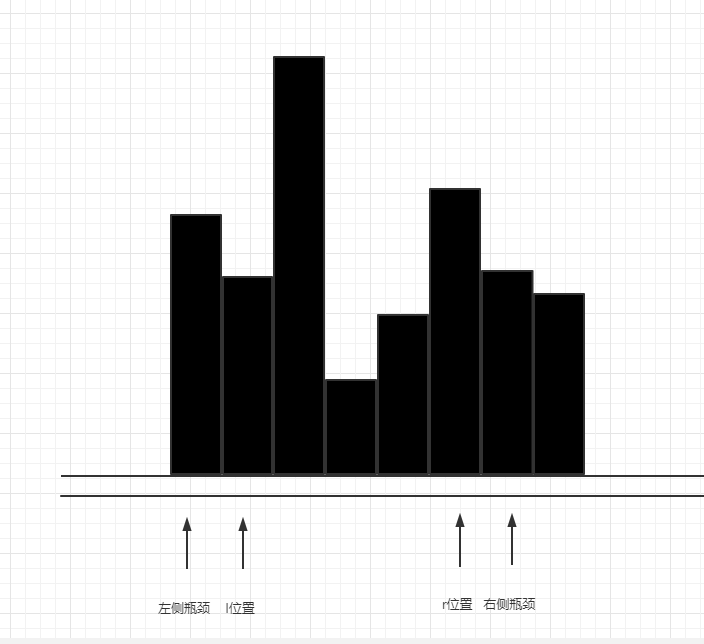
在这种情况下，我们可以确定arr[r]位置上的水能接多少，因为arr[r]和右侧瓶颈是确定的关系，左侧瓶颈虽然比arr[r]大，是水会因为右侧瓶颈让arr[r]收集的水流走，所以此时

arr[r]上可以收集的水量就是arr[r]和rMax之间的差值，如果是负数，则为0，相当于没有收到水，此时，r位置遍历完毕，右侧瓶颈更新为Math.max(arr[r],rMax)，按上图示例，现在的右侧瓶颈变成了arr[r]上的值。如下图

在这种状态下，相对小的瓶颈是rMax，又可以结算当前arr[r]位置的水量，还是0。然后继续更新右侧瓶颈，如下图

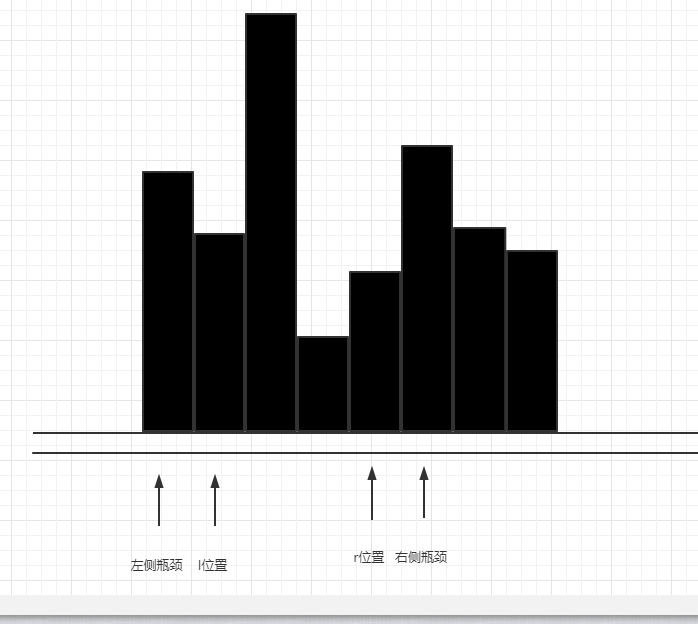
此时，左侧瓶颈是较小的那个，现在就要更新arr[l]头顶上的水量，即：arr[l]和lMax之间差值和0比较较大的那个，然后移动l指针，更新左侧瓶颈（由于arr[l]值没有lMax大，所以左侧瓶颈保留在原先lMax位置），如下图。

接下来lMax < rMax，继续结算arr[l]，移动l和更新lMax

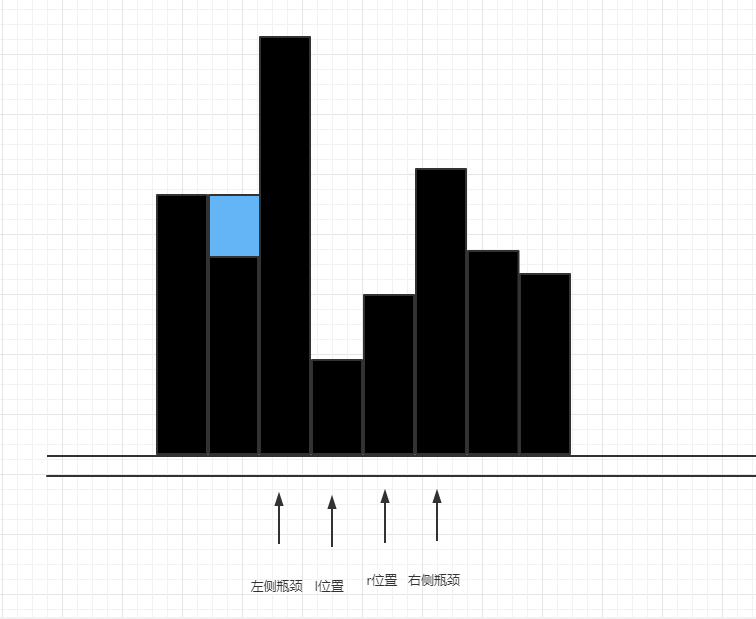
接下来的过程同理，示意图如下

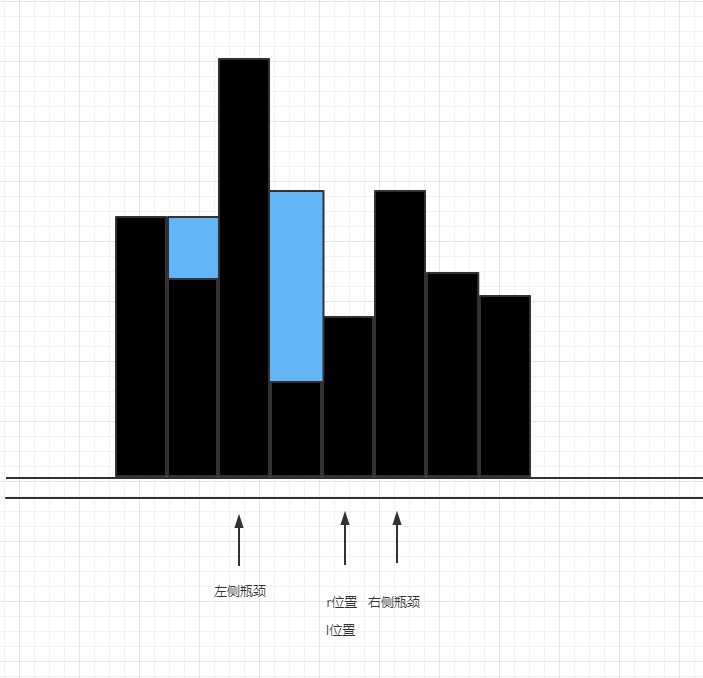
直到l>r

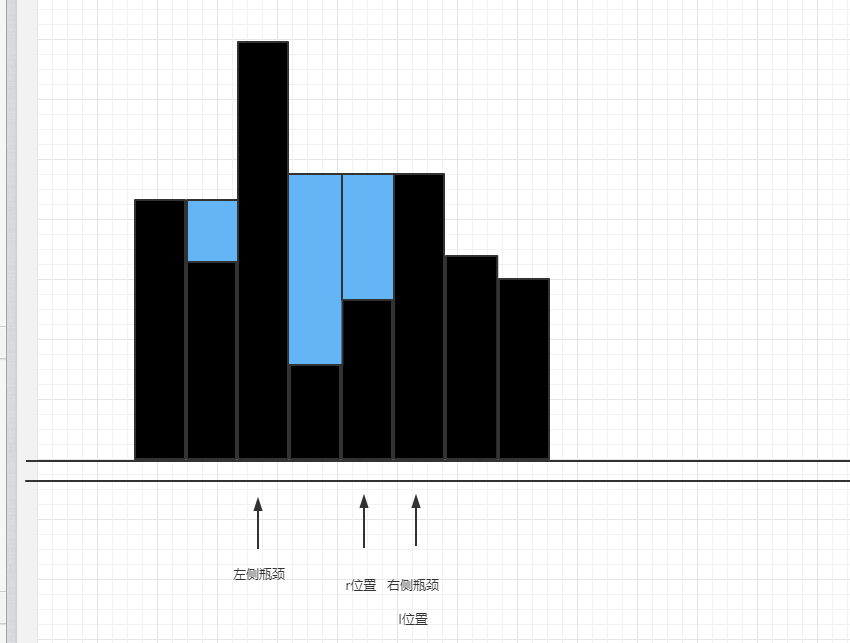
所有水收集完毕。

完整代码见

    public static int trap(int[] arr) {
        if (arr == null || arr.length <= 2) {
            return 0;
        }
        int result = 0;
        int l = 1;
        int r = arr.length - 2;
        int lMax = arr[0];
        int rMax = arr[arr.length - 1];
        while (l <= r) {
            if (lMax < rMax) {
                // 结算左侧
                result += Math.max(0, lMax - arr[l]);
                lMax = Math.max(lMax, arr[l++]);
            } else {
                // 结算右侧
                result += Math.max(0, rMax - arr[r]);
                rMax = Math.max(rMax, arr[r--]);
            }
        }
        return result;
    }

时间复杂度O(N)，空间复杂度O(1)。

LeetCode 407. 接雨水 II

主要思路

和一维的思路一样，二维接雨水问题也是先定位瓶颈，一维接雨水的瓶颈是从左右两端来定位，二维的瓶颈就是从矩阵的四周来定位。要找到四周的最小瓶颈，我们需要用一个小根堆（按值组织），将四周的值加入小根堆，弹出的值即为最小瓶颈。首先，我们需要包装一下原始矩阵，设计一个Node数据结构，用于存放原始矩阵中的某个值以及其位置信息。

    public static class Node {
        public int v; // 值
        public int i; // 行位置
        public int j; // 列位置

        public Node(int v, int i, int j) {
            this.i = i;
            this.j = j;
            this.v = v;
        }
    }

小根堆里面存的就是Node，按照Node的v来组织，

PriorityQueue<Node> heap = new PriorityQueue<>(Comparator.comparingInt(o -> o.v));

每当弹出一个Node的时候，将这个位置的上下左右（先确保不越界）进行结算，结算完成后，将已经结算的位置加入小根堆（已经加入过的位置就不用重复加入了），由于需要知道哪些位置加入过小根堆，所以设置一个二维的boolean数组，用于标志某个位置是否进入过。

boolean[][] isEntered = new boolean[m][n];

if (isEntered[i][j]) {
    // 某个位置进入过小根堆
} else {
    // 否则没有进入过
}

首先，我们将矩阵四周的点加入小根堆，并且把isEntered设置好

        // 以下两个for循环，是把四周都加入小根堆
        for (int i = 0; i < m; i++) {
            heap.offer(new Node(heightMap[i][0], i, 0));
            heap.offer(new Node(heightMap[i][n - 1], i, n - 1));
            isEntered[i][0] = true;
            isEntered[i][n - 1] = true;
        }
        for (int i = 0; i < n; i++) {
            heap.offer(new Node(heightMap[0][i], 0, i));
            heap.offer(new Node(heightMap[m - 1][i], m - 1, i));
            isEntered[0][i] = true;
            isEntered[m - 1][i] = true;
        }

然后我们设置一个max，用于标识此时最小瓶颈是哪个。接下来的流程就是：

每次从小根堆弹出一个元素，看下能否更新瓶颈值，且看其四面八方的位置上是否越界，如果没有越界，直接结算四面八方位置的值，累加到water这个变量中，同时把四面八方的Node加入小根堆，循环往复，直到小根堆为空。water的值即为收集到的水量。

完整代码见

    public static int trapRainWater(int[][] heightMap) {
        if (null == heightMap || heightMap.length <= 2 || heightMap[0].length <= 2) {
            return 0;
        }
        int m = heightMap.length;
        int n = heightMap[0].length;
        int max = 0;
        PriorityQueue<Node> heap = new PriorityQueue<>(Comparator.comparingInt(o -> o.v));
        boolean[][] isEntered = new boolean[m][n];
        // 以下两个for循环，是把四周都加入小根堆
        for (int i = 0; i < m; i++) {
            heap.offer(new Node(heightMap[i][0], i, 0));
            heap.offer(new Node(heightMap[i][n - 1], i, n - 1));
            isEntered[i][0] = true;
            isEntered[i][n - 1] = true;
        }
        for (int i = 0; i < n; i++) {
            heap.offer(new Node(heightMap[0][i], 0, i));
            heap.offer(new Node(heightMap[m - 1][i], m - 1, i));
            isEntered[0][i] = true;
            isEntered[m - 1][i] = true;
        }
        int water = 0;
        while (!heap.isEmpty()) {
            // 最薄弱的位置
            Node weakest = heap.poll();
            max = Math.max(weakest.v, max);
            int i = weakest.i;
            int j = weakest.j;
            if (i + 1 < m && !isEntered[i + 1][j]) {
                water += Math.max(0, max - heightMap[i + 1][j]);
                isEntered[i + 1][j] = true;
                heap.offer(new Node(heightMap[i + 1][j], i + 1, j));
            }
            if (i - 1 >= 0 && !isEntered[i - 1][j]) {
                water += Math.max(0, max - heightMap[i - 1][j]);
                isEntered[i - 1][j] = true;
                heap.offer(new Node(heightMap[i - 1][j], i - 1, j));
            }
            if (j + 1 < n && !isEntered[i][j + 1]) {
                water += Math.max(0, max - heightMap[i][j + 1]);
                isEntered[i][j + 1] = true;
                heap.offer(new Node(heightMap[i][j + 1], i, j + 1));
            }
            if (j - 1 >= 0 && !isEntered[i][j - 1]) {
                water += Math.max(0, max - heightMap[i][j - 1]);
                isEntered[i][j - 1] = true;
                heap.offer(new Node(heightMap[i][j - 1], i, j - 1));
            }
        }
        return water;
    }

    public static class Node {
        public int v;
        public int i;
        public int j;

        public Node(int v, int i, int j) {
            this.i = i;
            this.j = j;
            this.v = v;
        }
    }

空间复杂度O(M*N)，时间复杂度是O(M*N*log(M+N))。

更多

算法和数据结构笔记