完美洗牌问题

完美洗牌问题

作者：Grey

原文地址:

博客园：完美洗牌问题

CSDN：完美洗牌问题

问题描述

给定一个长度为偶数的数组arr，假设长度为\(N*2\)

左部分：arr[L1...Ln]

右部分：arr[R1...Rn]

请把arr调整成arr[L1,R1,L2,R2,L3,R3,...,Ln,Rn]

要求时间复杂度O(N)，额外空间复杂度O(1)

OJ见：LeetCode 1470. 重新排列数组

主要思路

解决完美洗牌问题之前，我们需要先解决另外一个相对简单的算法问题：剑指 Offer 58 - II. 左旋转字符串

简言之，如何原地让一个数组部分旋转，比如：

[b,c,a,g,f,q]

我们需要让区间[0...2]数组和区间[3...5]的数组进行旋转，而且不能依赖辅助数组，旋转后的结果是

[g,f,q,b,c,a]

解决这个算法的思路是，首先，实现一个函数，反转数组

reverse(char[] arr, int l, int r)

这个函数的功能是将arr这个字符串进行原地反转，我们可以通过两个指针来实现

public void reverse(char[] str, int l, int r) {
    while (l < r) {
        swap(str, l++, r--);
    }
}

有了这个函数，我们可以先让[0...2]区间先做reverse操作，然后再让[3...5]区间做reverse操作，然后整体[0...5]做reverse操作，就实现了部分旋转。

第一步，区间[0...2]做reverse操作，得到

[q,f,g,b,c,a]

第二步，区间[3...5]做reverse操作，得到

[q,f,g,a,c,b ]

第三步，区间[0...5]做reverse操作，得到

[b,c,a,g,f,q]

剑指 Offer 58 - II. 左旋转字符串完整代码如下

public class LeetCodeCN_0058_LCOF {
    public String reverseLeftWords(String s, int n) {
        char[] str = s.toCharArray();
        rotate(str, 0, n - 1, s.length() - 1);
        return String.valueOf(str);
    }

    public void rotate(char[] arr, int L, int M, int R) {
        reverse(arr, L, M);
        reverse(arr, M + 1, R);
        reverse(arr, L, R);
    }

    public void reverse(char[] str, int l, int r) {
        while (l < r) {
            swap(str, l++, r--);
        }
    }

    public void swap(char[] str, int l, int r) {
        char tmp = str[l];
        str[l] = str[r];
        str[r] = tmp;
    }
}

有了这个算法铺垫，要解决完美洗牌问题，还需要推导一个公式，假设原数组是

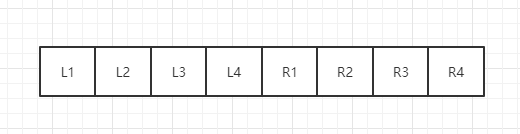
那么经过洗牌后，要调整后的数组是

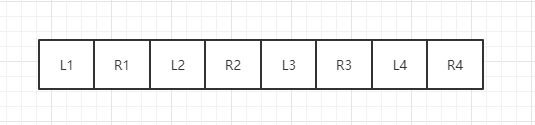
通过观察可知，对于原数组任何一个位置i，在调整后的数组应该位于j位置，其中i和j有如下关系，假设数组长度为N，注：i和j都是从1开始算，而不是从0开始算

j = (2 * i) % (N + 1);

所以，针对上述数组，遍历每一个位置，都可以找到这个位置需要移动到的位置是哪里，但是会出现一种情况，比如这个数组，

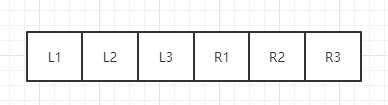
通过上述公式
L1顶替了L2的位置，把L2置换出来
L2被置换出来以后，顶替了R1的位置
R1被置换出来以后，顶替了L1的位置，此时，L1,L2,R1形成了一个环。

形成了如下情况

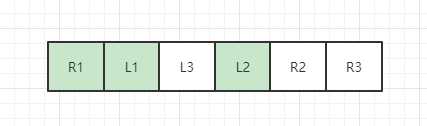
其中标绿的部分形成了一个环，我们还需要找到下一个未处理的位置，即L3位置，继续调用上述公式，

通过上述公式
L3顶替了R3的位置，把R3置换出来
R3被置换出来以后，顶替了R2的位置
R2被置换出来以后，顶替了L3的位置，此时，L3,R2,R3形成了一个环。

形成了如下情况

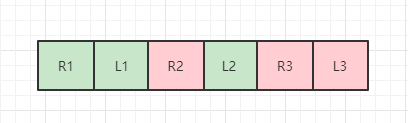
然后利用前面提到的部分数组旋转的方式，两两交换位置，得到最后的结果

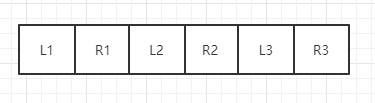
所以，针对这样有环的情况，我们需要找到所有的入环点，然后依次调用公式，把元素放到正确的位置，在这里，需要引入一个结论：

当数组长度满足N = 3^(k) - 1 的时候，环的出发点1,3,9...3^(k-1)

例如：

当数组长度为8的时候，环的出发点分别是：1，3

当数组长度为13的时候，环的出发点分别是：1，3，9

但是，数组长度不满足这个公式的时候，环的出发点就没有这个规律，如果数组长度不满足这个公式，则需要获取整个数组离满足这个公式最近的长度来进行操作，例如，数组的长度为12，不满足3^(k) - 1，

这个长度为12的数组距离最近的一个满足公式的位置是8（即：3^2 - 1)，那么可以将这个长度为12的数组分成两部分，一部分长度是8，另外一部分长度是4，

长度为8的数组，应该是左边四个（L1，L2，L3，L4），右边四个（R1，R2，R3，R4），所以，我们对这个数组做一次反转，把区间[L5,L6]和区间[R1,R2,R3,R4]做一次反转，得到

标红部分，就可以通过公式得到入环点是L1和L3，然后利用入环点调用公式得到每个位置调整后的位置

剩余长度为4的数组，同样找到离4最近的，满足条件的长度是2（即：3^1 - 1), 然后将长度为4的数组同样做上述处理，得到

[L5,R5]这个数组长度为2，满足公式，带入公式得到

[L6,R6]同理，最后，得到如下数组

并且将整个数组两两交换，得到最终满足条件的数组

完整代码

public class LeetCode_1470_ShuffleTheArray {
    public int[] shuffle(int[] arr, int n) {
        shuffle(arr);
        for (int i = 0; i < arr.length; i+=2) {
            reverse(arr,i,i+1);
        }
        return arr;
    }
    
    public static void shuffle(int[] arr) {
        if (arr == null || arr.length == 0 || (arr.length & 1) != 0) {
            return;
        }
        shuffle(arr, 0, arr.length - 1);
    }

    public static void swap(int[] nums, int L, int R) {
        if (nums == null || nums.length <= 1 || R == L) {
            return;
        }
        nums[L] = nums[L] ^ nums[R];
        nums[R] = nums[L] ^ nums[R];
        nums[L] = nums[L] ^ nums[R];
    }

    public static void shuffle(int[] arr, int L, int R) {
        while (R - L + 1 > 0) {
            int len = R - L + 1;
            int base = 3;
            int k = 1;
            while (base <= (len + 1) / 3) {
                base *= 3;
                k++;
            }
            int half = (base - 1) / 2;
            int mid = (L + R) / 2;
            rotate(arr, L + half, mid, mid + half);
            toNext(arr, L, base - 1, k);
            L = L + base - 1;
        }
    }

    // i位置下一个位置应该去哪里
    // i 从1开始，而不是从0开始!!!
    private static int findNextIndex(int i, int N) {
        // return (2 * i) % (N + 1);
        if (i <= N / 2) {
            return 2 * i;
        }
        return (i - N / 2) * 2 - 1;
    }

    private static void toNext(int[] arr, int start, int len, int k) {
        for (int i = 0, trigger = 1; i < k; i++, trigger *= 3) {
            int pre = arr[start + trigger - 1];
            int next = findNextIndex(trigger, len);
            while (next != trigger) {
                int t = arr[next + start - 1];
                arr[next + start - 1] = pre;
                pre = t;
                next = findNextIndex(next, len);
            }
            arr[next + start - 1] = pre;
        }
    }

    // @see LeetCodeCN_0058_LCOF
    // L..M部分和M+1..R部分互换
    public static void rotate(int[] arr, int L, int M, int R) {
        reverse(arr, L, M);
        reverse(arr, M + 1, R);
        reverse(arr, L, R);
    }

    // L..R做逆序调整
    public static void reverse(int[] arr, int L, int R) {
        while (L < R) {
            swap(arr, L++, R--);
        }
    }
}

类似问题

牛客：完美洗牌

LeetCode 324. Wiggle Sort II

更多

算法和数据结构学习笔记

算法和数据结构学习代码