有效括号匹配问题
有效括号匹配问题
作者: Grey
原文地址:
LeetCode 20. 有效的括号
主要思路
使用一个栈,然后开始遍历整个序列,入栈和出栈规则如下:
- 遇到左括号入栈
- 遇到右括号,从栈里先弹出一个元素,如果弹出的元素和这个右括号正好匹配,则继续,如果不匹配,直接返回不是合法序列
走完整个遍历后,栈为空,则是合法序列,栈不为空,则不是合法序列。
在遍历过程中(还没遍历结束),一旦某个时间点栈为空,则直接返回不合法序列。
完整源码:
public static boolean isValid(String s) {
if (s == null || s.length() == 0) {
return true;
}
char[] strs = s.toCharArray();
Deque<Character> stack = new ArrayDeque<Character>();
int len = strs.length;
for (int i = 0; i < len; i++) {
if (isLeft(strs[i])) {
stack.push(strs[i]);
} else {
if (stack.isEmpty()) {
// 遍历的中间过程,一旦发现栈空,则直接返回false
return false;
} else if (!isMatch(stack.poll(), strs[i])) {
return false;
}
}
}
return stack.isEmpty();
}
public static boolean isLeft(char c) {
return '(' == c || '{' == c || '[' == c;
}
public static boolean isMatch(char left, char right) {
return (left == '[' && right == ']') || (left == '(' && right == ')') || (left == '{' && right == '}');
}
注:这里没有使用stack,而是用的Deque,原因在这里:Java Deque vs. Stack
We've seen that the Stack class is a subclass of java.util.Vector. The Vector class is synchronized. It uses the traditional way to achieve thread-safety: making its methods “synchronized.” As its subclass, the Stack class is synchronized as well. On the other hand, the Deque interface is not thread-safe.So, if thread-safety is not a requirement, a Deque can bring us better performance than a Stack.
简言之,Deque使用无锁操作,线程不安全,但是效率更高,如果不要求线程安全,Deque是更好的选择。
LeetCode 32. 最长有效括号
主要思路
设置dp数组,长度和原始字符串的长度一样,
dp[i]表示:必须以i位置字符结尾的字符串的最长有效括号子串的长度是多少。
显然有:
dp[0] = 0; // 必须以0位置的字符结尾的最长有效括号子串是0
dp[1] = (str[1] == ')' && str[0] == '('?2:0); // 必须以1位置的字符结尾的最长有效括号子串,如果满足`()`则为2,否则都是无效子串,返回0
然后看任意一个普遍位置i
如果i位置的字符是(,则
dp[i] = 0
因为一个有效的括号子串的结尾不可能是(
如果i位置的字符是),则要分以下几种情况,假设我们以i=6为例,如下示例图
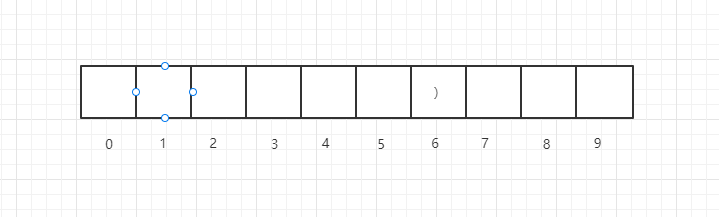
此时,如果i-1即5位置是(,如下示例
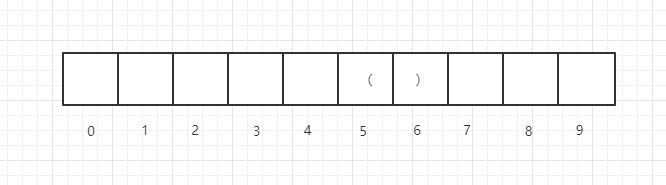
那么i位置的一种决策是:i位置和i-1先组成一个有效括号子串,长度是2,然后加上dp[i-2]的值,即:
dp[i] = dp[i-2] + 2
如果i-1位置,即5位置是),如下示例:

假设dp[i-1]即:dp[5] = 4,即str[2]位置一定是(,如下图
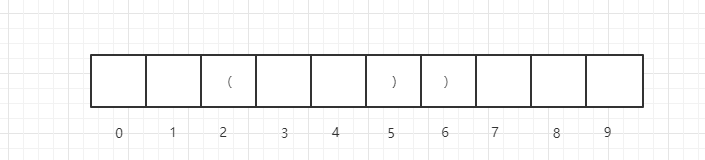
此时,分两种情况,如果str[1]位置上是(,即:
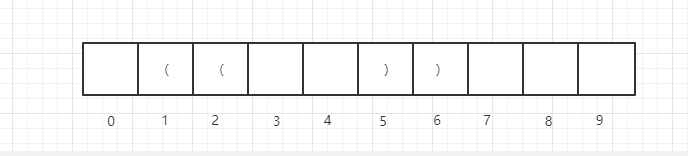
那么此时:
dp[6] = dp[5] + 6位置上的一个右括号+1位置上的一个左括号 + dp[0],即:dp[i] = dp[i-1] + 2 + dp[(i-1) - dp[i-1] - 1]
如果str[1]位置上是),即:
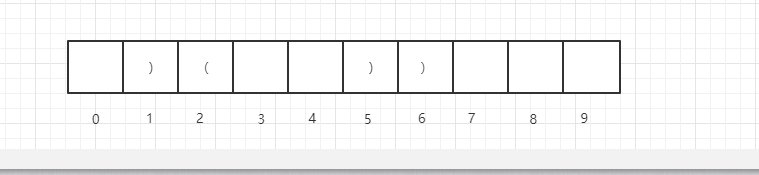
那么此时,dp[1]一定等于0,因为如果dp[1]不等于0,那么就意味着以1结尾的最长有效括号子串大于0,那么dp[5]就不止可以扩到2位置了,与我们假设的条件矛盾,所以,当dp[6]为),且dp[1]为)的时候,dp[6]一定等于0。
自此,所有可能性分析完毕。完整代码如下:
public static int longestValidParentheses(String s) {
if (s == null || s.length() <= 1) {
return 0;
}
char[] str = s.toCharArray();
// dp[i]:必须以i位置符号结尾的字符串,最长有效括号串长度是多少
int[] dp = new int[str.length];
// dp[0] = 0, dp[1] = 0
dp[1] = str[0] == '(' && str[1] == ')' ? 2 : 0;
int ans = dp[1];
for (int i = 2; i < str.length; i++) {
if (str[i] == ')') {
// 这才是有效情况
if (str[i - 1] == '(') {
dp[i] = dp[i - 2] + 2;
} else {
if ((i - 1) - dp[i - 1] >= 0 && str[(i - 1) - dp[i - 1]] == '(') {
dp[i] = dp[i - 1] + 2 + ((i - 1) - dp[i - 1] > 0 ? dp[(i - 1) - dp[i - 1] - 1] : 0);
}
}
}
ans = Math.max(ans, dp[i]);
}
return ans;
}
更多
本文来自博客园,作者:Grey Zeng,转载请注明原文链接:https://www.cnblogs.com/greyzeng/p/16353363.html

