有序表和搜索二叉树

有序表和搜索二叉树

作者: Grey

原文地址：

博客园：有序表和搜索二叉树

CSDN：有序表和搜索二叉树

说明

本文的所有图例见：processon: 有序表和搜索二叉树

搜索二叉树

定义：任何一个节点，左树都比这个节点小，右数都比这个节点大，经典搜索二叉树是没有重复值的，有重复值就压在一起

构造搜索二叉树方法：

1. 比当前节点大，就往右边滑，滑到空就把节点加上
2. 比当前节点小，就往左边滑，滑到空就把节点加上

搜索二叉树的增删改，注：改可以转换成删掉再增加

搜索二叉树的删除流程如下

1. 未找到，直接返回
2. 如果找到，既没有左孩子，也没有右孩子，直接删掉
3. 如果找到，有右无左，右孩子提拔
4. 如果找到，有左无右，左孩子提拔
5. 如果找到，有左有右，则找右树的最左节点（后继节点）替代被删除位置，后继节点的右孩子直接给新的右树最左节点。

搜索二叉树的删除示例图如下，假设原搜索二叉树是如下结构：

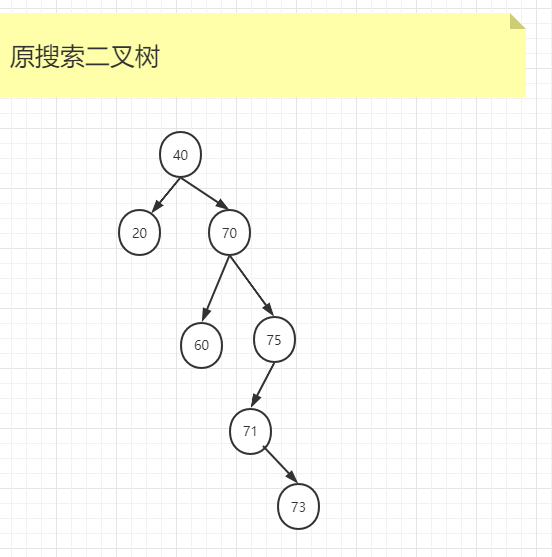
如果要删除60号节点，因为60号节点既没有左孩子，也没有右孩子，所以直接删除即可。

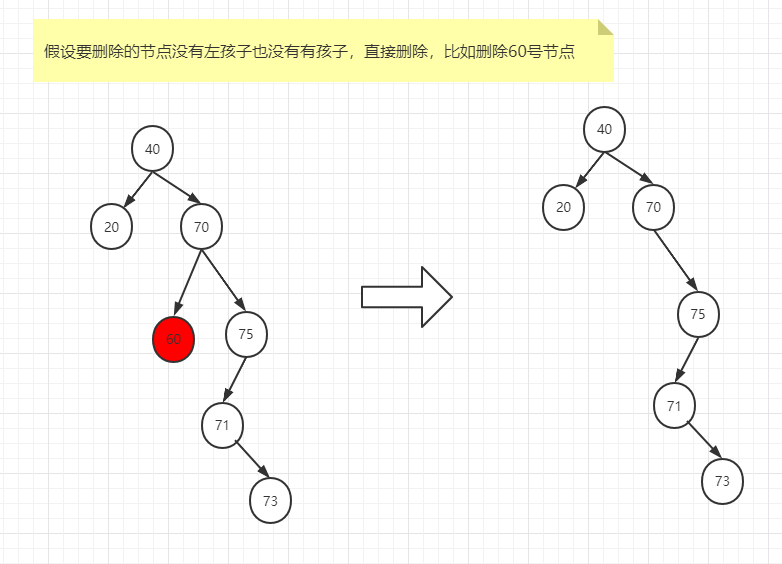
如果要删除75号节点，因为75号节点只有左孩子，所以直接用75号节点的左孩子替代被删除的75号节点位置即可。

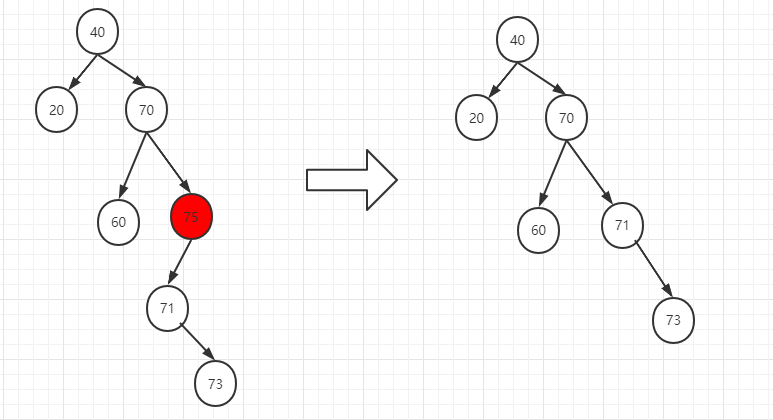
如果要删除71号节点，因为71号节点只有右孩子，所以直接用其右孩子替代即可。

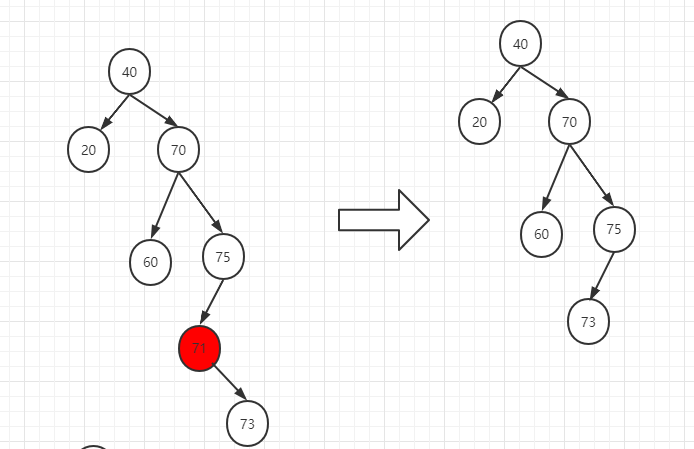
如果要删除的节点是70号节点，因为70号节点既有左孩子又有右孩子，所以，首先要找到70号节点的后继节点（即71号位置）

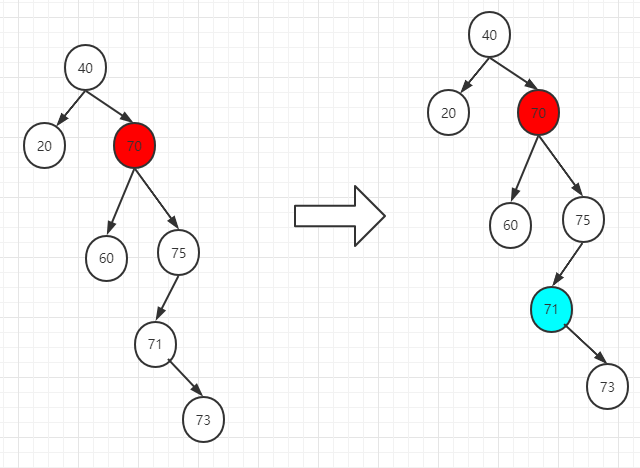
然后用后继节点替代被删除节点的位置，同时，把后继节点的右孩子给新的右侧最左节点（即75号节点位置）

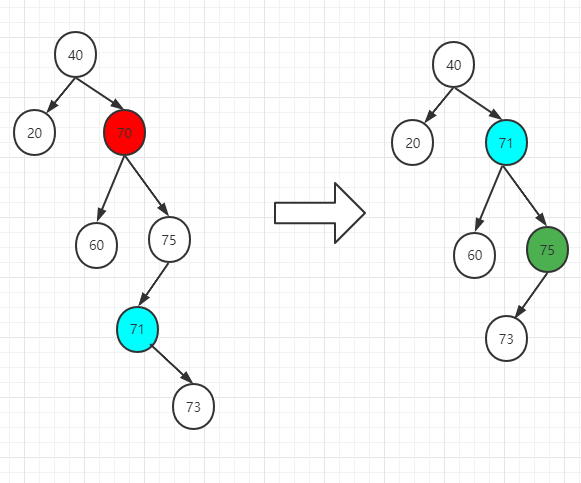
注意delete方法在删除的时候，需要考虑后继节点是直接的右孩子还是距离需要删除的节点有一定距离的节点！

搜索二叉树的最大问题是： 输入状况决定性能，如果输入状况比较好，树是平衡的，输入状况比较差，树不是平衡的，严格的平衡性指的是：任何一个节点左树右树高度差不超过1，比如用户输入的数据如下[1,2,3,4,5]，形成的搜索二叉树就退化成了如下链表结构

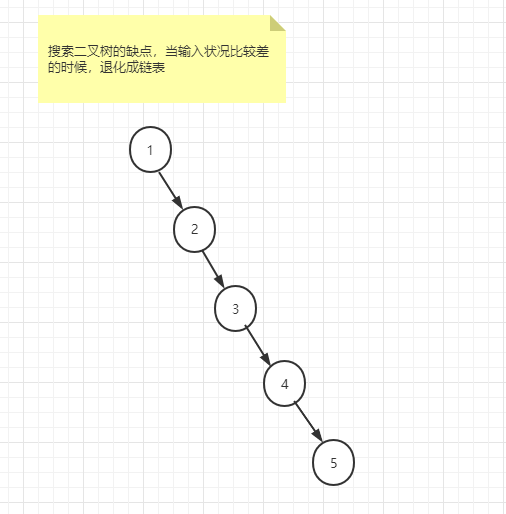
所以需要引入自平衡的功能， 即平衡搜索二叉树

平衡搜索二叉树

平衡搜索二叉树要满足如下两种情况

1. key按序组织
2. 增删改O(logN)

AVL树, SBT, 红黑树都是平衡搜索二叉树的一种具体实现，增删改的时间复杂度均为O(logN)

平衡搜索二叉树在搜索二叉树的基础上增加了两个操作，左旋和右旋。

左旋和右旋要针对具体节点说

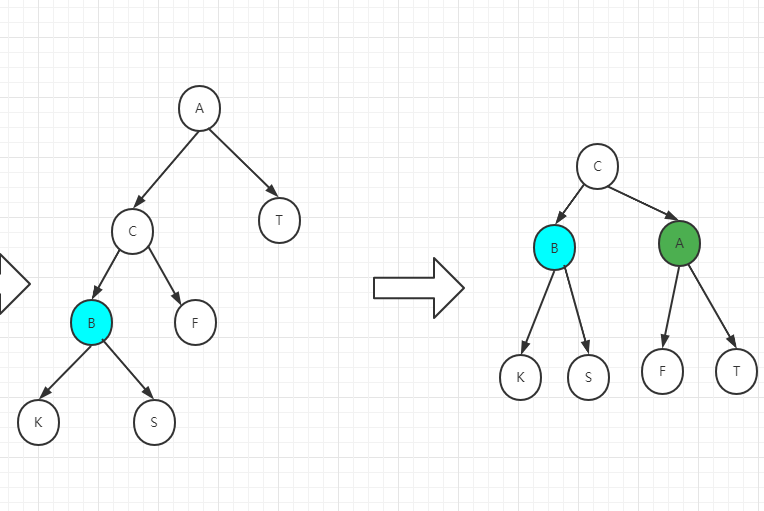
左旋示例，如下搜索二叉树，如果针对A节点左旋

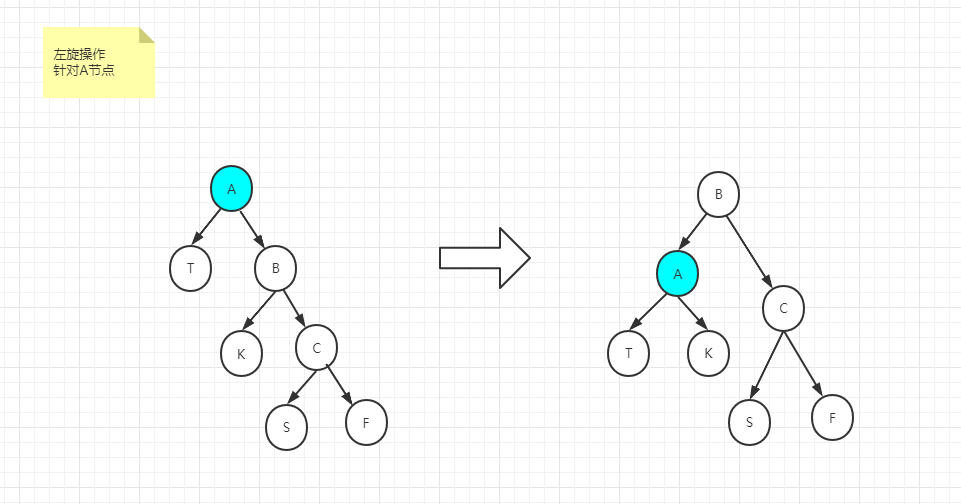
如下搜索二叉树，如果针对A节点右旋

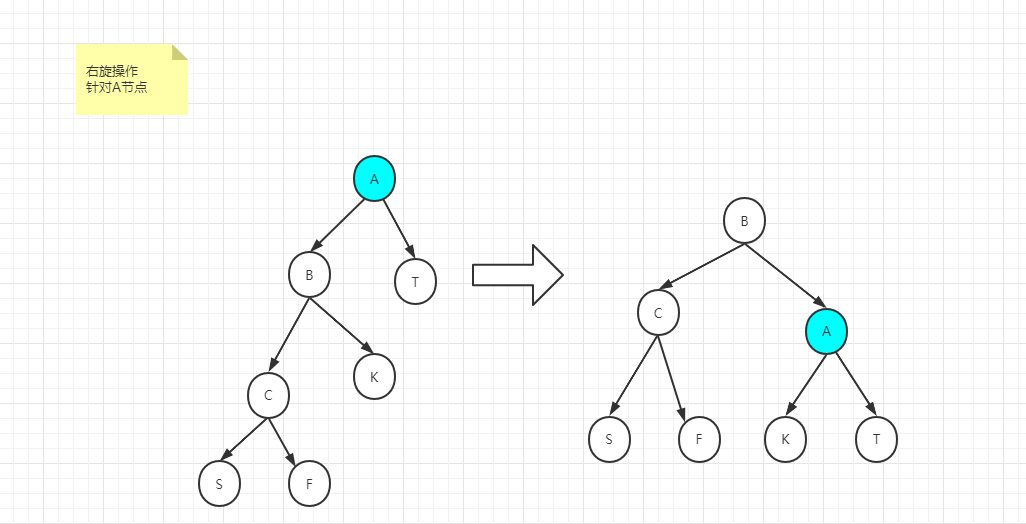
AVL树，SBT，红黑树有各自的平衡性定义，但是底层的操作都是左旋和右旋。

AVL树

AVL树最严格的平衡性，左右高度只差绝对值小于2。

AVL树的增删节点和平衡二叉树一样，只是在调用增删操作后，AVL树有自己的调整策略。

AVL树平衡性破坏有如下几种类型

LL

解决办法：只做一次右旋，示例：

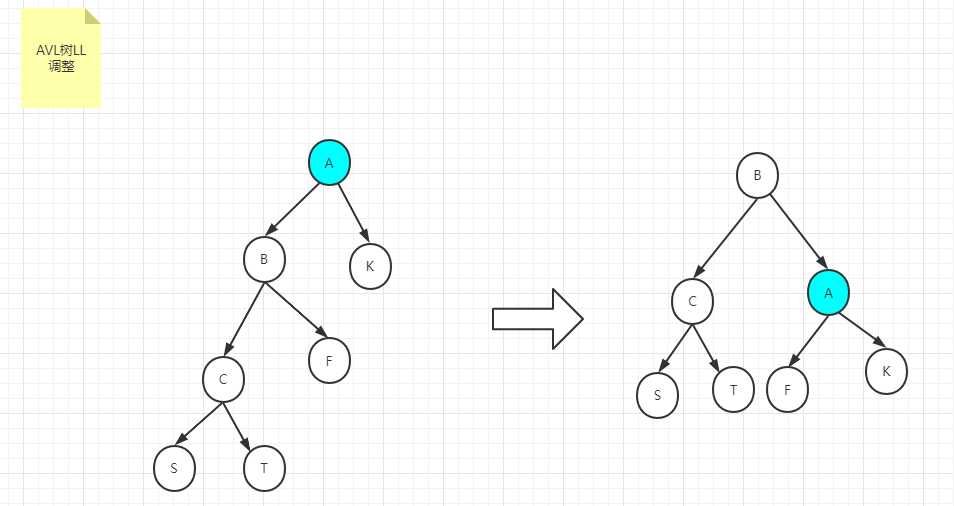
RR同理，只做一次左旋即可。

LR

LR情况示例

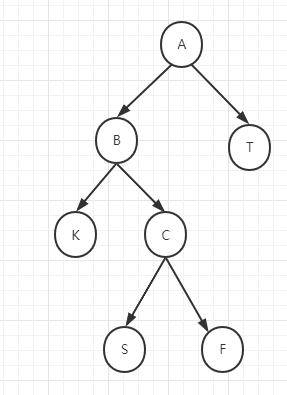
先对B进行一次左旋

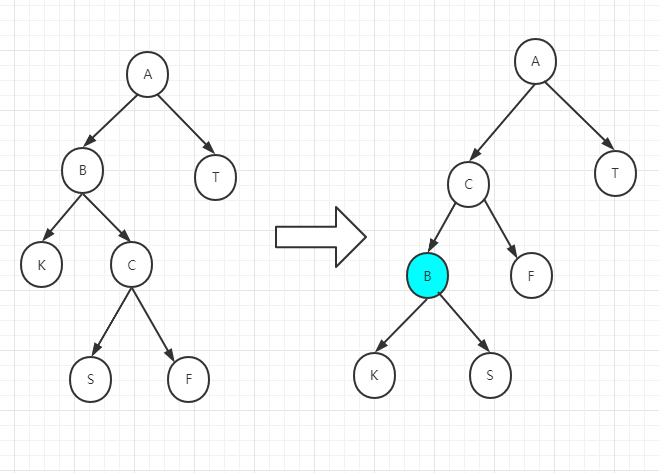
再对头部A进行一次右旋

RL同理

LL+LR

对于既是LL，又是LR的情况，例如：

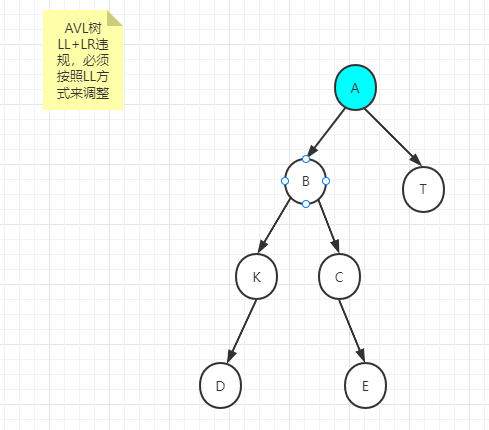
在这样的情况下，一定要按照LL方式来调整。

如上例，调整规则为：

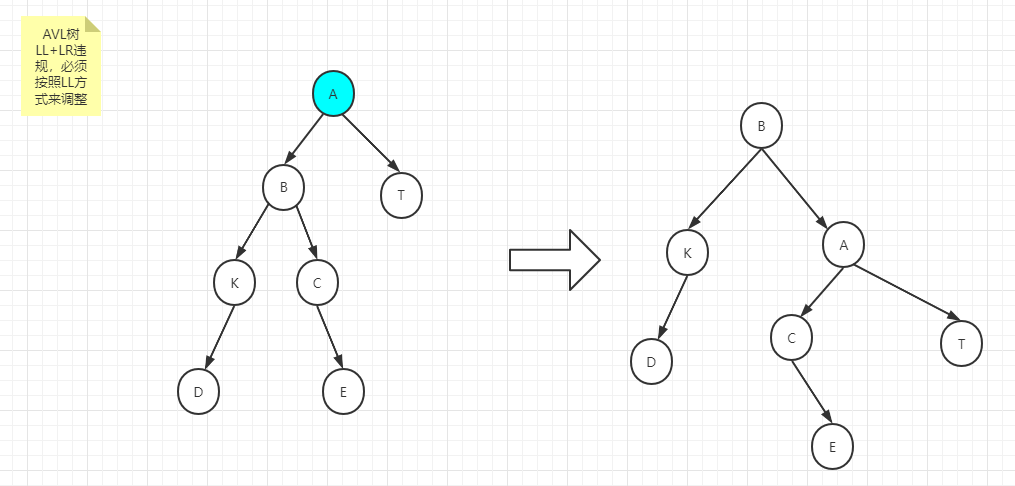
同理，对于既是RR，又是RL的情况，也要按照RR方式来调整。

AVL调整过程

在增加节点的时候，插入位置的父节点一直往上查，看下每个节点是否违规。

在删除节点的时候，删除位置的父节点一直往上查，看下每个节点是否违规，如果删除节点包含左右孩子，那么必须从这个节点的后继节点往上一直查。

AVL实现代码

AVLTreeMap

SBT

SBT全称Size Balanced Tree，任何一个叔节点子树节点数不少于他的侄子节点个数（叔侄关系如下示例图），即左右树节点数的规模差不多就是2倍加1

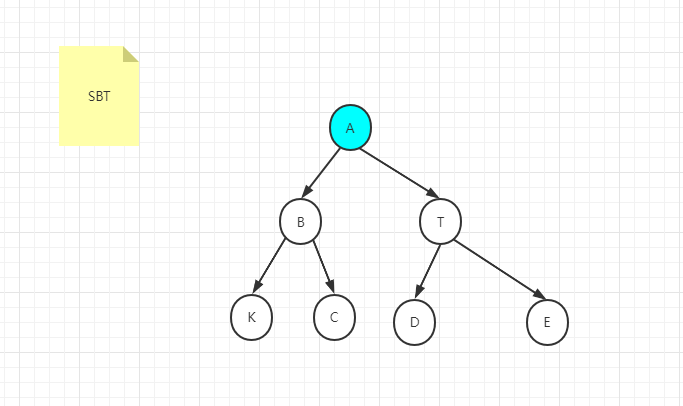
AVL树维持的是每个节点的高度，而SBT维持的是每个节点子树节点个数。

SBT的违规情况也有四种（LL，LR，RR，RL）

SBT的LL违规和调整过程

父的左孩子的左孩子的节点个数大于父亲右孩子的节点数，例如：

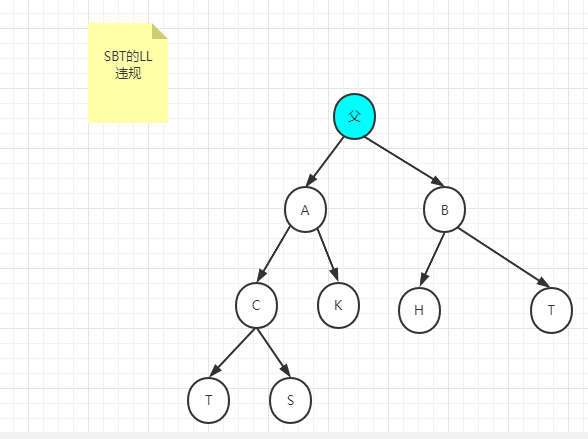
所以，上述搜索二叉树在做完AVL调整后，为如下情况：

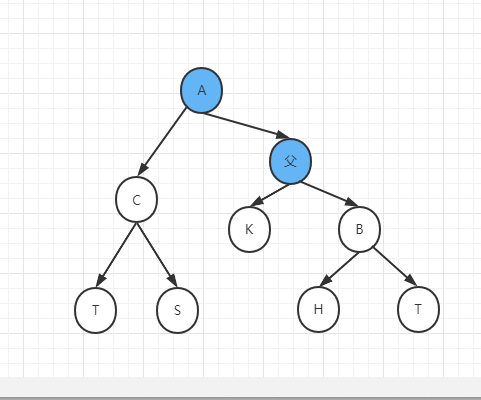
按AVL的方式调用完毕后，看谁的孩子发生了变化，如上例，是A和父两个点的孩子发生变化，就递归调用m(A), m(父), LR, RR, RL调整方式一样，都是通过AVL对应的调整方式，然后查看是否有节点的孩子发生变化，如果发生变化，对这些节点做递归调用。

注：SBT在删除节点的时候，不做平衡性调整，只在add节点的时候做平衡性调整，因为有递归行为。所以每次add会自动调整平衡性

SBT的实现代码

SizeBalancedTreeMap

有序表的使用

【牛客】找工作问题

问题描述：NowCoder_FindJob

代码参考：NowCoder_FindJob

【LeetCode 218】天际线问题

问题描述: LeetCode_0218_TheSkylineProblem

代码参考：LeetCode_0218_TheSkylineProblem

【LeetCode 327】区间和的个数

问题描述：LeetCode_0327_CountOfRangeSum

代码参考：LeetCode_0327_CountOfRangeSum

注：本题既可以用改写归并排序的方法来解，也可以通过改写有序表来解。

【LeetCode 480】滑动窗口的中位数

问题描述：LeetCode_0480_SlidingWindowMedian

代码参考：LeetCode_0480_SlidingWindowMedian

更多

算法和数据结构笔记

参考资料

算法和数据结构体系班-左程云