使用 AC 自动机解决文章匹配多个候选词问题

使用 AC 自动机解决文章匹配多个候选词问题

作者：Grey

原文地址:

博客园：使用AC自动机解决文章匹配多个候选词问题

CSDN：使用AC自动机解决文章匹配多个候选词问题

解决的问题

KMP算法用于单个字符串匹配，AC自动机用于文章中匹配多个候选词。

例如：

文章为："abcdhekskdjfafhasldkflskdjhwqaeruv"

候选词列表为：["dhe", "he", "abcdheks", "abdcdheks"]

需要返回文章中包含的候选词列表：["dhe", "he", "abcdheks"]

流程

第一步，先将候选词先建立前缀树。

第二步，以宽度优先遍历的方式把前缀树的每个节点设置fail指针, 规定：头节点的fail指针指向null, 头节点孩子的fail指针指向头节点。

第三步，除了头节点和头节点的孩子节点，其他节点的fail指针设置逻辑为：来到X节点的时候，是设置X孩子的fail指针。

case 1：

假设X节点通过b这条边指向了它的孩子C，X的fail指针指向的节点假设为Y，Y有走向b的路，且Y走向b的路是指向的Z，那么C的fail指针指向Z，如果Y没有走向b的路，那么就看Y的fail指针指向的节点有没有走向b的路，依次往复，如果走到null都没有，那么进入case 2

流程图如下：

找一次就找到fail指针的情况如下图

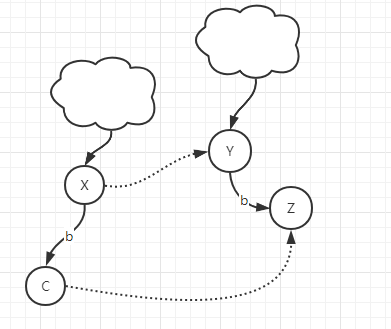
多次跳转才能找到fail指针的情况如下图

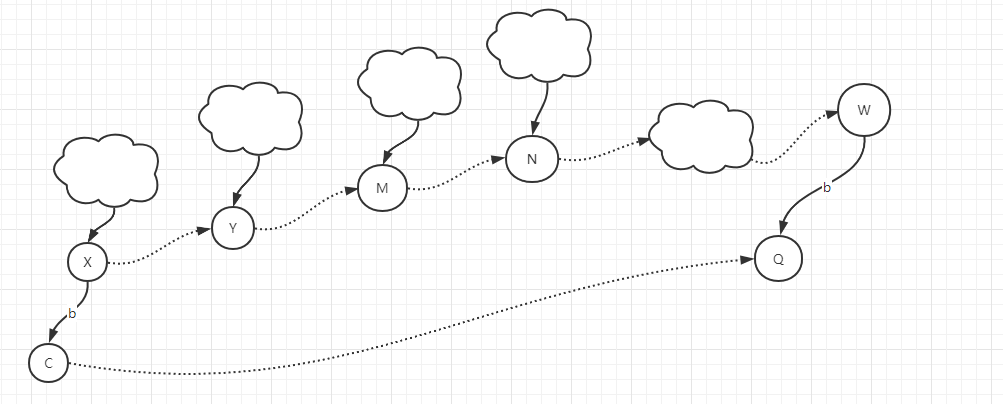
case 2：

如果X的fail指针指向null，那么就把X的孩子C指向头节点

一些示例

如下为候选词构造前缀树和fail指针的一些示例，其中虚线表示节点fail指针的指向位置，黑色点表示候选词结尾位置。

示例一 ["abc","bkf","abcd","bkc"]

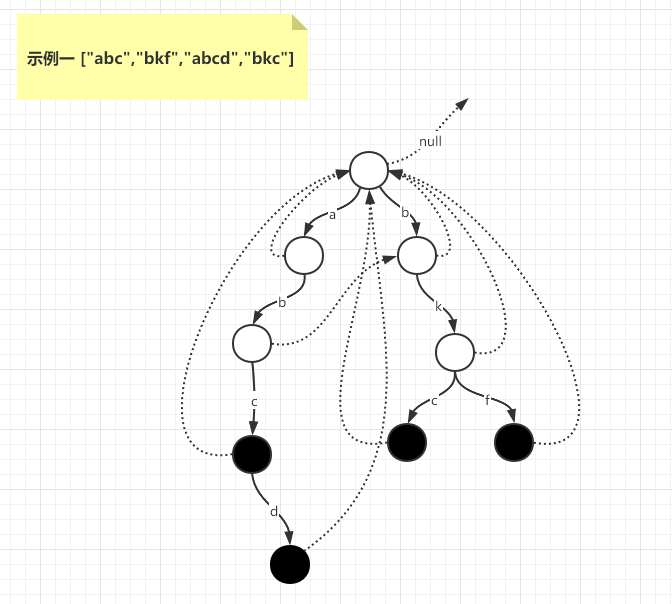
示例二 ["abcde","cde","e"]

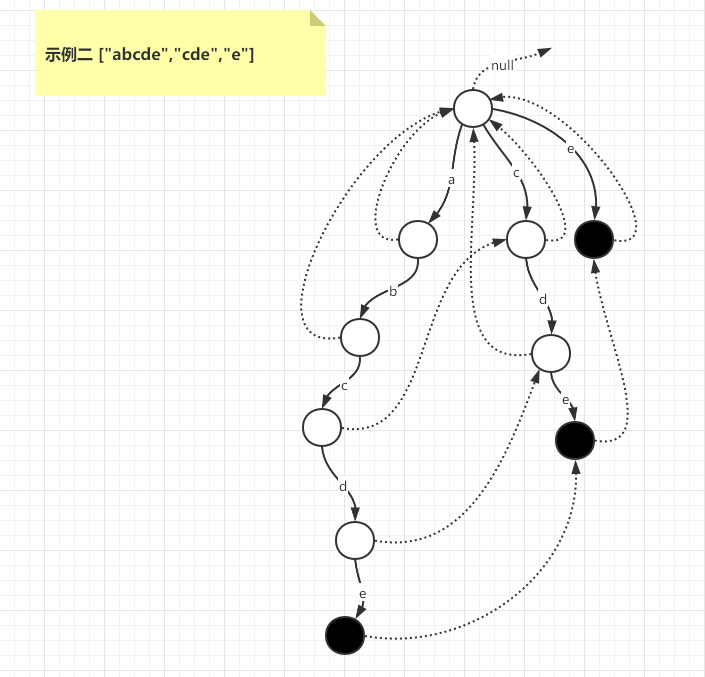
示例三 ["abcde","bcde","cde","de","e"]

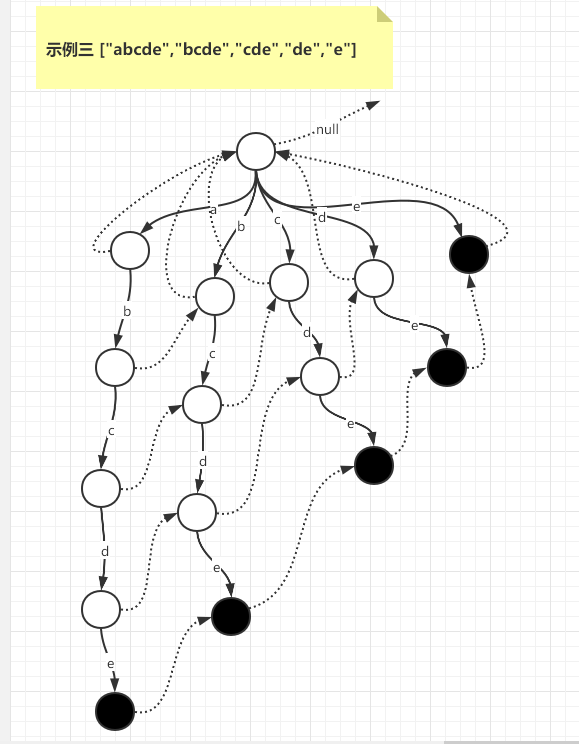
示例四 ["abcdef"，"cdef"，"ex"]

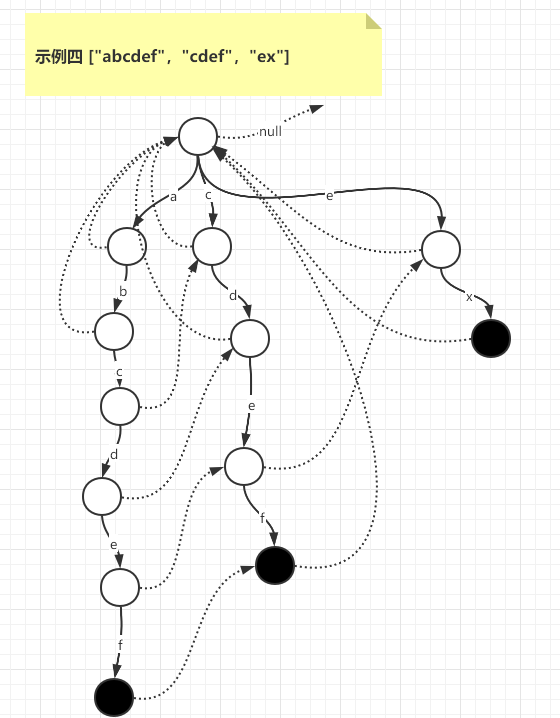
示例五 ["abcde"，"bcdf"，"cdtks"]

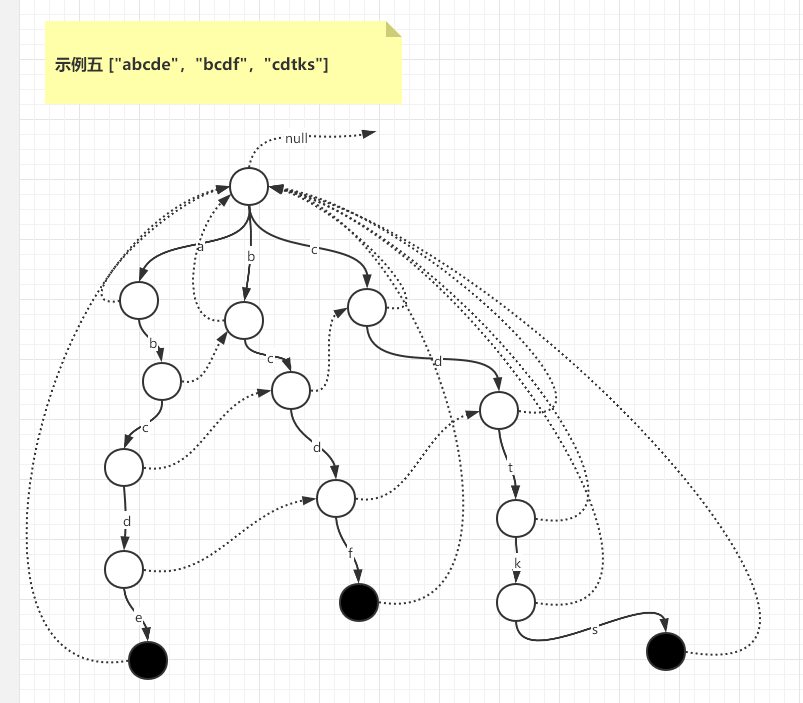
示例六 ["abc","abcde","abcd","bc","cd"]

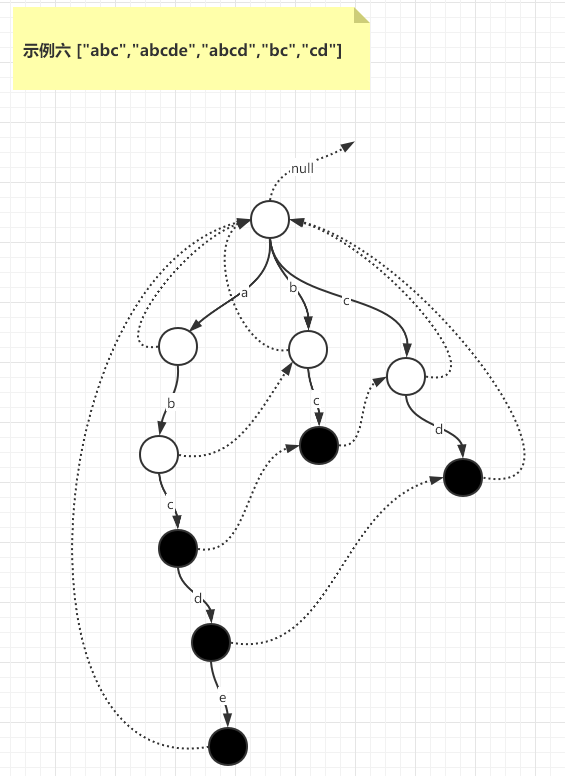
示例七 ["abck","bct","st"]

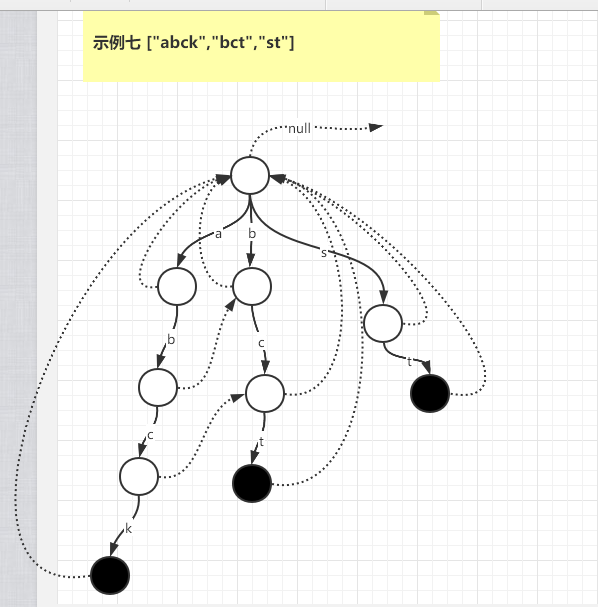
fail指针的含义

假设要以这个字符结尾，哪一个另外的后缀串和其前缀串完全相等

假设["abcde","bcde","cde","de","e"]，所以abcde中e的fail指针指向bcde中的e，因为以abcde中以e结尾的后缀有bcde和候选词bcde的前缀匹配最长。

匹配规则

每次来到一个节点，根据fail指针转一圈，如果有描黑的点（结尾点）就收集答案，同时把结尾标志为已处理（防止重复收集），匹配失败的时候，要顺着fail指针蹦到另外一条路径上继续匹配。

举例

文章："abcde"

候选词：["abc","abcde","abcd","bc","cd"]

流程：

第一步，先对候选词建立前缀树并连接好fail指针，建立好以后，如下图

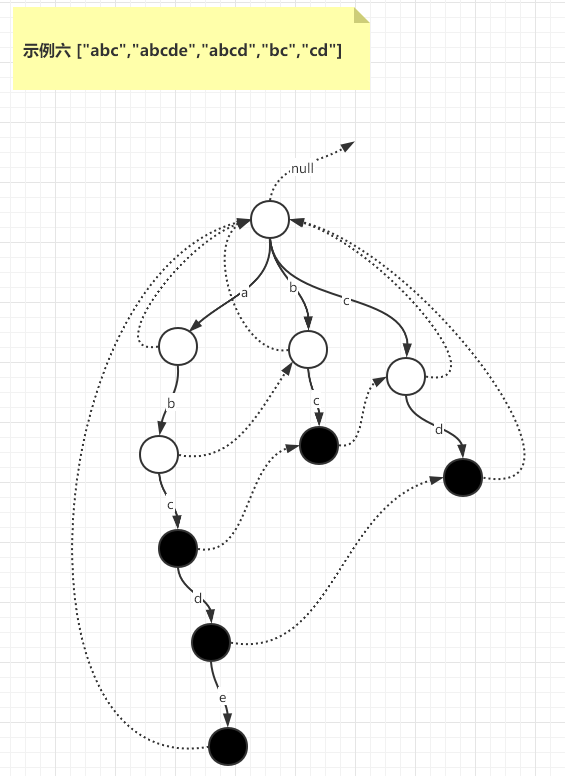
第二步，文章的逐个位置进行匹配。来到第一个字符a, 前缀树中有走向a字符方向的路。如下图，走到2号点位置：

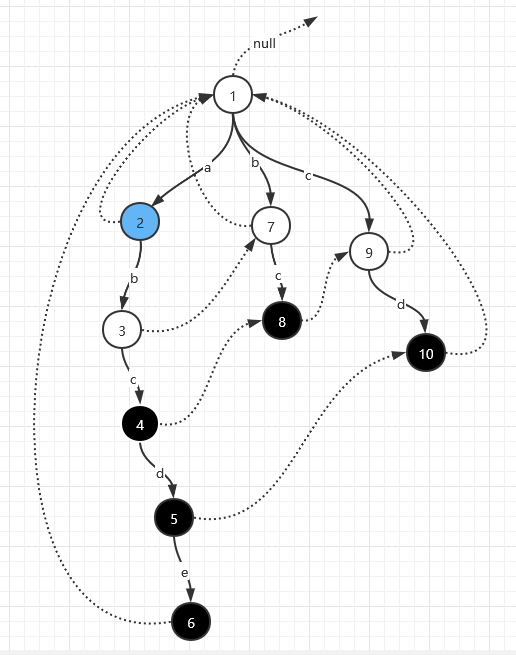
然后停在2号点位置，顺着fail指针走一圈，如果有黑色点（结束点）就收集答案。所以，在2号点位置，顺着fail指针走一圈分别要经过2号点，1号点，均不是结尾点，所以没有答案收集。然后再匹配文章的下一个字符b, 前缀树来到如下3号位置节点：

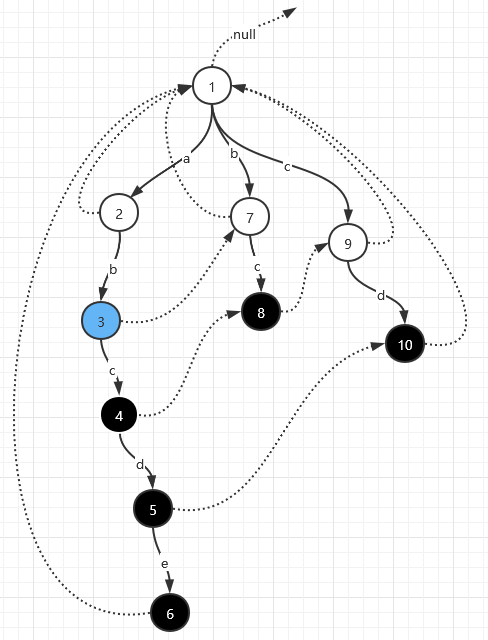
然后停在3号节点，顺着fail指针走一圈，分别会经历7号节点和1号节点，均不是结尾点，所以未收集到答案。

继续匹配文章下一个节点c，前缀树来到4号位置：

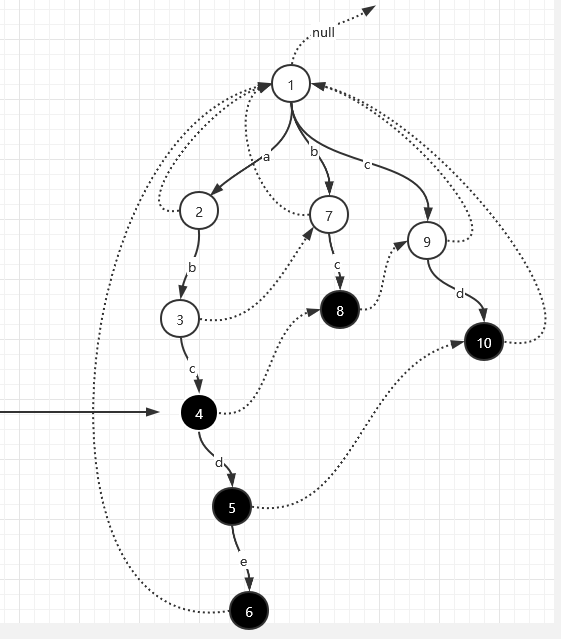
然后停在4号位置，顺着fail指针走一圈，分别经历了4号节点，8号节点，9号节点和1号节点，其中4号和8号是结尾点（表示abc的结尾和bc的结尾），所以收集到两个答案abc和bc。

继续匹配文章中的d字符，来到5号节点

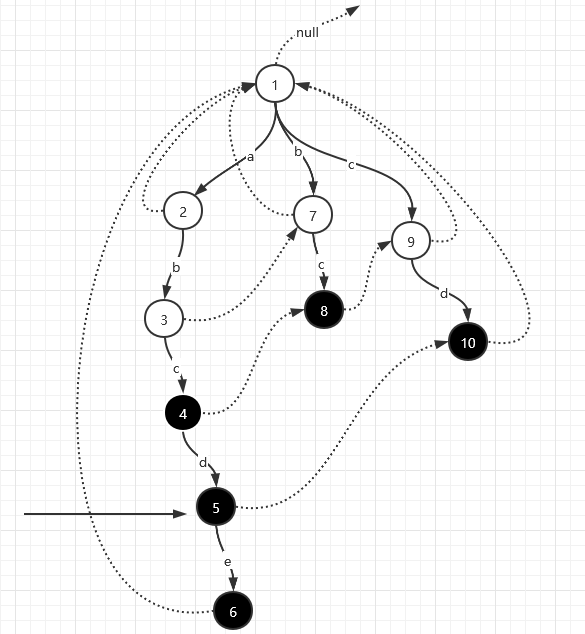
然后停在5号节点上，顺着fail指针走一圈，会经历5，10，1号节点，5和10号节点分别是abcd和cd的结尾，所以收集到了abcd和cd两个答案。

最后来到文章最后一个节点e，即到6号点位置

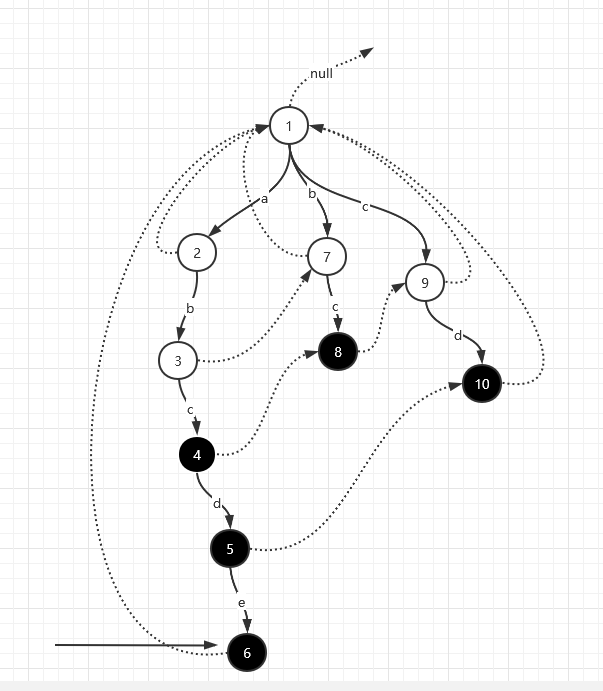
停在6号点位置，顺着fail指针走，经过6号和1号，6号为abcde的结尾，所有收集到了abcde这个答案。

AC自动机完整代码

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class Code_0064_AC {

    public static class Node {
        public String end;
        public boolean endUse;
        public Node fail;
        public Node[] nexts;

        public Node() {
            endUse = false;
            end = null;
            fail = null;
            nexts = new Node[26];
        }
    }

    public static class ACAutomation {
        private Node root;

        public ACAutomation() {
            root = new Node();
        }

        public void insert(String s) {
            char[] str = s.toCharArray();
            Node cur = root;
            int index = 0;
            for (char c : str) {
                index = c - 'a';
                if (cur.nexts[index] == null) {
                    Node next = new Node();
                    cur.nexts[index] = next;
                }
                cur = cur.nexts[index];
            }
            cur.end = s;
        }

        public void build() {
            Queue<Node> queue = new LinkedList<>();
            queue.add(root);
            Node cur = null;
            Node cfail = null;
            while (!queue.isEmpty()) {
                cur = queue.poll();
                for (int i = 0; i < 26; i++) {
                    if (cur.nexts[i] != null) {
                        cur.nexts[i].fail = root;
                        cfail = cur.fail;
                        while (cfail != null) {
                            if (cfail.nexts[i] != null) {
                                cur.nexts[i].fail = cfail.nexts[i];
                                break;
                            }
                            cfail = cfail.fail;
                        }
                        queue.add(cur.nexts[i]);
                    }
                }
            }
        }

        public List<String> containWords(String content) {
            char[] str = content.toCharArray();
            Node cur = root;
            Node follow;
            int path;
            List<String> ans = new ArrayList<>();
            for (char c : str) {
                path = c - 'a';
                while (cur.nexts[path] == null && cur != root) {
                    cur = cur.fail;
                }
                cur = cur.nexts[path] != null ? cur.nexts[path] : root;
                follow = cur;
                while (follow != root) {
                    if (follow.endUse) {
                        break;
                    }
                    if (follow.end != null) {
                        ans.add(follow.end);
                        follow.endUse = true;
                    }
                    follow = follow.fail;
                }
            }
            return ans;
        }

    }

    public static void main(String[] args) {
        ACAutomation ac = new ACAutomation();
        ac.insert("dhe");
        ac.insert("he");
        ac.insert("abcdheks");
        ac.insert("abdcdheks");
        ac.build();

        List<String> contains = ac.containWords("abcdhekskdjfafhasldkflskdjhwqaeruv");
        for (String word : contains) {
            System.out.println(word);
        }
    }
}

示例图

本文涉及的所有示例图见：AC自动机示例

更多

算法和数据结构学习笔记

算法和数据结构学习代码