判断两个字符串是否为扰乱字符串

判断两个字符串是否为扰乱字符串

作者：Grey

原文地址：

博客园：判断两个字符串是否为扰乱字符串

CSDN：判断两个字符串是否为扰乱字符串

题目描述

LeetCode 87. 扰乱字符串

思路

初步过滤

如果两个字符串的字符种类和数量不太一样，那么肯定不互为扰乱字符串。

暴力递归方式

f(str1,str2, L1, L2, k)

表示: str1从L1开始往后推k个长度字符，和str2从L2往后推k个长度字符，是否互为扰乱字符串

那么主函数调用：

f(str1, str2, 0, 0, str1.length) 

暴力方法中，我们枚举第一刀切str1的位置，切完第一刀后，分成的两个字符串可以旋转也可以不旋转，枚举出所有情况后，如果str2和str1互为扰动字符串，那么str2必在其中。

假设两个字符串str1和str2分别是：

str1： ABCDEFGH

str2： IJKLMNOP

假设第一刀的位置在str1的F和G之间位置

str1 就被分割成了 ABCDEF和GH两个部分

这种情况下, 如下图

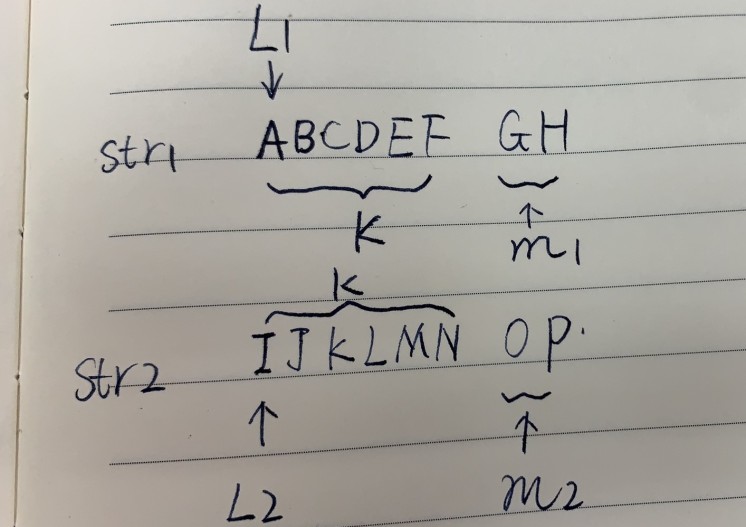
则判断两个条件：

L1往后k长度和L2往后k长度是否为扰动字符串
m1部分和m2部分是否互为扰动字符串

即：

boolean case1 = f(str1, str2, L1, L2, cutPoint) && f(str1, str2, L1 + cutPoint, L2 + cutPoint, k - cutPoint);

其中cutPoint就是str1第一刀切的位置，本例中，cutPoint即：F和G之间

还有一种情况，如下图

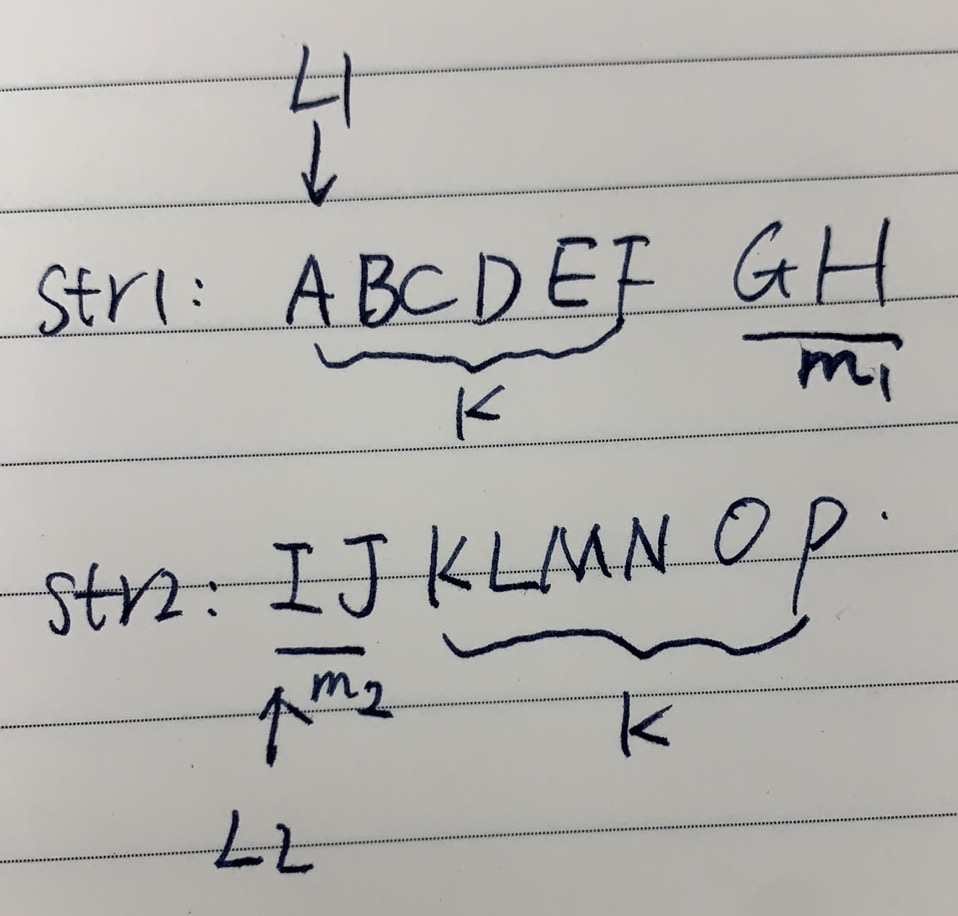
这种情况下：

boolean case2 = f(str1, str2, L1 + cutPoint, L2, k - cutPoint) && f(str1, str2, L1, L2 + k - cutPoint, cutPoint);

以上两个情况，只要一个满足，就说这两个是互为扰动串

所以，暴力方法的完整代码：

public static boolean isScramble(String s1, String s2) {
    if (s1 == null && s2 == null) {
        return true;
    }
    if (s1 == null) {
        return false;
    }
    if (s2 == null) {
        return false;
    }
    char[] str1 = s1.toCharArray();
    char[] str2 = s2.toCharArray();
    if (!isValid(str1, str2)) {
        return false;
    }
    return f(str1, str2, 0, 0, str2.length);
}

// str1中，L1往后（包括L1）一共k个字符串 以及  str2中，L2往后（包括L2）一共k个字符串 是否互为扰动串
private static boolean f(char[] str1, char[] str2, int L1, int L2, int k) {
    if (k == 1) {
        // base case， 针对这样的情况，只需要判断str1[L1], str2[L2]
        return str1[L1] == str2[L2];
    }
    // 枚举第一刀的位置
    for (int cutPoint = 1; cutPoint < k; cutPoint++) {
        boolean case1 = f(str1, str2, L1, L2, cutPoint) && f(str1, str2, L1 + cutPoint, L2 + cutPoint, k - cutPoint);
        boolean case2 = f(str1, str2, L1 + cutPoint, L2, k - cutPoint) && f(str1, str2, L1, L2 + k - cutPoint, cutPoint);
        if (case1 || case2) {
            return true;
        }
    }
    return false;
}

private static boolean isValid(char[] str1, char[] str2) {
    if (str1.length != str2.length) {
        return false;
    }
    int[] map = new int[26];
    for (char c : str1) {
        map[c - 'a']++;
    }
    for (char c : str2) {
        map[c - 'a']--;
        if (map[c - 'a'] < 0) {
            return false;
        }
    }
    return true;
}

注： isValid() 方法就是判断两个字符串的长度和字符种类个数是否一致，因为比较简单，不做赘述

这个方法在Leetcode上会超时，接下来，我们需要把这个方法改成动态规划。

记忆化搜索

由上面的暴力递归过程可知，暴力方法有三个可变参数：
L1：取值范围是[0....N-1] (其中N是字符串的长度)
L2：取值范围是[0....N-1]
k： 取值范围是[0....N]

我们可以设置一个三维数组来存暴力过程中的结果

int[][][] dp = new int[N][N][N+1]

dp[i][j][k] 的取值有三种情况：

0： 表示没有计算过
1： 表示str1中i开始推后k个字符和str2中j开始推后k个字符 是互为扰动串
-1：表示str1中i开始推后k个字符和str2中j开始推后k个字符 不是互为扰动串

把这个三维数组加入暴力递归方法中，作为缓存数据，暴力递归方法可以改成：

private static boolean f2(char[] str1, char[] str2, int L1, int L2, int k, int[][][] dp) {
    if (dp[L1][L2][k] != 0) {
        return dp[L1][L2][k] == 1;
    }
    if (k == 1) {
        // base case， 针对这样的情况，只需要判断str1[L1], str2[L2]
        dp[L1][L2][k] = (str1[L1] == str2[L2] ? 1 : -1);
        return dp[L1][L2][k] == 1;
    }
    // 枚举第一刀的位置
    boolean ans = false;
    for (int cutPoint = 1; cutPoint < k; cutPoint++) {
        boolean case1 = f2(str1, str2, L1, L2, cutPoint, dp) && f2(str1, str2, L1 + cutPoint, L2 + cutPoint, k - cutPoint, dp);
        boolean case2 = f2(str1, str2, L1 + cutPoint, L2, k - cutPoint, dp) && f2(str1, str2, L1, L2 + k - cutPoint, cutPoint, dp);
        if (case1 || case2) {
            ans = true;
            break;
        }
    }
    dp[L1][L2][k] = ans ? 1 : -1;
    return ans;
}

其中第一句逻辑：

if (dp[L1][L2][k] != 0) {
    return dp[L1][L2][k] == 1;
}

表示 dp[L1][L2][k] 如果不等于0，说明计算的结果已经算过了，则直接可以拿结果即可。

动态规划

public static boolean isScramble(String s1, String s2) {
    if (s1 == null && s2 == null) {
        return true;
    }
    if (s1 == null) {
        return false;
    }
    if (s2 == null) {
        return false;
    }
    if (s1.equals(s2)) {
        return true;
    }
    char[] str1 = s1.toCharArray();
    char[] str2 = s2.toCharArray();
    if (!isValid(str1, str2)) {
        return false;
    }
    int N = str1.length;
    boolean[][][] dp = new boolean[N][N][N + 1];
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            dp[i][j][1] = (str1[i] == str2[j]);
        }
    }

    for (int k = 2; k < N + 1; k++) {
        for (int L1 = 0; L1 <= N - k; L1++) {
            for (int L2 = 0; L2 <= N - k; L2++) {
                for (int cutPoint = 1; cutPoint < k; cutPoint++) {
                    boolean case1 = dp[L1][L2][cutPoint] && dp[L1 + cutPoint][L2 + cutPoint][k - cutPoint];
                    boolean case2 = dp[L1 + cutPoint][L2][k - cutPoint] && dp[L1][L2 + k - cutPoint][cutPoint];
                    if (case1 || case2) {
                        dp[L1][L2][k] = true;
                        break;
                    }
                }
            }
        }
    }
    return dp[0][0][N];
}

更多

算法和数据结构笔记