万仓一黍

摘要： 1、1、2、3、5、8、13、21、……。这个数列称为斐波那契数列（Fibonacci Sequence）。它有个奇妙的性质，记FN为斐波那契数列的第N项，则当N比较大的时候FN/FN+1≈0.618斐波那契数列有两个常见的通项公式（具体的推导过程就忽略了）1、FN=FN-1+FN-2（N>2），F1=1，F2=22、这个数列的前两项F1=1，F2=1才称为斐波那契数列，如果这个数列的前两项是其他数字（正数），并且还有FN=FN-1+FN-2（N>2）的递推关系，那么这样的数列，我称之为类斐波那契数列，它是否还有当N比较大的时候，FN/FN+1≈0.618这个奇妙的性质呢？答案是肯 阅读全文

摘要： 之前发了一篇博文“24点的所有组合的解法”，有人颇不以为然。我想说的是，发这篇文章是说明我可以用计算机求出24点的所有组合的解法。而在实际的运用中，如果要使用24点的算法有时还不见得利用查表法来得简单和快速。毕竟，要短时间内写出正确的算法并验证，也不是一件很容易的事。24点游戏的规则：给定4个正整数（1到10），利用加减乘除运算，得出运算结果为24的运算式例如：1，2，3，4——（1+2+3）*4=241，5，5，5——（5-1/5）*5=24网上比较常见的24点算法是动态规划算法（这个在博客园中也能搜索到）。定义6个二元运算符：加、减、乘、除、反减、反除然后从4个数中任选2个数，通过一种运算 阅读全文

摘要： 为这个设计师击节叫好，巧妙的运用色彩实现了3D效果。该设计师运用色彩和PS技巧随心所欲，苦了翻译的人，在没有源文件的情况下，对某些步骤还得推敲一番，好在有之前翻译的教程中的经验在，有些步骤还是能复原的，或者是近似的去实现它。 阅读全文

摘要： 这是一篇写在它处的老文章了。近日翻翻，颇有意思。于是在此再次发布。研究24点的算法。觉得穷举法是一种可以接受的解法。利用时下的计算机。就是穷举从1，1，1，1到10，10，10，10的所有数字组合的解法也不过就几秒钟而已。而且，可以将所有的结果保存在文件里，以供日后其他应用时方便调用，加快计算速度。下面将有结果的组合和解法赋予其后，有兴趣的同道之人可以参阅。1,1,1,8 －－－ 8×(1＋1＋1)=241,1,2,6 －－－ 2×6×(1＋1)=241,1,2,7 －－－ (1＋2)×(7＋1)=241,1,2,8 －－－ (1＋2)×8&# 阅读全文

摘要： 之前一段时间，翻译了一些国外的PS网页设计教程，这些教程中都有一些共性，例如包含网页LOGO、导航菜单栏、图片滑动栏、版权信息等。其中在多个教程中都提到了利用JQuery插件实现图片滑动栏。于是在网上搜索了一番，发现类似的插件千千万万，都有各自的特色。故本教程挑选了其中的一个插件，进行讲解，并在后面结合实例讲解如何在PS中切片，在导出的网页中完成图片滑动栏栏的制作。插件网址：http://slidesjs.com/插件示例网址：http://slidesjs.com/examples/standard/插件的参数：preload (boolean)设置为true时，显示一个预加载图像。在图片比 阅读全文

摘要： 本教程被誉为2012年的推荐教程。整个页面简洁干净。本教程主要技术有：1、圆角六边形的制作。充分利用描边效果来完成圆角六边形的制作。2、用自定义的简单图案实现各种各样的纹理，其效果像是铜版纸的效果。1、巧妙的利用图层的叠加实现特殊的外发光的效果。 阅读全文

摘要： 近日，在网上闲逛的时候。发现一篇不错的3D点阵字的教程。在自己亲历实为后，将教程赋予下方。本教程不是原创，在原创的基础上，做了适当的改良。完成的作品如下：步骤1：建立参考模版新建20px*20px的文档，放大为800%，用文字工具书写文字“朱”，边缘选项选择无这个作为后面步骤的模版步骤2：创建基本方块不要关闭之前的文档，新建文档500px*500px。用矩形工具创建一个矩形，尺寸：19px*19px，颜色： #0a6b8e按Ctrl + J复制图层，并移动到原图层上方19px处，颜色改为： #2bb3e5再次复制图层，并移动到原图层左侧19px处，颜色改为： #208ab1对上方的矩形，向左倾 阅读全文

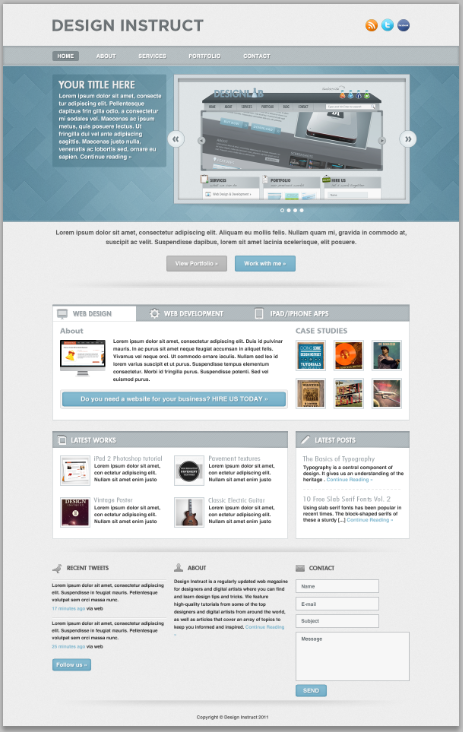摘要： 本教程是非常详细的教程。特色主要有两点，一是斜纹图案的制作，二是选项卡的制作，这在其他的教程中不常见的 阅读全文

摘要： 这是一篇风格迥异的教程。该教程中的这几个方面是个特色：一是风轮效果，原教程中是用网上下载的画刷，我改成自己制作；二是独特的图案叠加效果；三是有趣的糖遮效果 阅读全文

摘要： 问题的描述：现在有N个一模一样的苹果，要放在编号为1、2、3……、N的盘子里（假设盘子足够大，能放下所有的苹果），问一共有多少种放法？ 算法分析： 用符号F（i，j）表示i个苹果放在j个盘子里的放法数 如果1号盘子里没有苹果，则i个苹果要放在剩余的j-1个盘子里 如果1号盘里有1个苹果，则剩余的i-1个苹果放在剩余的j-1个盘子里 如果1号盘里有2个苹果，则剩余的i-2个苹果放在剩余的j-1个盘子里 以此类推 如果1号盘里有i-1个苹果，则剩下的1个苹果放在j-1个盘子里 如果1号盘里有i个苹果，则剩下的j-1个盘子里没有苹果 于是得到以下的关系式 ① F（i，j）... 阅读全文