【笔记】 卷积

题目

• HDU 4609 3-idiots
  题目链接
  题解
  这个题考察了如何转化成多项式乘法，然后去重和计数很有意思
• HDU 1402 A*B problem plus
  题目链接
  将整数转化成向量，最后得到的卷积后的向量处理一下每一位的进位就是结果
• BZOJ 2194 快速傅立叶之二
  题目链接
  FFT 能解决形如 c[k] =sigma(a[p]*b[k-p]) (0<=p<=k) 的式子，如果是c[k] = sigma(a[p],b[p+k]),可以将其中一个向量倒过来，这样就变成第一种情况了，当然所求的下标也变化了
• BZOJ 3527 力
  题目链接
  公式推导
  和BZOJ2194类似，我们要将原式转化成c[k] =sigma(a[p]*b[k-p]) (0<=p<=k) ， 熟练运用换元法、缩放和向量转置，得到满足卷积条件的表达式
• BZOJ 3771 Triple
  题目链接
  容斥分析
  这道题考点在于是否了解DFT、IDFT之后求的是什么东西，只要心里清楚，就很容易做了

什么是卷积

参考资料1
参考资料2

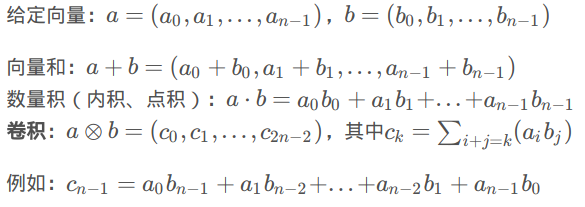
多项式乘法就是求卷积
1 3 3 4
把这个数组转化成num数组，num[i]表示数字i的有num[i]个。
num = {0 1 0 2 1}
代表0的有0个，1有1个，2有0个，3有2个，4有1个。
使用FFT解决的问题就是num数组和num数组卷积。
num数组和num数组卷积的解决，其实就是从{1 3 3 4}取一个数，从{1 3 3 4}再取一个数，他们的和每个值各有多少个
例如：
{0 1 0 2 1}{0 1 0 2 1} 卷积的结果应该是{0 0 1 0 4 2 4 4 1 }
长度为n的数组和长度为m的数组卷积，结果是长度为n+m-1的数组。
{0 1 0 2 1} 卷积的结果应该是{0 0 1 0 4 2 4 4 1 }。
这个结果的意义如下：
从{1 3 3 4}取一个数，从{1 3 3 4}再取一个数
取两个数和为 2 的取法是一种：1+1
和为 4 的取法有四种：1+3， 1+3 ，3+1 ，3+1
和为 5 的取法有两种：1+4 ，4+1；
和为 6的取法有四种：3+3,3+3,3+3,3+3,3+3
和为 7 的取法有四种： 3+4,3+4,4+3,4+3
和为 8 的取法有 一种：4+4

关于多项式

• 次数界：对于多项式A(x)，系数为ai,设最高非零系数为ak，任何大于k的整数都是A(x)的次数界
• 系数表达式：
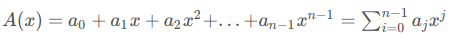
• 系数向量：a=(a0,a1,...,an−1)
• 点值表达方式：{(x0,y0),(x1,y1),...,(xn−1,yn−1)} ，其中xk各不相同，yk=A(xk)

快速傅立叶变换（FFT）

快速计算DFT（离散傅里叶变换）的算法
时间复杂度：O(nlogn)

复数

const double pi = acos(-1);
const double pi_2 = 2*pi;
struct Complex // 复数
{
    double r, i;
    Complex(double _r = 0, double _i = 0) :r(_r), i(_i) {}
    Complex operator +(const Complex &b) {
        return Complex(r + b.r, i + b.i);
    }
    Complex operator -(const Complex &b) {
        return Complex(r - b.r, i - b.i);
    }
    Complex operator *(const Complex &b) {
        return Complex(r*b.r - i*b.i, r*b.i + i*b.r);
    }
};

FFT模板

• 非递归

void func1(Complex pos[],int n){
    int j = __builtin_ctz(n)-1;
    for(int i=0;i<n;i++) pos[i] = pos[i>>1]>>1 | ((i&1)<<j);
}
void fft(Complex y[],int len,int on){
    change(y,len);
    for(int h=2;h<=len;h<<=1){
        Complex wn(cos(-on*pi_2/h),sin(-on*pi_2/h));
        for(int j=0;j<len;j+=h){
            Complex w(1,0);
            for(int k=j;k<j+h/2;++k){
                Complex u=y[k],t=w*y[k+h/2];
                y[k]=u+t;
                y[k+h/2]=u-t;
                w=w*wn;
            }
        }
    }
    if(on==-1)
    for(int i=0;i<len;++i)
    y[i].r/=len;
}

步骤

• 补0
  在两个多项式前面补0，得到两个2n次多项式，设系数向量分别为v1和v2。
• 求值
  使用FFT计算f1=DFT(v1)和f2=DFT(v2)。则f1与f2为两个多项式在2n次单位根处的取值（即点值表示）。
• 乘法
  把f1与f2每一维对应相乘，得到f，代表对应输入多项式乘积的点值表示。
• 插值
  使用IFFT计算v=IDFT(f)，其中v就是乘积的系数向量。

while(len < len1*2) len<<=1;
for(int i = 0;i<len1;i++)
	x1[i] = Complex(num[i],0);
for(int i = len1;i<len;i++)
	x1[i] = Complex(0,0);
fft(x1,len,1);
for(int i = 0;i<len;i++)
	x1[i]= x1[i]*x1[i];
fft(x1,len,-1);
for(int i = 0;i<len;i++)
	num[i] = (long long)(x1[i].r+0.5);

快速数论变换（NTT）

当FFT需要取模P且Ｐ存在原根时，就能用NTT来求卷积
原根的知识见离散对数
NTT用到的部分素数及原根
如果不在表中可以自行计算

const int N = 1000;
bool not_prime[N+5];
int prime[N+5],tot_prime,pr[N+5],tot_pr;
int g;
void sss(){ 
    for(int i=2;i<N;i++){
    if(!not_prime[i]) prime[++tot_prime]=i;
    for(int j=1;j<=tot_prime;j++){
        int t = i*prime[j];if(t>=N) break;not_prime[t]=true;
        if(i%prime[j]==0)break;
    }
    }
}
void get(int p){    int temp=p-1;
    for(int i=1;i<=tot_prime&&prime[i]*prime[i]<=temp;i++)
    if(temp%prime[i]==0){
        while(temp%prime[i]==0) temp /= prime[i];
        pr[++tot_pr] = prime[i];
    }
    if(temp>1) pr[++tot_pr]=temp;
}
bool check(int d,int p){ 
    if (__gcd(d,p)!=1)return 0;
    for(int i=1;i<=tot_pr;i++)if(qpow(d,(p-1)/pr[i])==1)return 0;
    return 1; 
}
int get_g(int p) {
    int g=1;
    sss();get(p);
    for(int i=2;i<p;i++) if(check(i,p)) {g=i;break;}
    return g;
}

ntt的接口使用和fft 类似，长度一定是２的幂次倍

int rev(int x,int r) {
    int ans=0;
    for(int i=0;i<r;i++) if(x&(1<<i)) ans+=1<<(r-i-1);
    return ans;
}
void ntt(int n,ll a[],int on) {
    int r = 0;
    while((1<<r)<n) r++;
    for(int i=0;i<n;i++) {
        int tmp = rev(i,r);
        if(i < tmp)  swap(a[i],a[tmp]);
    }
    for(int s=1;s<=r;s++) {
        int m = 1<<s;
        ll wn=qpow(g,(mod-1)/m);
        for(int k=0;k<n;k+=m){
            ll w=1;
            for(int j=0;j<(m>>1);j++) {
                ll t = w * a[k+j+(m>>1)] % mod;
                ll u=a[k+j];
                a[k+j] = (u+t)%mod;
                a[k+j+(m>>1)] = (u-t)%mod;if(a[k+j+(m>>1)]<0)a[k+j+(m>>1)]+=mod;
                w = w*wn%mod;
            }
        }
    }
    if(on==-1) {
        for(int i=1;i<(n>>1);i++) swap(a[i],a[n-i]);
        ll inv = qpow(n,mod-2);
        for(int i=0;i<n;i++) a[i] = a[i] * inv % mod;
    }
}