动手实现深度学习(9):第四篇:optimization的实现
传送门: https://www.cnblogs.com/greentomlee/p/12314064.html
github: Leezhen2014: https://github.com/Leezhen2014/python_deep_learning
六 optimization的实现
神经网络的学习目的是找到使得损失函数的值尽可能小的参数,这个寻找最优参数的过程称为最优化(optimization)。本章会介绍4中优化函数,给出实现代码和测例。
测例方面,首先会用函数做测试,观察是否可以逼近极小值;然后会用mnist数据集做测试观察是否能够收敛。
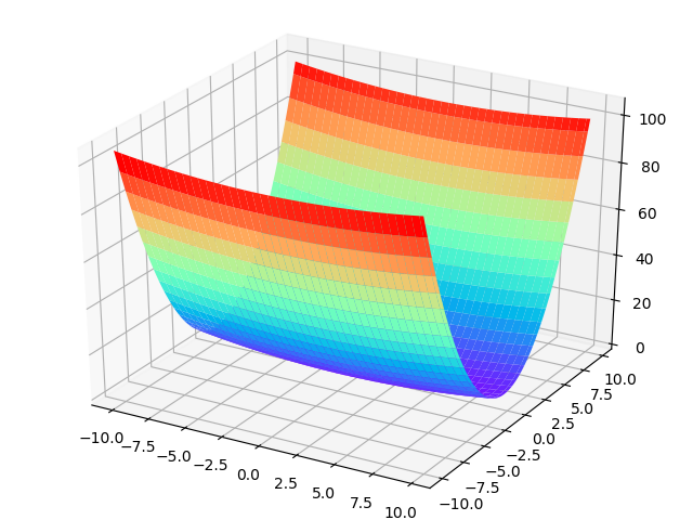
所测试的函数公式如下:
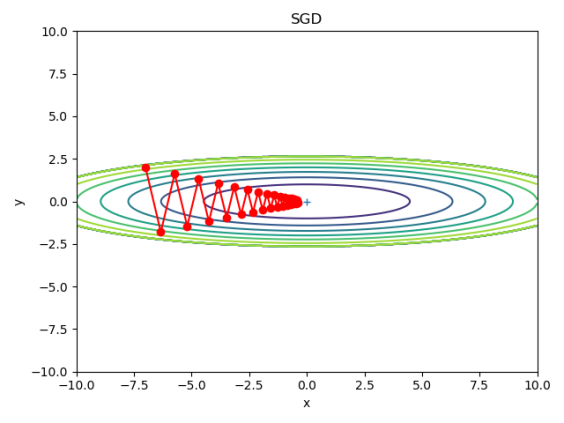
6.1 随机梯度下降(stochastic gradient descent, SGD)的实现
在前几篇两篇中一直使用同一种的方法修改权重。这种方法为了寻找最优参数,将参数的梯度(导数)作为依据,根据参数的梯度,就知道梯度的方向,并沿着梯度的方向更新参数。通过不断的更新迭代上述步骤,从而逐渐接近最优参数。这个过程称为随机梯度下降(stochastic gradient descent, SGD),前面几篇的训练中一直使用的是SGD。SGD的数学表达式如下:
虽然实现简单,也能得到优化参数。但是SGD有很多缺点, 比较明显的一个就是梯度的方向并没有指向最小值的方向,有可能得到的最优解是局部最优解。
因此我们还应该实现其他的优化参数的方法。 不过在此之前,需要对程序做修改,之前代码的耦合性很高,先把SGD独立抽出来,写成一个class,代码如下。
1 class SGD: 2 3 """梯度下降(Stochastic Gradient Descent)""" 4 5 def __init__(self, lr=0.01): 6 self.lr = lr 7 8 def update(self, params, grads): 9 for key in params.keys(): 10 params[key] -= self.lr * grads[key]
PS: 2/3里面均是采用SGD寻找最优参数,我们也可以从代码中找到,优化代码结构。
在第3篇的mnist数据集训练手写体:
1 def gradient(self, x, t): 2 # forward 3 dout=self.loss(x, t) 4 5 # backward 6 # dout = 1 7 dout = self.lastLayer.backward(dout) 8 9 layers = list(self.layers.values()) 10 layers.reverse() 11 for layer in layers: 12 dout = layer.backward(dout) 13 14 # 更新 15 grads = {} 16 grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db 17 grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db 18 19 return grads
第二篇里的2.4节,mnist数据集训练手写体:
1 def gradient(self, x, t): 2 W1, W2 = self.params['W1'], self.params['W2'] 3 b1, b2 = self.params['b1'], self.params['b2'] 4 grads = {} 5 6 batch_num = x.shape[0] 7 8 # forward 9 a1 = np.dot(x, W1) + b1 10 z1 = sigmoid(a1) 11 a2 = np.dot(z1, W2) + b2 12 y = softmax(a2) 13 14 # backward 15 dy = (y - t) / batch_num 16 grads['W2'] = np.dot(z1.T, dy) 17 grads['b2'] = np.sum(dy, axis=0) 18 19 dz1 = np.dot(dy, W2.T) 20 da1 = sigmoid_grad(a1) * dz1 21 grads['W1'] = np.dot(x.T, da1) 22 grads['b1'] = np.sum(da1, axis=0) 23 24 return grads
测试SGD:
与之前测试梯度的方法类似:给出一个函数公式,求它的梯度。但这次会将每次梯度下降的点绘制出来。
1 # coding: utf-8 2 import numpy as np 3 4 import matplotlib.pyplot as plt 5 from collections import OrderedDict 6 from src.common.optimizer import * 7 8 9 def f(x, y): 10 return x**2 / 20.0 + y**2 11 12 13 def df(x, y): 14 return x / 10.0, 2.0*y 15 16 init_pos = (-7.0, 2.0) 17 params = {} 18 params['x'], params['y'] = init_pos[0], init_pos[1] 19 grads = {} 20 grads['x'], grads['y'] = 0, 0 21 22 23 optimizer= SGD(lr=0.95) 24 # optimizer=Momentum(lr=0.1) 25 # optimizer=AdaGrad(lr=1.5) 26 # optimizer= Adam(lr=0.3) 27 # optimizer=RMSprop() 28 29 30 31 x_history = [] 32 y_history = [] 33 params['x'], params['y'] = init_pos[0], init_pos[1] 34 35 for i in range(30): 36 x_history.append(params['x']) 37 y_history.append(params['y']) 38 39 grads['x'], grads['y'] = df(params['x'], params['y']) 40 optimizer.update(params, grads) 41 42 43 x = np.arange(-10, 10, 0.01) 44 y = np.arange(-5, 5, 0.01) 45 46 X, Y = np.meshgrid(x, y) 47 Z = f(X, Y) 48 49 mask = Z > 7 50 Z[mask] = 0 51 52 plt.plot(x_history, y_history, 'o-', color="red") 53 plt.contour(X, Y, Z) 54 plt.ylim(-10, 10) 55 plt.xlim(-10, 10) 56 plt.plot(0, 0, '+') 57 # colorbar() 58 # spring() 59 plt.title("Momentum") 60 plt.xlabel("x") 61 plt.ylabel("y") 62 63 plt.show()
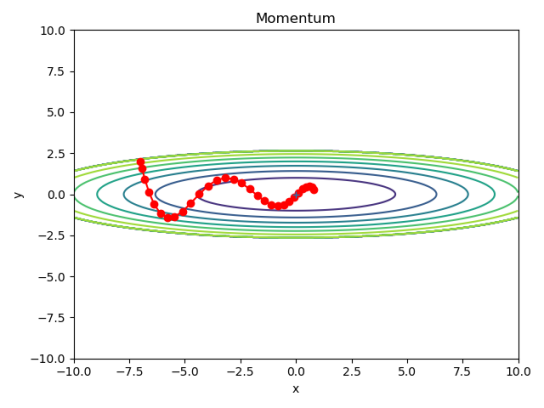
6.2 Momentum的实现
针对SGD的缺点,添加动量v,对应物理上的速度。这样公式类似于物理上的瞬时速度的公式,![]() 对应物理上的阻力。
对应物理上的阻力。
1 class Momentum: 2 3 """添加动量后的 SGD""" 4 5 def __init__(self, lr=0.01, momentum=0.9): 6 self.lr = lr 7 self.momentum = momentum 8 self.v = None 9 10 def update(self, params, grads): 11 if self.v is None: 12 self.v = {} 13 for key, val in params.items(): 14 self.v[key] = np.zeros_like(val) 15 16 for key in params.keys(): 17 self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 18 params[key] += self.v[key]
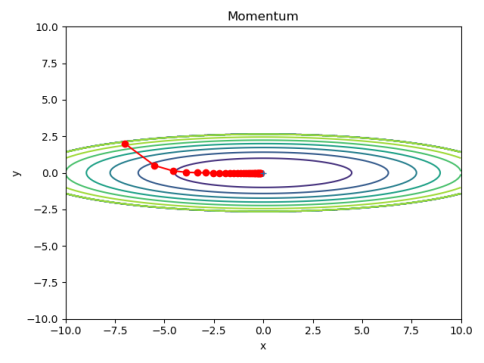
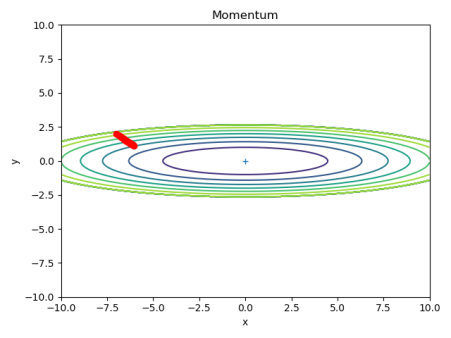
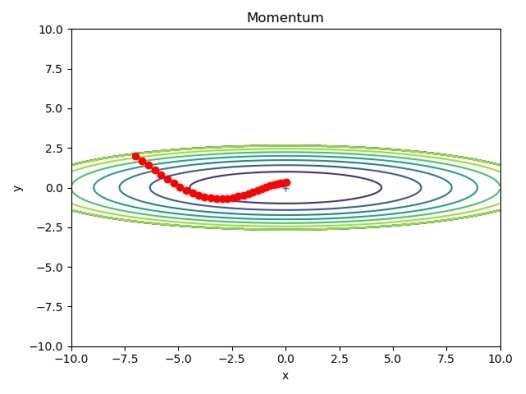
代码测试:
参考资料:
https://tensorflow.google.cn/api_docs/cc/class/tensorflow/ops/apply-momentum?hl=en
6.3 AdaGrad
AdaGrad又称为学习率衰减。在神经网络的训练过程中,学习率的设置很重要,如果学习设置过小,导致学习的时间很长;学习率过大导致不能收敛。
针对以上的这种情况,有人提出了learning rate decay的方法:可以让学习率一开始比较大,随着训练的次数增加,学习率不断减少。AdaGrad(Adaptive Grad)会对每个元素的学习率进行适当的调整。AdaGrad的数学表达式如下:
由于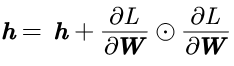 保存了以前所有梯度值的平方和,所以在更新参数的时候需要对除以
保存了以前所有梯度值的平方和,所以在更新参数的时候需要对除以![]() 才可以。这样一来,参数元素中变动较大的元素的学习率会降低。可以看做按照参数的元素进行学习率的衰减,使得变动较大的参数的学习率减小。
才可以。这样一来,参数元素中变动较大的元素的学习率会降低。可以看做按照参数的元素进行学习率的衰减,使得变动较大的参数的学习率减小。
AdaGrad会记录所有梯度的平方和,然后在减去对应的梯度的权重,因此学习越深入,更新的幅度会越小。
1 class AdaGrad: 2 3 """AdaGrad的实现""" 4 5 def __init__(self, lr=0.01): 6 self.lr = lr 7 self.h = None 8 9 def update(self, params, grads): 10 if self.h is None: 11 self.h = {} 12 for key, val in params.items(): 13 self.h[key] = np.zeros_like(val) 14 15 for key in params.keys(): 16 self.h[key] += grads[key] * grads[key] """求平方和,平方和中包含了每个元素 """ 17 params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
测试代码:
参考资料:
https://tensorflow.google.cn/api_docs/python/tf/keras/optimizers/Adagrad?hl=en
https://tensorflow.google.cn/api_docs/cc/class/tensorflow/ops/apply-adagrad?hl=en
6.5 RMSProp的实现
从公式上看AdaGrad会迭代更新权重,这意味着会记录过去所有的平方和。可能会存在学习越深入更新的幅度会越小,甚至到最后几乎为0的情况。从上图可以看出确实出现了这种情况。
RMSProp可以改善这种情况。
RMSProp不是将过去的所有梯度都一视同仁的相加,而是逐渐的遗忘过去的梯度。
这里的代码实现就不给出了;, 具体可以从github上获取:
6.4 adam的实现
这里给出一个博客园大佬对adam的介绍和说明, 我就没有必要再赘述了: https://www.cnblogs.com/yifdu25/p/8183587.html
Adam的思路是将adaGrad和momnentum结合在一起。论文中Adam会设置3个参数:学习率![]() ,一次动量系数
,一次动量系数![]() ,二次动量系数
,二次动量系数![]() 。
。
1 class Adam: 2 3 """ 4 Adam (http://arxiv.org/abs/1412.6980v8) 5 """ 6 7 def __init__(self, lr=0.001, beta1=0.9, beta2=0.999): 8 self.lr = lr 9 self.beta1 = beta1 10 self.beta2 = beta2 11 self.iter = 0 12 self.m = None 13 self.v = None 14 15 def update(self, params, grads): 16 if self.m is None: 17 self.m, self.v = {}, {} 18 for key, val in params.items(): 19 self.m[key] = np.zeros_like(val) 20 self.v[key] = np.zeros_like(val) 21 22 self.iter += 1 23 lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter) 24 25 for key in params.keys(): 26 #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key] 27 #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2) 28 self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key]) 29 self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key]) 30 31 params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
测试代码:
参考资料:
https://tensorflow.google.cn/api_docs/python/tf/keras/optimizers/Adam?hl=en
6.5 构造神经网络
1 # -*- coding: utf-8 -*- 2 # @File : multi_layer.py 3 # @Author: lizhen 4 # @Date : 2020/2/4 5 # @Desc : 多层神经网络 6 7 import numpy as np 8 from collections import OrderedDict 9 from src.common.layers import Sigmoid,Relu,Affine,SoftmaxWithLoss 10 from src.common.gradient import numerical_gradient 11 12 13 class MultiLayerNet: 14 15 def __init__(self, input_size, hidden_size_list, output_size, 16 activation='relu', weight_init_std='relu', weight_decay_lambda=0): 17 ''' 18 全连接的神经网络 19 :param input_size: 输入大小,784 20 :param hidden_size_list: 隐含层的大小(e.g. [100, 100, 100]) 21 :param output_size: 输出层的大小,10 22 :param activation: 激活函数 'relu' or 'sigmoid' 23 :param weight_init_std: 数据做标准化(e.g. 0.01) 24 :param weight_decay_lambda: 权值衰减系数 25 ''' 26 self.input_size = input_size 27 self.output_size = output_size 28 self.hidden_size_list = hidden_size_list 29 self.hidden_layer_num = len(hidden_size_list) 30 self.weight_decay_lambda = weight_decay_lambda 31 self.params = {} 32 33 # 初始化权重 34 self.__init_weight(weight_init_std) 35 36 # 激活层 37 activation_layer = {'sigmoid': Sigmoid, 'relu': Relu} 38 self.layers = OrderedDict() 39 for idx in range(1, self.hidden_layer_num+1): 40 self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], 41 self.params['b' + str(idx)]) 42 self.layers['Activation_function' + str(idx)] = activation_layer[activation]() 43 44 idx = self.hidden_layer_num + 1 45 self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], 46 self.params['b' + str(idx)]) 47 48 self.last_layer = SoftmaxWithLoss() 49 50 def __init_weight(self, weight_init_std): 51 """ 52 初始化权重 53 :param weight_init_std: 指定权重使用的标准差,{'relu','He','Sigmoid','xavier'} 54 weight_init_std 可以使用的输入 55 :return: 56 """ 57 58 all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size] 59 for idx in range(1, len(all_size_list)): 60 scale = weight_init_std 61 if str(weight_init_std).lower() in ('relu', 'he'):# 使用relu的情况 62 scale = np.sqrt(2.0 / all_size_list[idx - 1]) 63 elif str(weight_init_std).lower() in ('sigmoid', 'xavier'): 64 scale = np.sqrt(1.0 / all_size_list[idx - 1]) # 使用sigmoid的情况 65 66 self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx]) 67 self.params['b' + str(idx)] = np.zeros(all_size_list[idx]) 68 69 def predict(self, x): 70 for layer in self.layers.values(): 71 x = layer.forward(x) 72 73 return x 74 75 def loss(self, x, t): 76 """ 77 损失函数 78 :param x: 输入数据 79 :param t: 标签数据 80 :return: 损失值 81 """ 82 83 y = self.predict(x) 84 85 weight_decay = 0 86 for idx in range(1, self.hidden_layer_num + 2): 87 W = self.params['W' + str(idx)] 88 weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2) 89 90 return self.last_layer.forward(y, t) + weight_decay 91 92 def accuracy(self, x, t): 93 y = self.predict(x) 94 y = np.argmax(y, axis=1) 95 if t.ndim != 1 : t = np.argmax(t, axis=1) 96 97 accuracy = np.sum(y == t) / float(x.shape[0]) 98 return accuracy 99 100 def numerical_gradient(self, x, t): 101 ''' 102 求数值微分 103 :param x: 输入的数据 104 :param t: 标签数据 105 :return: 返回每一层的梯度 106 ''' 107 108 loss_W = lambda W: self.loss(x, t) 109 110 grads = {} 111 for idx in range(1, self.hidden_layer_num+2): 112 grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)]) 113 grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)]) 114 115 return grads 116 117 def gradient(self, x, t): 118 ''' 119 寻找每层的梯度 120 :param x: 输入数据 121 :param t: 标签 122 :return:返回每层的梯度变量 123 ''' 124 # forward 125 self.loss(x, t) 126 127 # backward 128 dout = 1 129 dout = self.last_layer.backward(dout) 130 131 layers = list(self.layers.values()) 132 layers.reverse() 133 for layer in layers: 134 dout = layer.backward(dout) 135 136 137 grads = {} 138 for idx in range(1, self.hidden_layer_num+2): 139 grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W 140 grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db 141 142 return grads
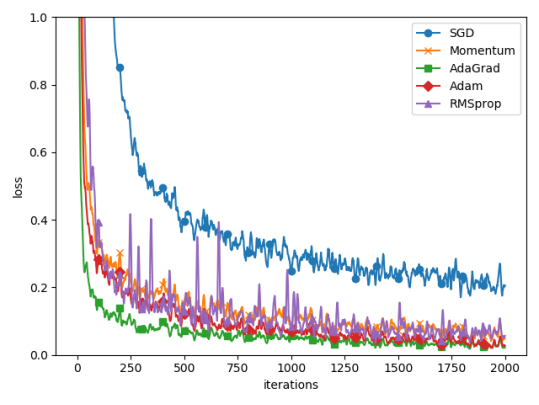
6.6 opt的对比(基于mnist数据集)
P.S:这里面把RMSprop也放进来做参考了。
1 2 # coding: utf-8 3 # opt的对比(基于mnist数据集) 4 5 import matplotlib.pyplot as plt 6 from src.datasets.mnist import load_mnist 7 from src.common.util import smooth_curve 8 from src.common.multi_layer_net import MultiLayerNet 9 from src.common.optimizer import * 10 11 12 # 0:MNIST数据集 13 (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True) 14 15 train_size = x_train.shape[0] 16 batch_size = 128 17 max_iterations = 2000 18 19 20 # 1:设置优化器 21 optimizers = {} 22 optimizers['SGD'] = SGD() 23 optimizers['Momentum'] = Momentum() 24 optimizers['AdaGrad'] = AdaGrad() 25 optimizers['Adam'] = Adam() 26 optimizers['RMSprop'] = RMSprop() 27 28 networks = {} 29 train_loss = {} 30 for key in optimizers.keys(): 31 networks[key] = MultiLayerNet( 32 input_size=784, hidden_size_list=[100, 100, 100, 100], 33 output_size=10) 34 train_loss[key] = [] 35 36 37 # 2:训练: 38 for i in range(max_iterations): 39 batch_mask = np.random.choice(train_size, batch_size) 40 x_batch = x_train[batch_mask] 41 t_batch = t_train[batch_mask] 42 43 for key in optimizers.keys(): 44 grads = networks[key].gradient(x_batch, t_batch) 45 optimizers[key].update(networks[key].params, grads) 46 47 loss = networks[key].loss(x_batch, t_batch) 48 train_loss[key].append(loss) 49 50 if i % 100 == 0: 51 print( "===========" + "iteration:" + str(i) + "===========") 52 for key in optimizers.keys(): 53 loss = networks[key].loss(x_batch, t_batch) 54 print(key + ":" + str(loss)) 55 56 57 # 3.绘图 58 markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D","RMSprop":"^"} 59 x = np.arange(max_iterations) 60 for key in optimizers.keys(): 61 plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key) 62 plt.xlabel("iterations") 63 plt.ylabel("loss") 64 plt.ylim(0, 1) 65 plt.legend() 66 plt.show() 67
4.6 总结
在网上找到了一些资料:



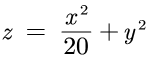
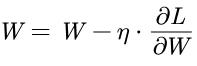
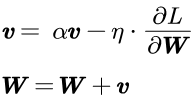
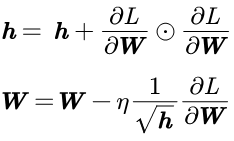
![wps53[4] wps53[4]](https://img2022.cnblogs.com/blog/529380/202209/529380-20220912175015067-372269287.png)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号