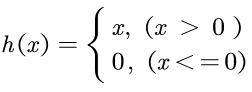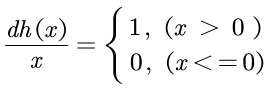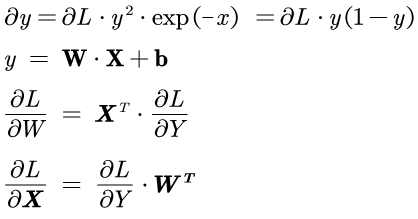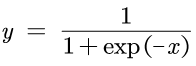动手实现深度学习（6）：实现基于计算图的激活层

传送门： https://www.cnblogs.com/greentomlee/p/12314064.html

github: Leezhen2014: https://github.com/Leezhen2014/python_deep_learning

 

在第二篇中介绍了用数值微分的形式计算神经网络的梯度，数值微分的形式比较简单也容易实现，但是计算上比较耗时。本章会介绍一种能够较为高效的计算出梯度的方法：基于图的误差反向传播。

根据 deep learning from scratch 这本书的介绍，在误差反向传播方法的实现上有两种方法：一种是基于数学式的（第二篇就是利用的这种方法），一种是基于计算图的。这两种方法的本质是一样的，有所不同的是表述方法。计算图的方法可以参考feifei li负责的斯坦福大学公开课CS231n 或者theano的tutorial/Futher readings/graph Structures.

之前我们的误差传播是基于数学式的，可以看出对代码编写者来说很麻烦；

这次我们换成基于计算图的；

5.2 激活层的实现

本节的函数是基于 第二篇：2. 激活函数的设计与实现

由于需要将计算图的思路用在神经网络中，所以需要把之前实现的激活函数重新实现一次。

 

 

5.2.1 ReLU层

Relu的backward 是relu函数的微分。

微分的计算如下：

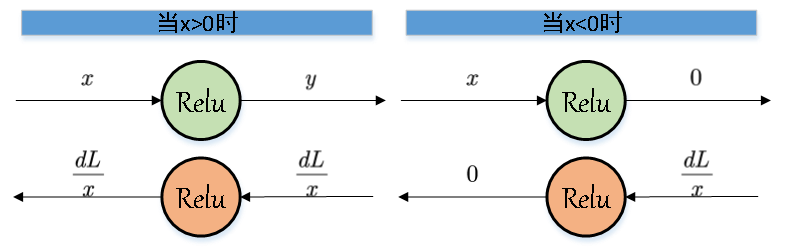
其计算图的表示如下：

可见当x<0的时候，在backward部分应该输出0, 其余的情况输出的是微分。

Backward中的dout变量表示的是dL

用使用公式求微分，和使用计算图求微分的结果是一样的。

实现代码：

class Relu:

    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 1

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

 

5.2.2 Sigmoid层

微分的公式为：

Backward中的dout变量表示的是dL，

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx