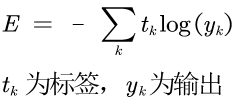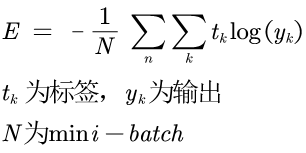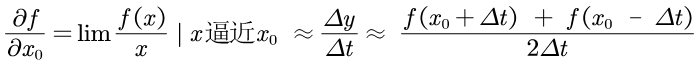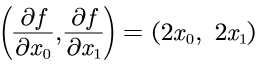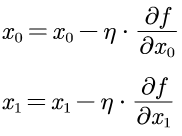动手实现深度学习(4): 神经网络的backward实现

传送门： https://www.cnblogs.com/greentomlee/p/12314064.html

github: https://github.com/Leezhen2014/python_deep_learning

 

在第二篇中介绍了用数值微分的形式计算神经网络的梯度，数值微分的形式比较简单也容易实现，但是计算上比较耗时。本章会介绍一种能够较为高效的计算出梯度的方法：基于图的误差反向传播。

根据 deep learning from scratch 这本书的介绍，在误差反向传播方法的实现上有两种方法：一种是基于数学式的（第二篇就是利用的这种方法），一种是基于计算图的。这两种方法的本质是一样的，有所不同的是表述方法。计算图的方法可以参考feifei li负责的斯坦福大学公开课CS231n 或者theano的tutorial/Futher readings/graph Structures.

之前我们的误差传播是基于数学式的，可以看出对代码编写者来说很麻烦；

这次我们换成基于计算图的；

Backward是神经网络训练过程中包含的一个过程，在这个过程中会通过反馈调节网络中各个节点的权重，以此达到最佳权重参数。在反馈中，loss value是起点，是衡量与label之间差距的值。Loss value 自然是loss function计算得出的。

TODO:

本章会讲解常见的两种loss function

然后会介绍梯度，梯度是用于修改节点权重的。

最后会实现backward，用mnist数据集训练;

 

 

4.1 损失函数

损失函数的种类有很多， 本案只介绍两种损失函数： 均方差、交叉熵；

然后会将交叉熵改写成n-batch的交叉熵；

均方误差（mean squared error）

实现如下：

def mean_squared_error(y, t):
    return 0.5*np.sum((y-t)**2)

 

交叉熵误差（cross entropy error）

交叉熵的公式和实现如下：

def cross_entropy_error(y,t):
    delta = 1e-7
    return -np.sum(t*np.log(y+delta))

 

 

mini-batch版本的损失函数

上述的两个损失函数都是针对于1-batch做的损失函数；如果输入的数据是n-batch的话，上述的损失函数不太适用了；

需要对损失函数做一下修改，以交叉熵为例，n-batch的交叉熵公式和代码实现如下：

 

def cross_entropy_error(y,t):
# batch版本的交叉熵
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0] # batch

    delta = 1e-7
    return -np.sum(t*np.log(y+delta))/batch_size

 

4.2 梯度

本节介绍梯度法的实现，不涉及神经网络的反馈算法。本节内容是为下一节反馈算法做铺垫。

神经网络学习的本质是根据数据的label和预测值的误差，即loss value，然后根据误差修改权重信息。

数据的label和预测值的误差可以使用损失函数来衡量，获得loss value。

修改权重的信息可以用求数学统计求极值的方式获得。

 

已知导数为0的点为极值点，可以通过求导数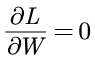一次性找到极值点。但是这种方法在数据样本或者W的规模相当大的情况下是无法计算的，在具有多个变量的情况下会计算多次的偏导数，可以想象到是一件耗时耗力的事情。

梯度法来恰恰可以弥补上述的缺陷。

 

4.2.1 实现梯度的计算

梯度法优势在于可以一次计算出多个变量的偏导数，并汇总成向量，像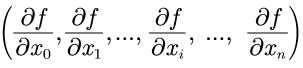这种汇总而成的向量，称为梯度（注： 来自 deep learning from scratch）。

接下来就是梯度的实现了，计算机是无法直接求出偏导数或者导数的，不过根据数学知识可以得到偏导数的近似值，因此可以：

对应的实现程序如下：

def numerical_gradient_1d(f, x):
    '''
数值微分，求f(x)的梯度
    :param f: 函数
    :param x: 梯度值
    :return: df在x处的导数
    '''
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx] # 缓存原来的值
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

        x[idx] = tmp_val # 原来的值

    return grad

以上是1D的梯度下降，我们可以扩展成2D的梯度下降函数numerical_gradient_2d：

def numerical_gradient_2d(f, X):
    if X.ndim == 1:
        return _numerical_gradient_1d(f, X)
    else:
        grad = np.zeros_like(X)

        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_1d(f, x)

        return grad

 

def numerical_gradient(f, x):
    '''
    数值微分，求f(x)的梯度
    :param f:
    :param x:
    :return:
    '''
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = tmp_val + h
        fxh1 = f(x) # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

        x[idx] = tmp_val # 恢复成原来的值
        it.iternext()

    return grad

 

4.2.2 验证梯度计算方法是否有用

作为一个严谨的程序员，自己 写的每一个模块至少需要做一次验证，以减少后期出现bug的调试；

 

在此，简单的验证 的在点上的梯度；

根据数学知识，可以知道梯度为：

那么

下面开始验证

片段1： function的实现：

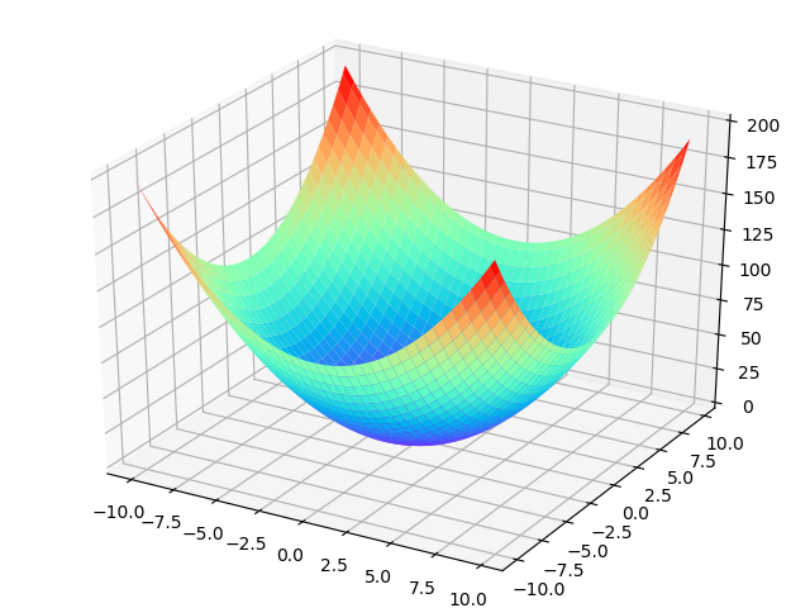
def function(x):
    return x[0]**2 + x[1]**2

function的坐标图如下, 可见整个函数的最小值在（0，0）处，因此点（3，4）的梯度方向应该指向（0，0），即：梯度值应该为正数。

from matplotlib import pyplot as plot  # 用来绘制图形
import numpy as np  # 用来处理数据
from mpl_toolkits.mplot3d import Axes3D  # 用来给出三维坐标系。
figure = plot.figure()

# 画出三维坐标系：
axes = Axes3D(figure)
X = np.arange(-10, 10, 0.25)
Y = np.arange(-10, 10, 0.25)
X, Y = np.meshgrid(X, Y) # 限定图形的样式是网格线的样式：
Z = function([X,Y])
axes.plot_surface(X, Y, Z, cmap='rainbow') # 绘制曲面，采用彩虹色着色：
# 图形可视化：
plot.show()

if __name__ == '__main__':
    # show()
    print(numerical_gradient(function, np.array([3.0,4.0])))

对应的输出：

[6. 8.]

验证正确, 说明grad的书写没有问题。

 

 

 

4.2.3梯度法的实现

神经网络学习的主要任务是在学习过程中寻找最优参数，这些参数使得loss function 取得最小值。这里的神经网络可以用g(x)表示。

一般来说，神经网络的参数空间较大，损失函数也较为复杂，往往会通过梯度来寻找g(x)的最小值。但需要注意：梯度表示的各个点处函数值减小最多的方向，无法保证是真正的应该进行梯度下降的方向。

尽管如此，沿着梯度的方向依旧是可以最大限度的找到减小损失函数的值。通过不断的向梯度的方向迈进，便会使得loss function逐渐减小(这个过程被称为 梯度法，gradient method)。

梯度法是解决机器学习中优化问题的常用方法，根据优化的目标可以分为： 梯度下降法和梯度上升法。

用数学表达为:

利用上面的公式和numerical_gradient，梯度法的实现如下：

def gradient_descent(f, init_x, learning_rate=0.01, step_num=200):
    '''
    通过一步一步的迭代，优化目标函数，找出使得目标函数最小的点
    :param f: 目标函数
    :param init_x: 初始位置
    :param learning_rate: 学习率
    :param step_num: 迭代次数
    :return:
    '''
    x = init_x
    for i in range(step_num):
        grad = numerical_gradient(f,x)
        x = x - learning_rate*grad # 公式的实现
    return x

if __name__ == '__main__':
    # show()
    #print(numerical_gradient(function, np.array([3.0,4.0])))
    min_value = gradient_descent(function, init_x=np.array([3.0,4.0]))
    print(min_value)

 

4.3 学习算法的实现

本节会阐述学习算法的伪代码，具体实现会在3.4给出。

神经网络的学习中使用到了梯度法（见3.2节），根据梯度法我们可以了解到神经网络学习的过程：可以按照以下4个步骤进行：

 

Step1：获取minibatch:

从数据集中选取一部分数据，这部分数据称为mini-batch，现在的目标就是减小minibatch 的loss fucntion value。

Step2：计算梯度值

为了减小loss function的值，求出各个权重参数的梯度。梯度是表示损失函数值减小最多的方向。

Step3：更新参数

梯度表示的是损失函数减小的方向；因此将权重参数沿着梯度所指的方向进行微小的更新。

Step4：迭代重复

重复Step1,2,3

 

以上使用的是梯度下降的方法，由于是随机选择的mini-batch数据（也就是说随机选择的初始点），所以称为 随机梯度下降（stochastic gradient descent）注：见Deep Learning from Scratch

 

4.4 基于mnist数据集的神经网络的训练

本节整合前面的代码，实现一个两层的神经网络。用mnist数据集训练，来了解整个学习的过程。整个过程会尽量简化.

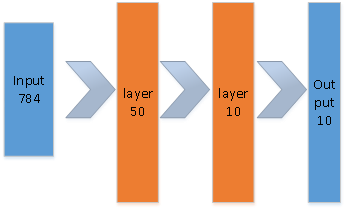
为了简化起见，网络输入层是784*1，有两个隐含层,神经元的数量分别是50和10; 由于输出层和上一层的输出数量一致,因此用恒等函数即可， 损失函数使用交叉熵。

网络结构如下：

网络结构的实现：

# -*- coding: utf-8 -*-
# @File  : two_layer_net.py
# @Author: lizhen
# @Date  : 2020/1/28
# @Desc  : 使用梯度的网络

from src.common.functions import *
from src.common.gradient import numerical_gradient
import numpy as np

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):

        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y

    # x:输入参数, t:label
    def loss(self, x, t):
        y = self.predict(x)

        return cross_entropy_error(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # x:输入参数, t:label
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}

        batch_num = x.shape[0]

        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)

        dz1 = np.dot(dy, W2.T)
        da1 = sigmoid_grad(a1) * dz1
        grads['W1'] = np.dot(x.T, da1)
        grads['b1'] = np.sum(da1, axis=0)

        return grads

 

训练代码：

# -*- coding: utf-8 -*-
# @File  : train_neuralnet.py
# @Author: lizhen
# @Date  : 2020/2/2
# @Desc  : 第三篇的实现： 利用梯度

import numpy as np
import matplotlib.pyplot as plt
from src.datasets.mnist import load_mnist
from src.test.two_layer_net import TwoLayerNet

# 获取训练数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000  # 迭代次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 计算梯度
    grad = network.numerical_gradient(x_batch, t_batch)
    # grad = network.gradient(x_batch, t_batch) # 较快

    # 更新权重
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc , loss | " + str(train_acc) + ", " + str(test_acc)+", "+str(loss))


# 绘制图
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')

plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

# plt.plot(train_loss_list,label='loss value')
# plt.show()

 

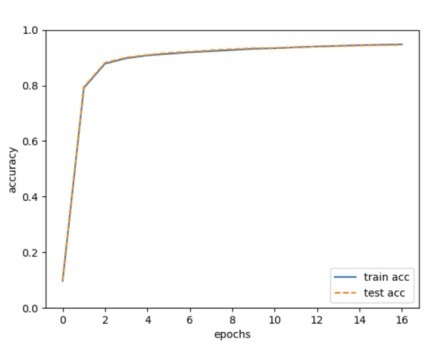
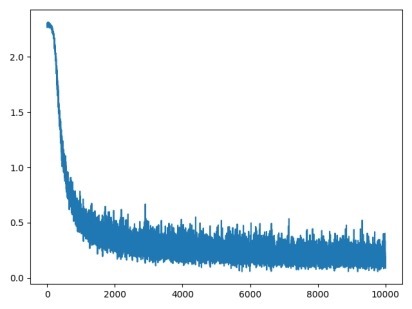
输出：

 

Loss 曲线图和acc变化曲线如下

2020年2月3日星期一