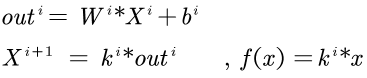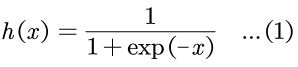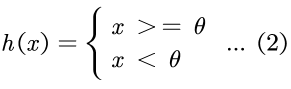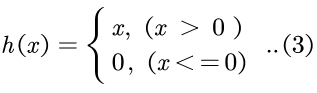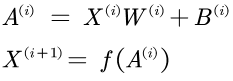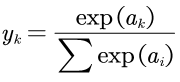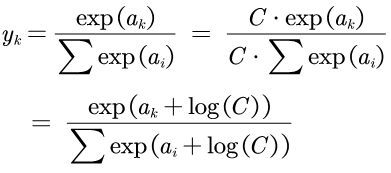Python 实现深度学习（3）: 神经网络的forward实现

 

写在最前：

写在最前, 我把代码和整理的文档放在github上了

https://github.com/Leezhen2014/python_deep_learning

 

 

Forward指的是神经网络推理，forward与感知机相比，多了一个激活函数的模块。因此本章需要实现激活函数，另外也需要重新实现y=w*x+b。本章的顺序如下：

 

3.1 激活函数的实现

在感知机中讲到用阈值来切换输出，这样的函数称为“阶跃函数”：一旦输入超出了阈值，就切换输出。阶跃函数也算是一种激励函数。

需要注意激励函数应该具有以下数学特性：

第一：由于后期训练过程中会对激励函数求导，因此这些函数必须符合数学上的可导。

第二：必须为非线性的函数。这可以用公式推一下：

若激励函数为线性函数

从本质上看，激活函数等同于原来的输入的:

 

即：

第i层的输入是第i+1层的k倍。

从表象上看，加深网络层次已经失去了意义；等效于无隐含层的网络。

 

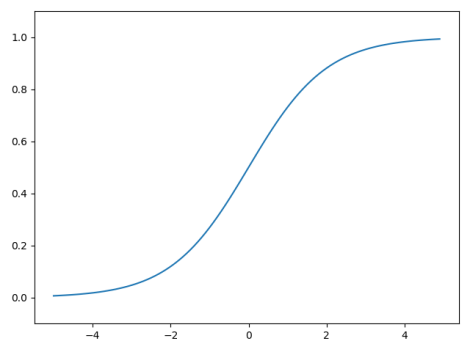
3.1.1 Sigmoid 函数的实现

Sigmoid函数在（-1,1）区间内变化较大，超出这个范围以后变化较小，可以很好的影响。

 

 

 

def Sigmoid(x):
    return 1/(np.exp(-x) +1)

if __name__ == '__main__':
    x = np.arange(-5.0, 5.0, 0.1)
    y = Sigmoid(x)

    plt.plot(x,y)
    plt.ylim(-0.1,1.1)
    plt.show()

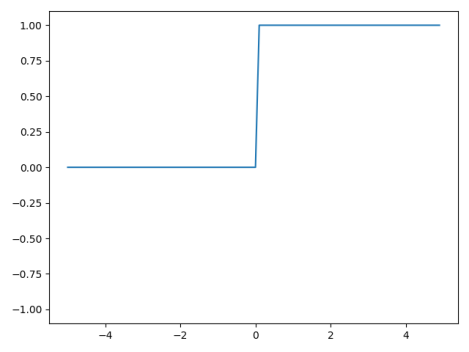
3.1.2 阶跃函数

def step_func(x):
    temp = x.copy()
    temp = np.where(x > 0, temp, 0)
    temp = np.where(x <= 0, temp, 1)
    return temp


if __name__ == '__main__':
    x = np.arange(-5.0, 5.0, 0.1)

    y = step_func(x)

    plt.plot(x,y)
    plt.ylim(-1.1,1.1)
    plt.show()

 

 

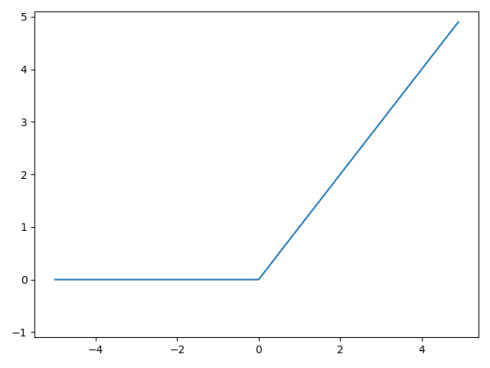
3.1.3 Relu 系列

 

 

Relu(Rectified Linear Unit) 函数在输入值大于0的情况下保持不变，在输入值小于0的情况下，输出等于0。

阶跃函数和sigmoid函数都属于非线性的函数，

def Relu(x):
    return np.maximum(0,x)

if __name__ == '__main__':
    x = np.arange(-5.0, 5.0, 0.1)

    y = Relu(x)

    plt.plot(x,y)
    plt.ylim(-1.1,5.1)
    plt.show()

 

 

3.2 forward的流程

主要是介绍y=WX+b的实现。神经网络的forward本质是多维数组的运算+激励函数。激活函数已经实现了，因此只要将多维数组的运算了解清楚，便可以实现forward。forward的流程如下：

p.s.: f即为激活函数

本质上是矩阵的乘法，借助np.dot可以实现；在此不赘述。

 

3.3 输出层的设计与实现

目前来看，神经网络在分类的问题上可以大致分为两类：

1. 分类问题：数据属于哪个类别，可以使用恒等函数，直接获取预测结果。

2. 回归问题：根据输入，预测一个连续的数值问题。可以使用softmax。

Ps:  分类问题的输出层也是可以使用softmax的，只不过用softmax以后得到的数值是一个线性的数值，还需要选取阈值才能划分为类别。

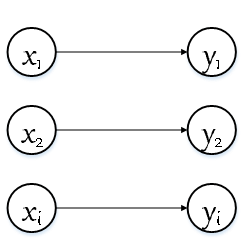
恒等函数是不需要实现了，神经网络的输出节点就是label的输出，如下图所示：

Softmax函数的数学公式如下：

Equation 3 softmax函数

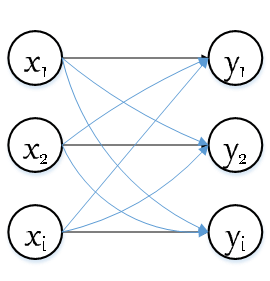
从公式中可以看出，输出层的各个神经元的输出都会受到输入信号的影响，如下图所示。

Figure 3 softmax 的表达图

def softmax(x):
    '''
    softmax 实现，没有考虑数值溢出
    :param x: ndarray
    :return: y, ndarray
    '''
    a = np.exp(x)
    sum_exp = np.sum(a)
    y= a/sum_exp
    return y

 

上图的代码是按照公式实现的，但是没有考虑数值溢出的情况；由于是exp是指数函数，当指数特别大的时候，进行除法的时候会的时候会出现数值溢出。为了避免以上情况，将分子和分母同时乘上常量C（必须足够大）

 

def softmax(x):
    '''
    softmax 实现
    :param x: ndarray
    :return: y, ndarray
    '''
    C = np.max(x)
    exp_a = np.exp(x - C)
    sum_exp = np.sum(exp_a)
    y= exp_a / sum_exp
    return y

 

3.4测试神经网络的推理

在经过上述的准备工作后， 我们就可以组装成一个简单的推理网络；

假设， 我们的神经网络是简单的全连接层， 且手里已经有了网络的权重（sample_weight.pkl）。

我们要做的是对minst手写体识别，数据集用load_mnist（）方法获取。

具体代码可以看github: https://github.com/Leezhen2014/python_deep_learning

# -*- coding: utf-8 -*-
# @File  : day7.py
# @Author: lizhen
# @Date  : 2020/2/4
# @Desc  : 第二篇的实现: 对文件的实现

import sys, os
import numpy as np
import pickle
from src.datasets.mnist import load_mnist
from src.common.functions import sigmoid, softmax


def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("../datasets/sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p= np.argmax(y)
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

 

打印输出正确率：

输出：

Accuracy: 0.9352

 

 

------------------------

好了，今天到此为止。