第十二届蓝桥杯C++ B组

A：计算256MB能够存放多少个int

int main()
{
    cout<<256*1024*1024/4;
    return 0;
}

ans=67108864

 

B：计算2021张1到10的卡片能够拼出1~n的最大的n

int cnt[10];
int main()
{
    for(int i=0;i<10;i++) cnt[i]=2021;
    int k=1;
    while(1){
        int t=k;
        while(t) cnt[t%10]--,t/=10;
        for(int i=0;i<10;i++)
            if(cnt[i]<0){
                cout<<k-1;
                return 0;
            }
        k++;
    }
    return 0;
}

ans=3181

 

C：给定一个20*21的棋盘，任选两点，问有多少条直线。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double,double> PII;
const double eps=1e-6;
struct node{
    double k,b;
    bool operator<(const node& t)const{
        if(fabs(k-t.k)<eps) return b<t.b;
        return k<t.k;
    }
};
vector<node> v;
int main()
{
    for(int x1=0;x1<20;x1++){
        for(int y1=0;y1<21;y1++){
            for(int x2=0;x2<20;x2++){
                for(int y2=0;y2<21;y2++){
                    if(x1!=x2){
                        double k=double(y2-y1) / (x2-x1);
                        double b=y1-k*x1;
                        v.push_back({k,b});
                    }
                }
            }
        }
    }
    sort(v.begin(),v.end());
    int res=1;
    for(int i=1;i<v.size();i++){
        if(fabs(v[i].k-v[i-1].k)>eps||fabs(v[i].b-v[i-1].b)>eps)
            res++;
    }
    cout<<res+20;
    return 0;
}

ans=40257

 

D：给定一个很大的数，问差分成3个数相乘有多少种方案，1*2*2和2*2*1是不同的方案。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n=2021041820210418;
vector<LL> p;
int main()
{
    LL t=n;
    for(LL i=1;i<=n/i;i++){
        if(t%i==0){
            p.push_back(i);
            if(t/i!=i)
                p.push_back(t/i);
        }
    }
    LL res=0;
    for(int i=0;i<p.size();i++){
        for(int j=0;j<p.size();j++){
            for(int k=0;k<p.size();k++){
                if(p[i]*p[j]*p[k]==n){
                    res++;
                }
            }
        }
    }
    cout<<res;
    return 0;
}

ans=2430

 

E：裸的最短路问题。(当时用的floyd，因为好写)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=2050;
const int INF=0x3f3f3f3f;
int f[N][N];
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}
int main()
{
    memset(f,0x3f,sizeof f);
    for(int i=1;i<=2021;i++){
        for(int j=1;j<=2021;j++){
            if(abs(i-j)<=21){
                int tmp=i*j/gcd(i,j);
                f[i][j]=tmp;
                f[j][i]=tmp;
            }
        }
    }
    for(int k=1;k<=2021;k++){
        for(int i=1;i<=2021;i++){
            for(int j=1;j<=2021;j++){
                if(f[i][k]!=INF&&f[k][j]!=INF){
                    f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
                }
            }
        }
    }
    cout<<f[1][2021];
    return 0;
}

ans=10266837

 

F：时间显示

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
    long long n;
    cin>>n;
    n/=1000;
    n%=24*60*60;
    int h=n/(60*60);
    n%=60*60;
    int m=n/60;
    n%=60;
    int s=n;
    printf("%02d:%02d:%02d",h,m,s);
    return 0;
}

 

G：背包问题，但是需要加上一个偏移量

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=110;
const int M=2e5+10,B=M/2;
int w[N];
bool f[N][M];
int main()
{
    int n,m=0;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>w[i],m+=w[i];
    f[0][0+B]=1;
    for(int i=1;i<=n;i++){
        for(int j=-m;j<=m;j++){
            f[i][j+B]=f[i-1][j+B];
            if(j-w[i]>=-m) f[i][j+B]|=f[i-1][j-w[i]+B];
            if(j+w[i]<=m) f[i][j+B]|=f[i-1][j+w[i]+B];
        }
    }
    int res=0;
    for(int i=1;i<=m;i++)
        if(f[n][i+B])
            res++;
    cout<<res;
    return 0;
}

 

H：杨辉三角形。

说实话挺复杂的，将杨辉三角形斜着看。

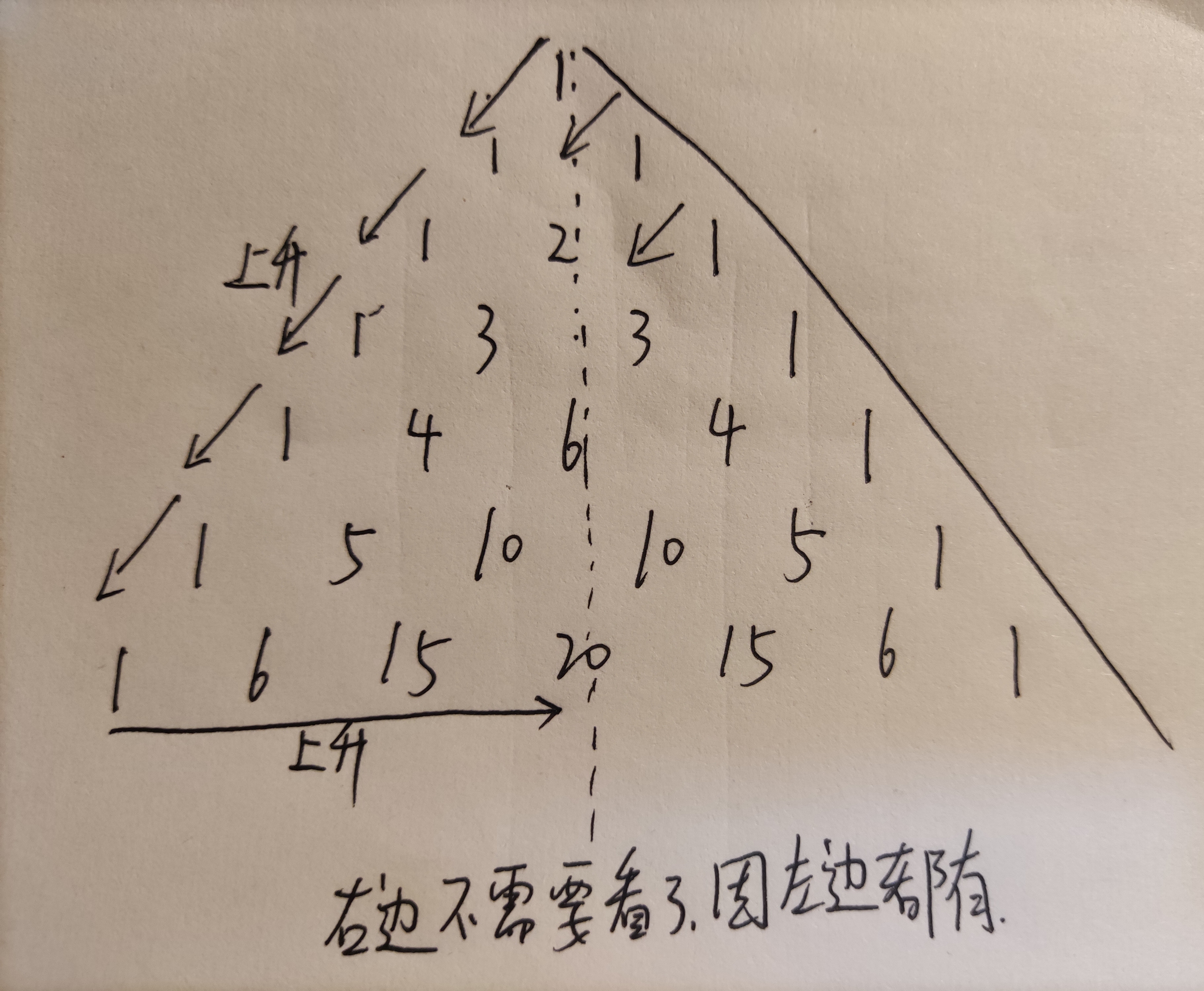
右半边可以直接不看了，因为右边的左边都有，所以一定更先出现。

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

越靠近中间列的增加的越快。

我们得先从中间开始找n，对于每一列找到大于等于n的最小的数，若他是n的话则他就是答案了。

否则找前面一列的，可以发现答案是必然存在的（看第二列）。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n;
LL C(LL a,LL b){
    LL res=1;
    for(int i=a,j=1;j<=b;i--,j++){
        res=res*i/j;
        if(res>n) return res;
    }
    return res;
}
bool check(LL k){
    LL l=2*k,r=n;//左端点为第2*k行，右端点为第n行
    while(l<r){
        LL mid=l+r>>1;
        if(C(mid,k)>=n) r=mid;
        else l=mid+1;
    }
    if(C(r,k)!=n) return false;
    cout<<r*(r+1)/2 + k+1;
    return true;
}
int main()
{
    cin>>n;
    if(n==1){
        cout<<1<<endl;
        return 0;
    }
    for(int i=16;;i--){
        if(check(i)){
            break;
        }
    }
    return 0;
}

 

I：非常复杂的一道题。

因为n，m<=1e5，若是直接排序n*m*logn，肯定会超时的。

可以通过栈来解这道题。

在翻转的过程中虚线部份就已经确定了。

#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N=1e5+10;
PII stk[N];
int top=0;
int ans[N];
int main()
{
    int n,m;
    cin>>n>>m;
    while(m--){
        int p,q;
        cin>>p>>q;
        if(p==0){
            while(top&&stk[top].x==0) q=max(q,stk[top--].y);
            while(top>=2&&q>=stk[top-1].y) top-=2;
            stk[++top]={0,q};
        }else if(top){
            while(top&&stk[top].x==1) q=min(q,stk[top--].y);
            while(top>=2&&q<=stk[top-1].y) top-=2;
            stk[++top]={1,q};
        }
    }
    //以上是找出正确的操作。
    int k=n,l=1,r=n;
    for(int i=1;i<=top;i++){
        if(stk[i].x==0){
            while(r>stk[i].y&&l<=r) ans[r--]=k--;
        }else if(stk[i].x==1){
            while(l<stk[i].y&&l<=r) ans[l++]=k--;
        }
        if(l>r) break;
    }
    if(top%2)//若是没放完的话
        while(l<=r) ans[l++]=k--;
    else 
        while(l<=r) ans[r--]=k--;
    for(int i=1;i<=n;i++)
        cout<<ans[i]<<" ";
    return 0;
}

 

J：巨难的一道题。

1、括号序列合法的充要条件：左括号和右括号数目相等，且任意前缀左括号数目>=右括号数目
2、向不合法的括号序列中添加括号能否单独考虑左右括号？
　　可以，因为若是不存在左括号和右括号放在同一个空隙里的话，必然是可以的。
　　　　　　　若是存在左括号与右括号放到同一个空隙里的话只有可能是" ))))((( "这种情况。
3、此时可以单独考虑左括号，那么如何保证考虑左括号的时候不会有重复的情况？
　　比如 ) ) 能够添加成 ( ( ) ) ，但是这会有两种解释一是在0前面添加两个左括号，或者在0前面以及1前面各添加一个左括号。
　　可以发现右括号将整个序列分成了3个左括号段，一个括号序列被每一段左括号的数目唯一确定。我们固定只能在) 前面添加(。
4、计算向序列中添加左括号的方案数。
　　DP。

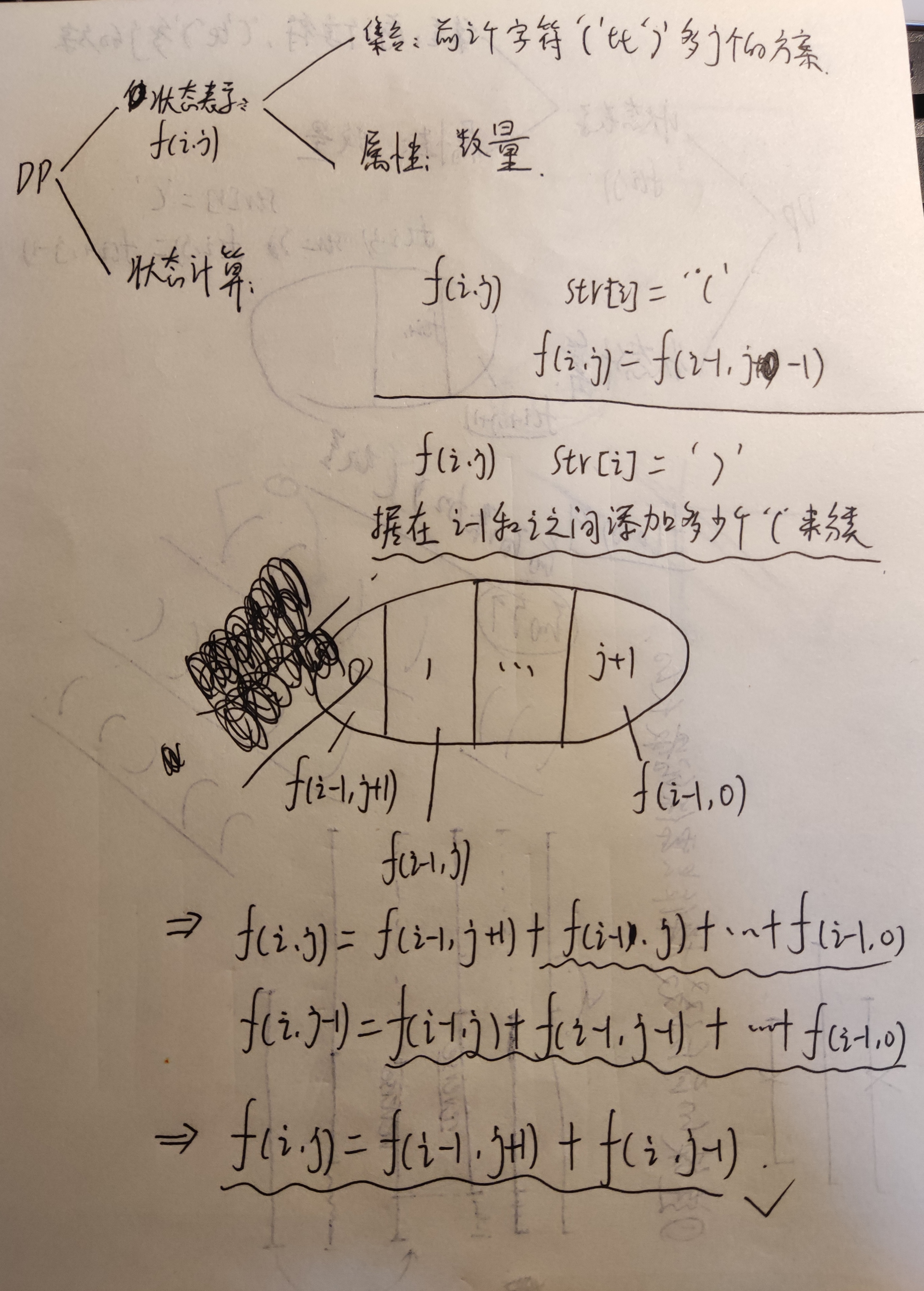
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=5010,mod=1e9+7;
char str[N];
LL f[N][N];
LL n;
LL calc(){
    memset(f,0,sizeof f);
    f[0][0]=1;
    for(int i=1;i<=n;i++){
        if(str[i]=='('){
            for(int j=1;j<=n;j++)
                f[i][j]=f[i-1][j-1];
        }else if(str[i]=')'){
            f[i][0]=(f[i-1][0]+f[i-1][1])%mod;
            for(int j=1;j<=n;j++)
                f[i][j]=(f[i-1][j+1]+f[i][j-1])%mod;
        }
    }
    for(int i=0;i<=n;i++){
        if(f[n][i])
            return f[n][i];
    }
    return -1;
}
int main()
{
    cin>>str+1;
    n=strlen(str+1);
    LL l=calc();
    reverse(str+1,str+1+n);
    for(int i=1;i<=n;i++)
        if(str[i]=='(') str[i]=')';
        else str[i]='(';
    LL r=calc();
    cout<<l*r%mod;
    return 0;
}