leetcode周赛 239

A:水题，直接枚举即可。

class Solution {
public:
    int getMinDistance(vector<int>& nums, int target, int start) {
        int res=0,seq=INT_MAX;
        for(int i=0;i<nums.size();i++){
            if(nums[i]==target&&abs(i-start)<seq){
                seq=abs(i-start);
                res=i;
            }
        }
        return abs(start-res);
    } 
};

 

B:直接枚举每一段有多少个字母就好了时间（2e19），不过得注意有19位，所以得用ULL来存。

考试写的dfs版本：

typedef unsigned long long LL;
class Solution {
public:
    bool res=false;
    LL get(LL l,LL r,string s){
        LL res=0;
        for(LL i=l;i<=r;i++){
            res=res*10+s[i]-'0';
        }
        return res;
    }
    void dfs(LL now,LL pre,string& s,LL cnt){
        if(now>=s.size()&&cnt>=2){
            res=true;
            return ;
        }
        for(LL i=now;i<s.size();i++){
            LL num=get(now,i,s);
            if((now==0&&num<pre)||num==pre-1){
                dfs(i+1,num,s,cnt+1);
            }
        }

    }
    bool splitString(string s) {
        dfs(0,0x3f3f3f3f3f3f3f3f,s,0);
        return res;
    }
};

 

二进制枚举版本：

typedef unsigned long long LL;
class Solution {
public:
    bool splitString(string s) {
        int n=s.size();
        for(int i=1;i < 1<<(n-1);i++){//i是四位，从1开始是至少有一个分割线
            unsigned long long x=s[0]-'0';
            unsigned long long pre=-1;//补码，全一
            bool flag=true;
            for(int j=0;j<n-1;j++){
                if(i>>j&1){
                    if(pre!=-1&&x!=pre-1){
                        flag=false;
                        break;
                    }
                    pre=x;
                    x=s[j+1]-'0';
                }else{
                    x=x*10+s[j+1]-'0';
                }
            }
            if(x!=pre-1) flag=false;
            if(flag) return true;
        }
        return false;
    }
};

 

C:考试的时候想的并不是很明白，复习的时候发现考察逆序对的问题，考试的时候阴差阳错的用冒泡的思想解决了。

考试的时候的代码：

class Solution {
public:
    int getMinSwaps(string num, int k) {
        string tnum=num;
        for(int i=0;i<k;i++)
            next_permutation(tnum.begin(),tnum.end());
        int res=0;
        for(int i=0;i<num.size();i++){
            if(num[i]!=tnum[i]){
                int tar=i+1;
                while(num[i]!=tnum[tar]) tar++;
                for(int j=tar;j>i;j--){
                    swap(tnum[tar],tnum[tar-1]);
                    tar--;
                    res++;
                }
            }
        }
        return res;
    }
};

补题时候的代码：

还存在一个问题就是如果存在两个相同的元素的话如何对应。

 

 

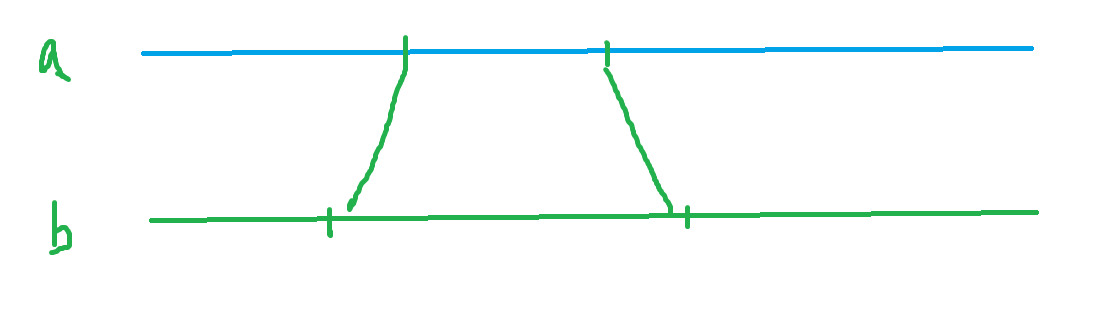
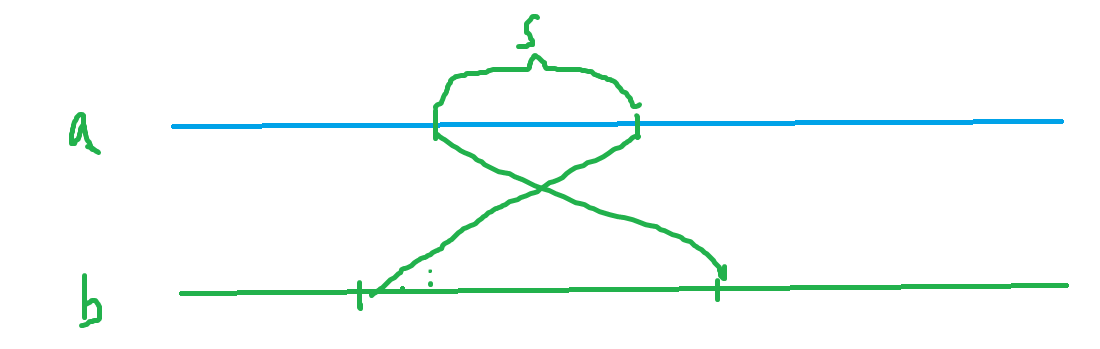
因为只能交换相邻元素，显而易见是第一种，第二种会多出2*s的交换次数。

class Solution {
public:
    int getMinSwaps(string a, int k) {
        string b=a;
        for(int i=0;i<k;i++)
            next_permutation(b.begin(),b.end());
        int n=b.size();
        vector<int> c(n);//存储a中的元素在b中的位置
        vector<bool> vis(n);
        for(int i=0;i<n;i++){
            char ca=a[i];
            for(int j=0;j<n;j++){
                if(!vis[j]&&ca==b[j]){
                    c[i]=j;
                    vis[j]=true;
                    break;
                }
            }
        }
        //目的：把c变成正序
        //因为n=1e3,冒泡排序即可，若n过大的话，得用归并
        int res=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<n-i-1;j++){
                if(c[j]>c[j+1]){
                    swap(c[j],c[j+1]);
                    res++;
                }
            }
        }
        return res;
    }
};

 

 

D：可以用并查集做，这是个经典模型（参考AcWing疯狂的馒头）

并查集初始化之后，我们将优先级高的先操作，本题优先级高的就是区间长度短的。

每次区间操作之后将一个区间删除（方法是让每一个都指向他的后一个元素），同时记录每一个元素对应的答案。

class Solution {
public:
    vector<int> p,w;
    vector<int> minInterval(vector<vector<int>>& segs, vector<int>& queries) {
        sort(segs.begin(),segs.end(),[](vector<int>&a,vector<int>&b){
            return a[1]-a[0]+1 < b[1]-b[0]+1;
        });
        const int n=1e7+10;
        p.resize(n+1);
        w.resize(n+1,-1);
        for(int i=0;i<=n;i++) p[i]=i;
        for(auto& s:segs){
            int l=s[0],r=s[1];
            int len=s[1]-s[0]+1;
            while(find(l)<=r){
                l=find(l);
                w[l]=len;
                p[l]=l+1;
            }
        }
        vector<int> res;
        for(auto& q:queries){
            res.push_back(w[q]);
        }
        return res;
    }
    int find(int x){
        if(p[x]!=x)
            p[x]=find(p[x]);
        return p[x];
    }
};

但是因为本题n为1e7，时间复杂度为nlogn，会超时

观察到区间数目和查询数目只有1e5，可以用离散化优化

class Solution {
public:
    vector<int> xs;
    vector<int> p,w;
    vector<int> minInterval(vector<vector<int>>& segs, vector<int>& queries) {
        for(auto& s:segs) xs.push_back(s[0]),xs.push_back(s[1]);
        for(auto& q:queries) xs.push_back(q);
        sort(xs.begin(),xs.end());
        xs.erase(unique(xs.begin(),xs.end()),xs.end());
        //以上为离散化
        sort(segs.begin(),segs.end(),[](vector<int>&a,vector<int>&b){
            return a[1]-a[0]+1 < b[1]-b[0]+1;
        });
        int n=xs.size();
        p.resize(n+1);
        w.resize(n+1,-1);
        for(int i=0;i<=n;i++) p[i]=i;
        for(auto& s:segs){
            int l=get(s[0]),r=get(s[1]);
            int len=s[1]-s[0]+1;
            while(find(l)<=r){
                l=find(l);
                w[l]=len;
                p[l]=l+1;
            }
        }
        vector<int> res;
        for(auto& q:queries){
            res.push_back(w[get(q)]);
        }
        return res;
    }
    int find(int x){
        if(p[x]!=x)
            p[x]=find(p[x]);
        return p[x];
    }
    int get(int x){
        return lower_bound(xs.begin(),xs.end(),x)-xs.begin();
    }
};