https://www.acwing.com/problem/content/293/
给定一个空矩阵,问用1*2的矩形将其填满存在多少种方案。
可以只考虑一种,如果横的都已经确定了,那么竖的只有0或者1种放法,所以只考虑横的就好了(只考虑竖的也行)
暴搜复杂度为O(N! * M!),所以只能考虑动态规划,用一个整数表示一列的状态。
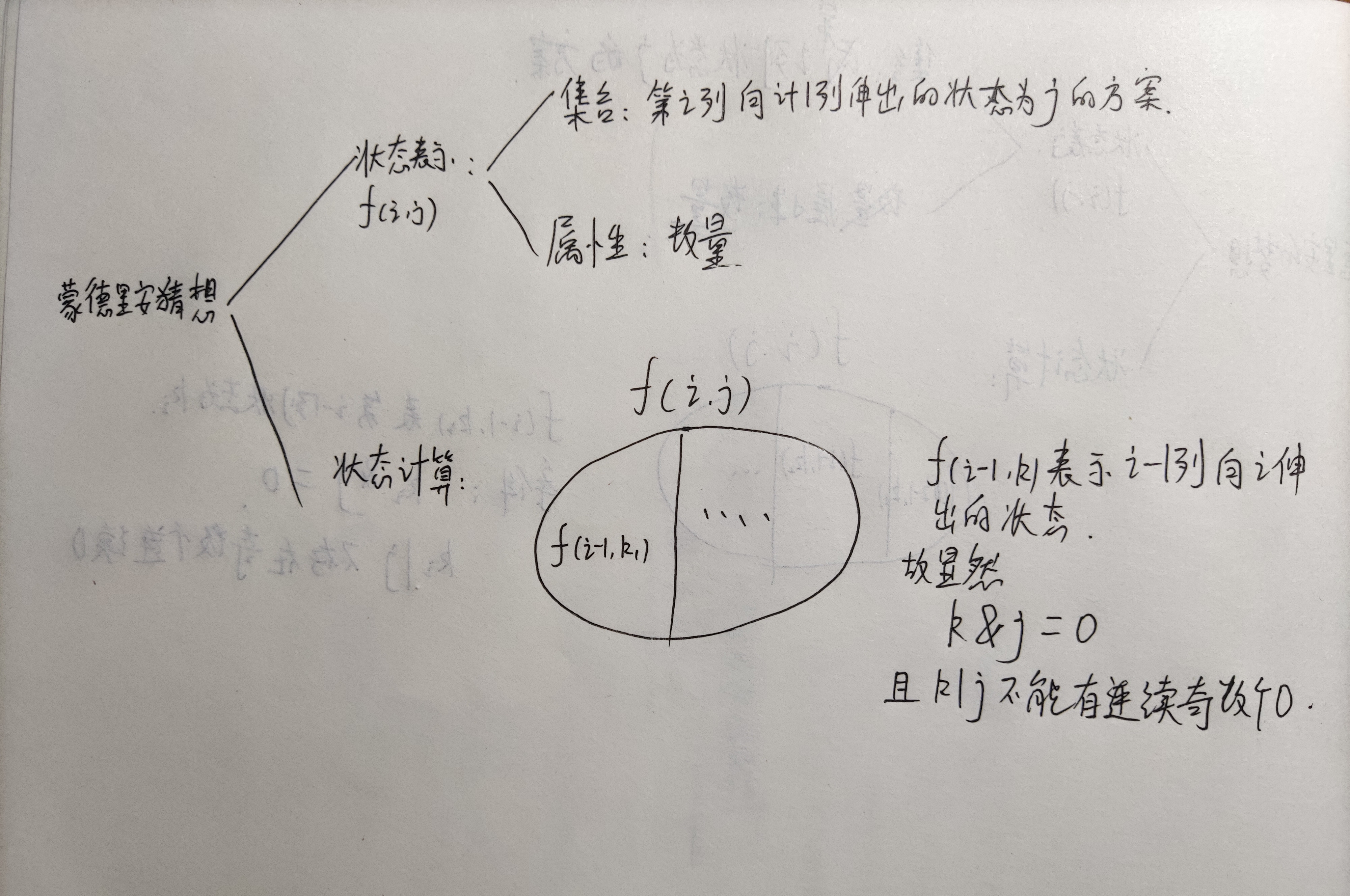
朴素写法:
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 const int N=12,M=1<<12; 5 long long f[N][M]; 6 bool st[M]; 7 int main(void){ 8 int n,m; 9 while(cin>>n>>m,n||m){ 10 for(int i=0;i< 1<<n;i++){ 11 int cnt=0; 12 st[i]=true; 13 for(int j=0;j<n;j++){ 14 if(i>>j&1){ 15 if(cnt&1){ 16 st[i]=false; 17 cnt=0; 18 } 19 }else{ 20 cnt++; 21 } 22 } 23 if(cnt&1){ 24 st[i]=false; 25 } 26 }//预处理全部的状态。 27 memset(f,0,sizeof f); 28 f[0][0]=1; 29 for(int i=1;i<=m;i++){ 30 for(int j=0;j<1<<n;j++){ 31 for(int k=0;k<1<<n;k++){ 32 if((j&k)==0&&st[j|k]){ 33 f[i][j]+=f[i-1][k]; 34 } 35 } 36 } 37 } 38 cout<<f[m][0]<<endl; 39 40 } 41 return 0; 42 }
预处理好j对应的状态
1 #include<iostream> 2 #include<cstring> 3 #include<vector> 4 using namespace std; 5 const int N=12,M=1<<12; 6 long long f[N][M]; 7 bool st[M]; 8 vector<int> state[M]; 9 int main(void){ 10 int n,m; 11 while(cin>>n>>m,n||m){ 12 for(int i=0;i< 1<<n;i++){ 13 int cnt=0; 14 st[i]=true; 15 for(int j=0;j<n;j++){ 16 if(i>>j&1){ 17 if(cnt&1){ 18 st[i]=false; 19 cnt=0; 20 } 21 }else{ 22 cnt++; 23 } 24 } 25 if(cnt&1){ 26 st[i]=false; 27 } 28 }//预处理全部的状态。 29 for(int j=0;j < 1<<n;j++){ 30 state[j].clear(); 31 for(int k=0;k< 1<<n;k++){ 32 if((j&k)==0&&st[j|k]){ 33 state[j].push_back(k); 34 } 35 } 36 } 37 memset(f,0,sizeof f); 38 f[0][0]=1; 39 for(int i=1;i<=m;i++){ 40 for(int j=0;j<1<<n;j++){ 41 for(auto k:state[j]){ 42 f[i][j]+=f[i-1][k]; 43 } 44 } 45 } 46 cout<<f[m][0]<<endl; 47 48 } 49 return 0; 50 }
https://www.acwing.com/problem/content/93/
最短Hamilton路径,dfs写不了,因为复杂度为O(n!)。
只能用dp。
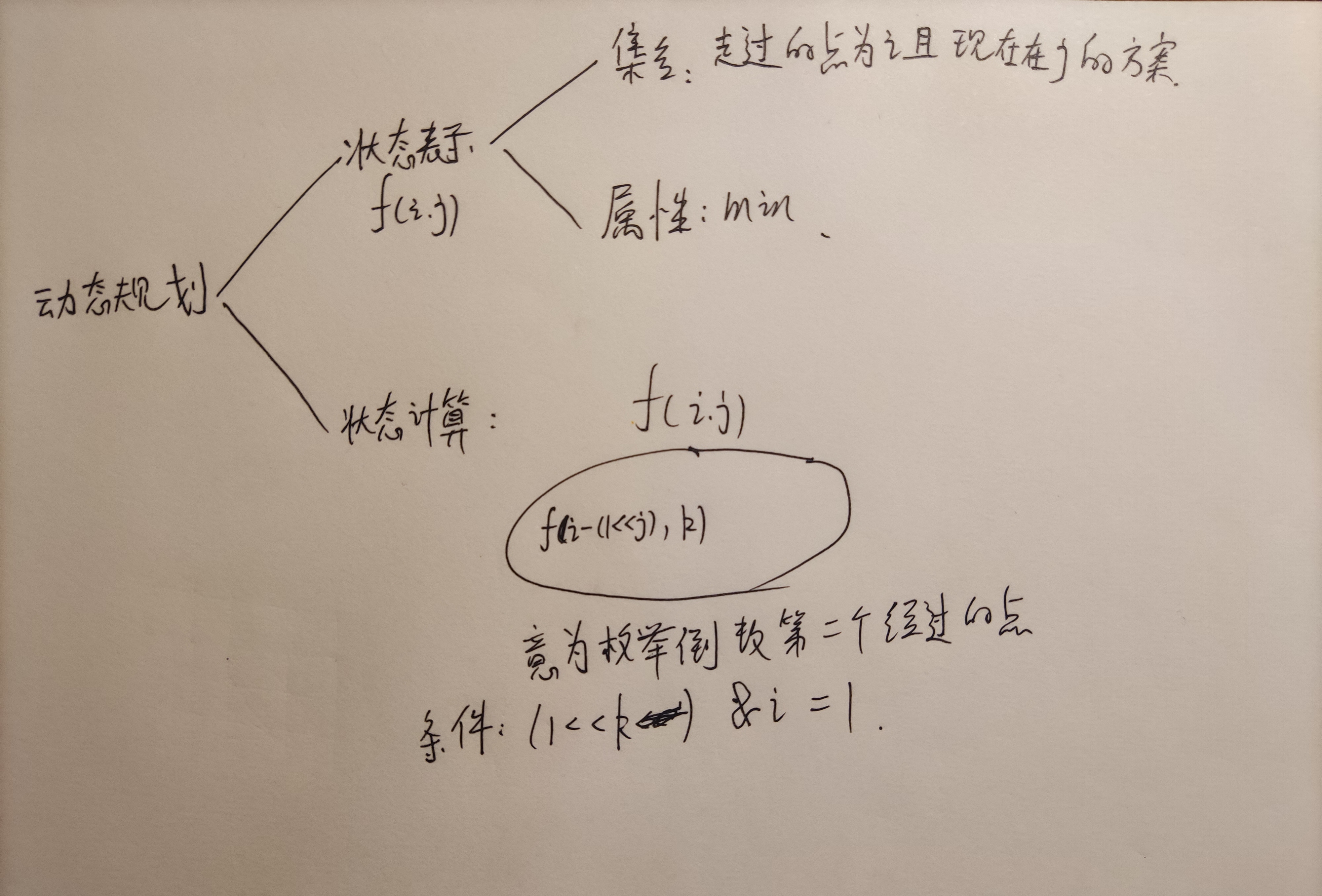
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 const int N=20; 5 int w[N][N]; 6 int f[1<<N][N]; 7 int main(void){ 8 int n; 9 cin>>n; 10 for(int i=0;i<n;i++){ 11 for(int j=0;j<n;j++){ 12 cin>>w[i][j]; 13 } 14 } 15 memset(f,0x3f,sizeof f); 16 f[1][0]=0; 17 //先枚举状态是因为后面需要用到前面的状态 18 for(int i=0;i<1<<n;i++){//枚举状态 19 for(int j=0;j<n;j++){//枚举每一个点,如果i中有这个点,就枚举倒数第二个点 20 if((1<<j)&i){ 21 for(int k=0;k<n;k++){ 22 if((1<<k)&i){ 23 f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]); 24 } 25 } 26 } 27 } 28 } 29 cout<<f[(1<<n)-1][n-1]; 30 return 0; 31 }




