动态规划--计数类DP

https://www.acwing.com/problem/content/902/

整数划分问题，给定一个正整数n，问有多少种方案使得n=x1+x2+...+xn，不考虑顺序。

解法1：利用完全背包的模型，将1~n每一个数字看成一个物品。

 

 

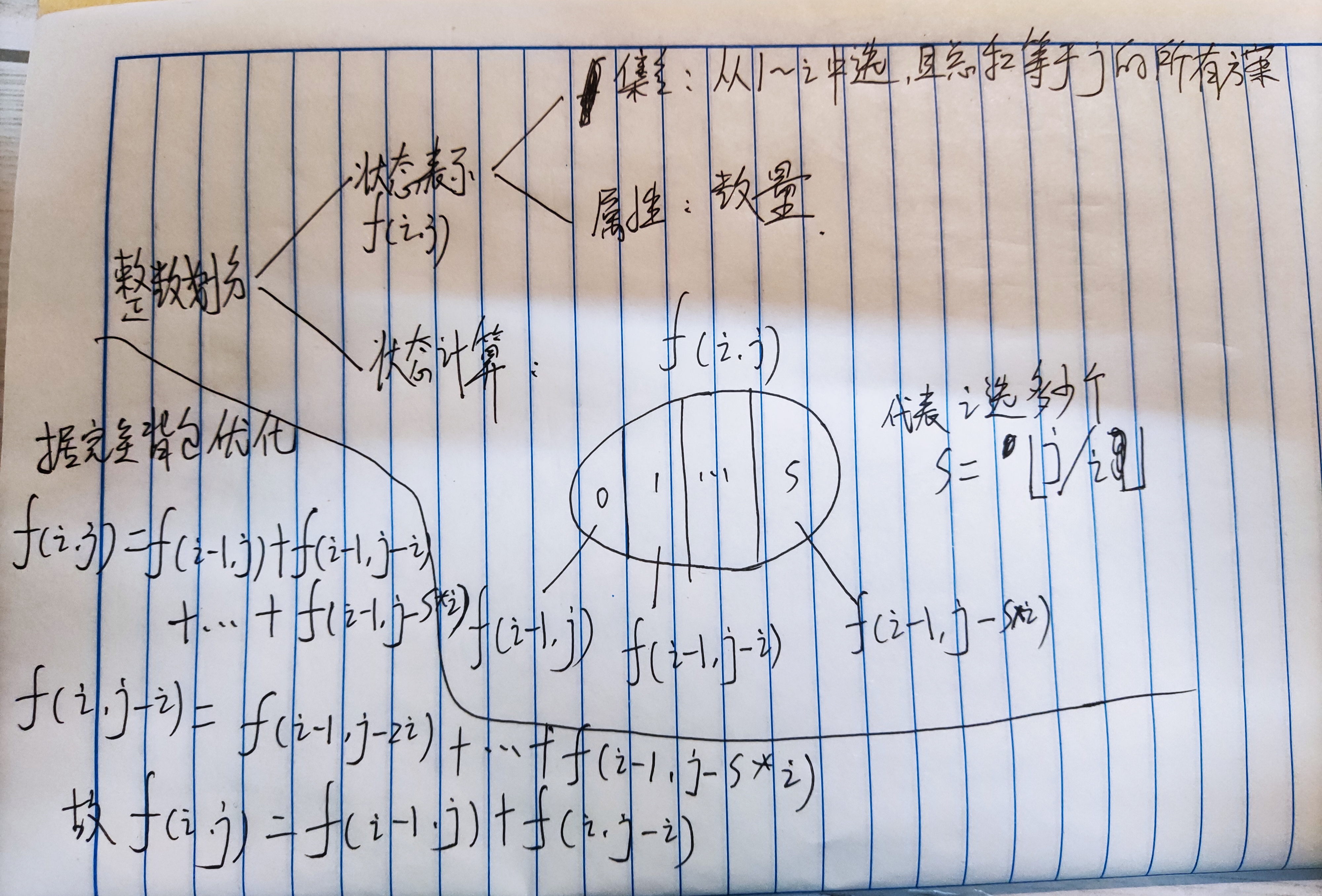
#include<iostream>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N][N];
int main(void){
    int n;
    cin>>n;
    for(int i=0;i<=n;i++) f[i][0]=1;//初始化，表示在前i个中选，和为0的方案数都为1
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            f[i][j]=f[i-1][j];
            if(j>=i) f[i][j]+=f[i][j-i];
            f[i][j]%=mod;
        }
    }
    cout<<f[n][n];
    return 0;
}

 

空间优化

#include<iostream>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N];
int main(void){
    int n;
    cin>>n;
    f[0]=1;
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j++){
            f[j]=(f[j]+f[j-i])%mod;
        }
    }
    cout<<f[n];
    return 0;
}

 

解法2:

 

 

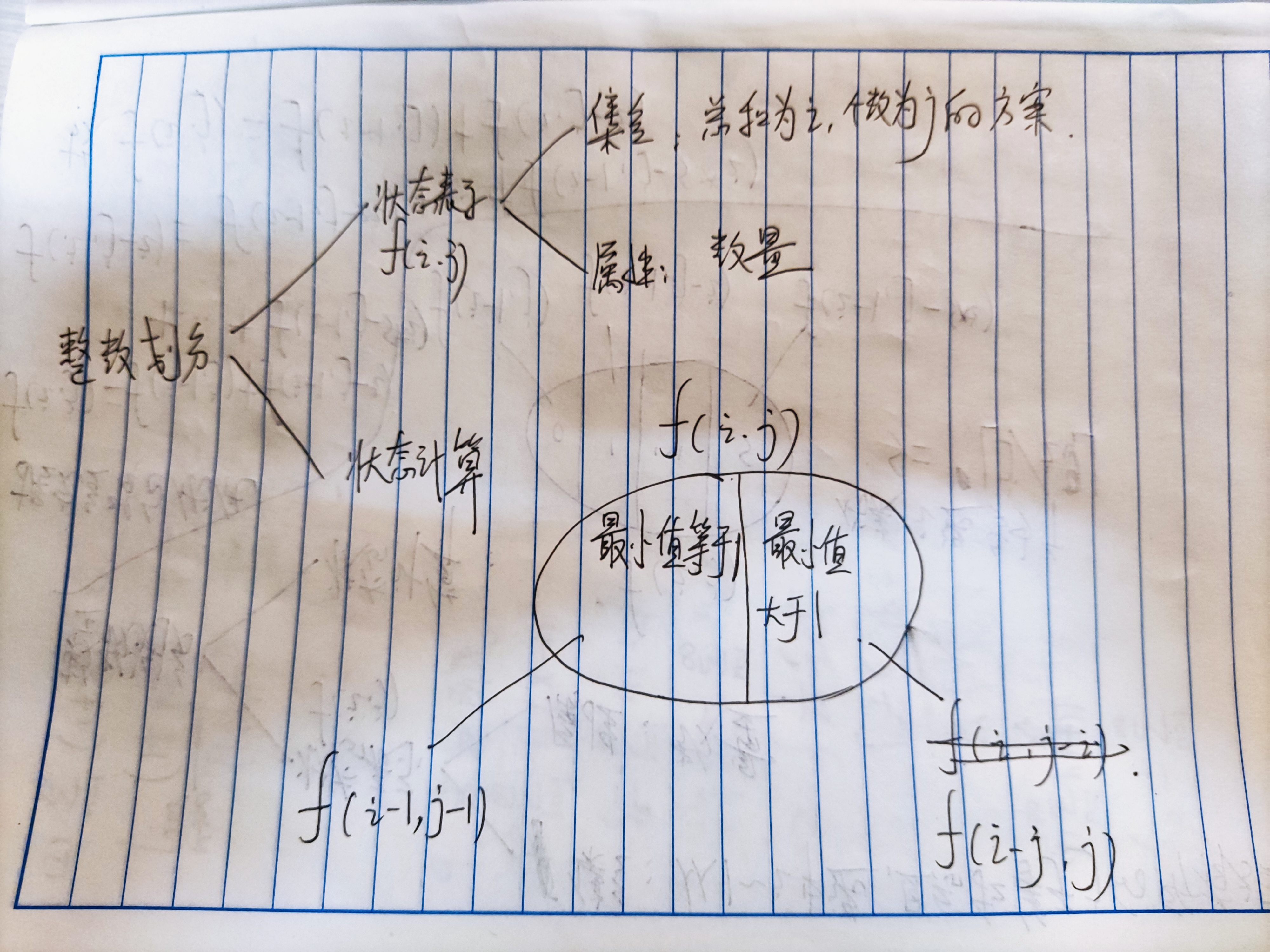
#include<iostream>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N][N];
int main(void){
    int n;
    cin>>n;
    f[1][1]=1;//表示总和为1，个数为1的方案数为1.
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            f[i][j]=(f[i-1][j-1]+f[i-j][j])%mod;
        }
    }
    int res=0;
    for(int i=1;i<=n;i++) res=(res+f[n][i])%mod;
    cout<<res;
    return 0;
}