临时算法
算法题
一、链表
1. 反转链表
如当输入链表{1,2,3}时,经反转后,原链表变为{3,2,1},所以对应的输出为{3,2,1}。以上转换过程如下图所示:

示例:
输入:{1,2,3}
返回值:{3,2,1}
代码:
public class Solution {
public ListNode ReverseList(ListNode head) {
if(head==null || head.next==null) return head;
ListNode newHead = ReverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
2. 链表内指定区间反转
将链表 m 位置到 n 位置之间的区间反转,要求时间复杂度 O(n),空间复杂度 O(1)。
示例:
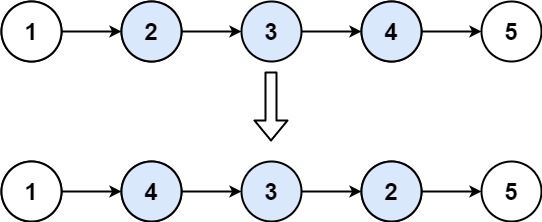
输入:head = [1,2,3,4,5], m = 2, n = 4
输出:[1,4,3,2,5]
代码:
public class Solution {
public ListNode reverseBetween (ListNode head, int m, int n) {
ListNode temp = new ListNode(-1);
temp.next = head;
ListNode pre = temp;
for(int i=1; i<m; i++) {
pre = pre.next;
}
ListNode tail = pre;
for(int i=m; i<=n; i++) {
tail = tail.next;
}
ListNode leftNode =pre.next;
ListNode nextNode = tail.next;
pre.next = null;
tail.next = null;
pre.next = reverseList(leftNode);
leftNode.next = nextNode;
return temp.next;
}
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) return head;
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
3. 链表中的节点每k个一组反转
将给出的链表中的节点每 k 个一组翻转,如果链表中的节点数不是 k 的倍数,将最后剩下的节点保持原样
示例:
输入:{1,2},3
输出:{1,2}
示例:
输入:{1,2,3,4,5},2
返回值:{2,1,4,3,5}
代码:
每k个递归 + reverseList方法
public class Solution {
public ListNode reverseKGroup (ListNode head, int k) {
if(head == null || k==1) return head;
ListNode pre = head;
for(int i=0; i<k-1; i++) {
pre=pre.next;
if(pre == null){
return head;
}
}
ListNode nextNode = pre.next;
pre.next = null;
ListNode newHead = reverseList(head);
head.next = reverseKGroup(nextNode, k);
return newHead;
}
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) return head;
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
4. 合并两个排序的链表
输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围: 0≤n≤1000,−1000≤节点值≤1000
要求:空间复杂度 O(1),时间复杂度O(n)

示例:
输入:{1,2,3},{3,3,3}
输出:{1,2,3,3,3,3}
代码:归并
public class Solution {
public ListNode Merge(ListNode list1,ListNode list2) {
ListNode p = new ListNode(-1);
ListNode temp = p;
while(list1!=null && list2 !=null) {
if(list1.val <= list2.val) {
p.next = list1;
list1 = list1.next;
}else {
p.next = list2;
list2 = list2.next;
}
p=p.next;
}
if(list1!=null) {
p.next = list1;
}
if(list2!= null) {
p.next = list2;
}
return temp.next;
}
}
5. 合并k个已排序的链表
合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。
要求:时间复杂度 O(nlogn)
示例:
输入:[{1,2,3},{4,5,6,7}]
返回值:{1,2,3,4,5,6,7}
代码:
归并排序+merge
import java.util.ArrayList;
public class Solution {
public ListNode mergeKLists(ArrayList<ListNode> lists) {
if(lists.size() == 0 ) return null;
if(lists.size() == 1) return lists.get(0);
return mergeHelp(lists, 0, lists.size()-1);
}
public ListNode mergeHelp(ArrayList<ListNode> lists, int start, int end) {
if(start > end) return null;
if(start == end) return lists.get(start);
ListNode left = mergeHelp(lists, start, (start+end)/2);
ListNode right = mergeHelp(lists, (start+end)/2+1, end);
return merge(left, right);
}
public ListNode merge(ListNode list1, ListNode list2) {
if(list1 == null) return list2;
if(list2 == null) return list1;
ListNode temp = new ListNode(-1);
ListNode p, q, head = temp;
while(list1 !=null && list2 !=null) {
p = list1.next;
q = list2.next;
if(list1.val <= list2.val) {
temp.next = list1;
list1 =p;
temp = temp.next;
}else {
temp.next = list2;
list2 = q;
temp = temp.next;
}
}
if(list1!=null) {
temp.next = list1;
}
if(list2!= null) {
temp.next = list2;
}
return head.next;
}
}
二、字符串
1. 验证IP地址
编写一个函数来验证输入的字符串是否是有效的 IPv4 或 IPv6 地址
IPv4 地址由十进制数和点来表示,每个地址包含4个十进制数,其范围为 0 - 255, 用(".")分割。比如,172.16.254.1;同时,IPv4 地址内的数不会以 0 开头。比如,地址 172.16.254.01 是不合法的。
IPv6 地址由8组16进制的数字来表示,每组表示 16 比特。这些组数字通过 (":")分割。比如, 2001:0db8:85a3:0000:0000:8a2e:0370:7334 是一个有效的地址。而且,我们可以加入一些以 0 开头的数字,字母可以使用大写,也可以是小写。所以,2001:db8:85a3:0:0:8A2E:0370:7334 也是一个有效的 IPv6 address地址 (即,忽略 0 开头,忽略大小写)。
然而,我们不能因为某个组的值为 0,而使用一个空的组,以至于出现 (:😃 的情况。 比如, 2001:0db8:85a3::8A2E:0370:7334 是无效的 IPv6 地址。
同时,在 IPv6 地址中,多余的 0 也是不被允许的。比如, 02001:0db8:85a3:0000:0000:8a2e:0370:7334 是无效的。
示例:
输入:"172.16.254.1"
返回值:"IPv4"
示例:
输入:"2001:0db8:85a3:0:0:8A2E:0370:7334"
返回值:"IPv6"
示例:
输入:"256.256.256.256"
返回值:"Neither"
代码:
public class Solution {
/**
* 验证IP地址
*
* @param IP string字符串 一个IP地址字符串
* @return string字符串
*/
public String solve(String IP) {
if (IP.contains(".")) {
if (!check4(IP)) return "Neither";
String[] i4s = IP.split("\\.");
if (i4s.length != 4) return "Neither";
for (int i = 0; i < 4; i++) {
if (i4s[i].length() == 0) return "Neither";
if (i4s[i].charAt(0) == '0') return "Neither";
if (Pattern.matches(".*[a-zA-Z]+.*", i4s[i])) return "Neither";
System.out.println(i4s[i] + " " + i4s[i].contains(".*[a-zA-Z]+.*"));
if (Integer.parseInt(i4s[i]) > 255 || Integer.parseInt(i4s[i]) < 0) return "Neither";
}
return "IPv4";
} else {
if (IP.contains("::")) return "Neither";
if (!check6(IP)) return "Neither";
String[] i6s = IP.split(":");
if (i6s.length != 8) return "Neither";
for (int i = 0; i < 8; i++) {
if (Pattern.matches(".*[g-zG-Z]+.*", i6s[i])) return "Neither";
if (i6s[i].length() > 4) return "Neither";
}
return "IPv6";
}
}
public boolean check4(String s) {
int sum = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '.') sum++;
}
return sum == 3;
}
public boolean check6(String s) {
int sum = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == ':') sum++;
}
return sum == 7;
}
}
三、贪心
1. 分糖果
一群孩子做游戏,现在请你根据游戏得分来发糖果,要求如下:
-
每个孩子不管得分多少,起码分到一个糖果。
-
任意两个相邻的孩子之间,得分较多的孩子必须拿多一些糖果。(若相同则无此限制,即可以等于1)
示例:
输入:[1,1,2]
返回值:4
说明:最优分配方案为1,1,2
示例:
输入:[1,2,3,3]
返回值:7
说明:最优分配方案为1,2,3,1
代码:
- 先从左往右遍历一遍,如果右边孩子的评分比左边的高,则右边孩子的糖果数更新为左边孩子的 糖果数加 1;
- 再从右往左遍历一遍,如果左边孩子的评分比右边的高,且左边孩子当前的糖果数不大于右边孩子的糖果数,则左边孩子的糖果数更新为右边孩子的糖+1
public class Solution {
public int candy (int[] arr) {
int[] sugger=new int[arr.length];
Arrays.fill(sugger, 1);
for(int i=1; i<arr.length; i++) {
if(arr[i]>arr[i-1]) {
sugger[i]=sugger[i-1]+1;
}
}
for(int i=arr.length-2; i>=0; i--) {
if(arr[i]>arr[i+1] && sugger[i]<=sugger[i+1]) {
sugger[i]=sugger[i+1]+1;
}
}
int sum=0;
for(int i=0; i<sugger.length; i++) {
sum+=sugger[i];
}
return sum;
}
}
2. 主持人调度
有 n 个活动即将举办,每个活动都有开始时间与活动的结束时间.一位活动主持人在同一时间只能参与一个活动。并且活动主持人需要全程参与活动。
求为了成功举办这 n 个活动,最少需要多少名主持人。
示例:
输入:4, [[1,2],[3,4],[3,5],[4,5]]
输出:2个
说明:[1,2][3,4],[4,5]一个,[3,5]一个
代码:贪心+堆
import java.util.*;
public class Solution {
public int minmumNumberOfHost (int n, int[][] startEnd) {
//排序,按开始时间从小到大,开始时间相同则按结束时间从小到大
Arrays.sort(startEnd, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if(o1[0]>=0 && o2[0]<0) return 1;
if(o1[0]<0 && o2[0]>=0) return -1;
if(o1[0] == o2[0]) {
if(o1[1]>=0 && o2[1]<0) return 1;
if(o1[1]<0 && o2[1]>=0) return -1;
return o1[1]-o2[1]; //返回正值,代表this(o1)比o2大,排到后面
}
return o1[0]-o2[0];
}
});
//存储结束时间的最小堆。查看堆顶(最小结束时间)是否<=当前活动的开始时间
//如果是,代表有空闲主持人可以用,并将堆顶换为当前活动的结束时间
PriorityQueue<Integer> queue =new PriorityQueue<>();
queue.add(startEnd[0][1]);
int start, end, temp;
for(int i=1; i<startEnd.length; i++) {
start = startEnd[i][0];
end = startEnd[i][1];
if(start >= queue.peek()) queue.poll();
queue.add(end);
}
return queue.size();
}
}
四、DFS
1. 没有重复项数字的全排列
给出一组数字,返回该组数字的所有排列
例如:
[1,2,3]的所有排列如下:
[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].
(以数字在数组中的位置靠前为优先级,按字典序排列输出)
代码:DFS
import java.util.*;
public class Solution {
ArrayList<ArrayList<Integer>> res;
ArrayList<Integer> level;
public void dfs(int[] num, int[] book) {
if(level.size()==num.length) {
res.add(new ArrayList<Integer>(level));
return;
}
for(int i =0; i<num.length; i++) {
if(book[i]==0) {
level.add(num[i]);
book[i]=1;
dfs(num, book);
level.remove(level.size()-1);
book[i]=0;
}
}
}
public ArrayList<ArrayList<Integer>> permute(int[] num) {
int[] book=new int[num.length];
res=new ArrayList<>();
level=new ArrayList<>();
dfs(num, book);
return res;
}
}
2. 有重复数字的全排列
给出一组可能包含重复项的数字,返回该组数字的所有排列。结果以字典序升序排列。
示例:
输入:[2,1,1]
返回值:[[1,1,2],[1,2,1],[2,1,1]]
代码:DFS
import java.util.*;
public class Solution {
ArrayList<ArrayList<Integer>> res;
ArrayList<Integer> level;
public void dfs(int[] num, int[] book) {
if (level.size() == num.length) {
res.add(new ArrayList<Integer>(level));
return;
}
for (int i = 0; i < num.length; i++) {
if (book[i] == 0) {
if (i > 0 && num[i] == num[i - 1] && book[i - 1] == 0) {
continue;
}
level.add(num[i]);
book[i] = 1;
dfs(num, book);
level.remove(level.size() - 1);
book[i] = 0;
}
}
}
public ArrayList<ArrayList<Integer>> permuteUnique(int[] num) {
int[] book = new int[num.length];
res = new ArrayList<>();
level = new ArrayList<>();
Arrays.sort(num);
dfs(num, book);
return res;
}
}
3. 字符串的排列
输入一个长度为 n 字符串,打印出该字符串中字符的所有排列,你可以以任意顺序返回这个字符串数组。
示例:
输入:"aab"
返回值:["aab","aba","baa"]
(不包含重复元素)
代码:DFS
public class Solution {
ArrayList<String> res;
ArrayList<Character> level;
public void dfs(char[] num, int[] book) {
if (level.size() == num.length) {
StringBuilder sb=new StringBuilder();
for (Character character : level) {
sb.append(character);
}
res.add(sb.toString());
return;
}
for (int i = 0; i < num.length; i++) {
if (book[i] == 0) {
if (i > 0 && num[i] == num[i - 1] && book[i - 1] == 0) {
continue;
}
level.add(num[i]);
book[i] = 1;
dfs(num, book);
level.remove(level.size() - 1);
book[i] = 0;
}
}
}
public ArrayList<String> Permutation(String str) {
char[] num=str.toCharArray();
int[] book = new int[num.length];
res = new ArrayList<>();
level = new ArrayList<>();
Arrays.sort(num);
dfs(num, book);
return res;
}
}
4.岛屿数量
给一个01矩阵,1代表是陆地,0代表海洋。
岛屿: 相邻陆地可以组成一个岛屿(相邻:上下左右),判断岛屿个数。
示例:
输入:
[
[1,1,0,0,0],
[0,1,0,1,1],
[0,0,0,1,1],
[0,0,0,0,0],
[0,0,1,1,1]
]
返回值:3
代码:DFS
import java.util.*;
public class Solution {
int[][] dp;
int[][] nag = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public void dfs(int x, int y, char[][] grid) {
dp[x][y] = 1;
int newx, newy;
for (int i = 0; i < 4; i++) {
newx = x + nag[i][0];
newy = y + nag[i][1];
if (newx >= 0 && newx < grid.length && newy >= 0 && newy < grid[0].length &&
grid[newx][newy] == '1' && dp[newx][newy] == 0) {
dfs(newx, newy, grid);
}
}
}
public int solve (char[][] grid) {
int sum = 0;
dp = new int[grid.length][grid[0].length];
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1' && dp[i][j] == 0) {
dfs(i, j, grid);
sum++;
}
}
}
return sum;
}
}
5. N皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。

示例:
输入:4
返回值:2
示例:
输入:8
返回值:92
代码:
public class Solution {
int sum;
int a[] = new int[10];
public void dfs(int k, int n) {
if (k == n) { sum++;
return; }
for (int i = 0; i < n; i++) { //遍历k行的n个位置
int j;
for (j = 0; j < k; j++) { //检查冲突
if (a[j] == i || Math.abs(a[j] - i) == Math.abs(k - j)) {
break;
}
}
if (j == k) {
a[k] = i;
dfs(k + 1, n);
}
}
}
public int Nqueen(int n) {
sum = 0;
dfs(0, n);
System.out.println(Arrays.toString(a));
return sum;
}
}
五、BFS
六、树
1. 红黑树
红黑树的特点:
- 根节点是黑色
- 空叶子节点是黑色
- 红色节点的子节点是黑色
- 每个节点或红或黑
- 任一结点到每个空叶子节点经过相同数目的黑色结点。
红黑树能够以 O(log(n)) 的时间复杂度进行搜索、插入、删除操作。 并且红黑树不像AVL树一样追求“完全平衡”,它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。

2. 拓扑排序
给定一个有向图,图节点的拓扑排序定义如下:
- 对于图中的每一条有向边
A -> B, 在拓扑排序中A一定在B之前. - 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
针对给定的有向图找到任意一种拓扑排序的顺序.
输入:
graph = {0,1,2,3#1,4#2,4,5#3,4,5#4#5}
输出:
[0, 1, 2, 3, 4, 5]
解释:
图如下所示:
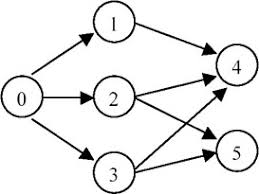
拓扑排序可以为:
[0, 1, 2, 3, 4, 5]
[0, 2, 3, 1, 5, 4]
...
您只需要返回给定图的任何一种拓扑顺序。
代码:
class DirectedGraphNode {
int label;
List<DirectedGraphNode> neighbors;
DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
public class Solution {
public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
Queue<DirectedGraphNode> queue=new ArrayDeque<>();
Map<DirectedGraphNode, Integer> map=new HashMap<>();
ArrayList<DirectedGraphNode> res=new ArrayList<>();
for(DirectedGraphNode node: graph)
{
map.putIfAbsent(node,0);
for(DirectedGraphNode neighbor: node.neighbors)
{
map.merge(neighbor, 1, Integer::sum);
}
}
map.forEach((k,v)->{
if(v==0) queue.add(k);
});
while (!queue.isEmpty())
{
DirectedGraphNode temp=queue.poll();
res.add(temp);
for(DirectedGraphNode neighbor: temp.neighbors)
{
map.put(neighbor, map.get(neighbor)-1);
if(map.get(neighbor)==0) queue.add(neighbor);
}
}
return res.size()==graph.size()?res:null;
}
}
七、动态规划
1. 组合方式4
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
示例:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
代码:
dp[i]: 代表target等于 i 时,由nums数组组合成 i 的个数
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1]; dp[0]=1;
for(int i=1; i<=target; i++) {
for(int j=0; j<nums.length; j++) {
if(i >= nums[j]) {
dp[i]+=dp[i-nums[j]];
}
}
}
return dp[target];
}
}
2. 粉刷房子
假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
costs[0][0] 表示第 0 号房子粉刷成红色的成本花费;costs[1][2] 表示第 1 号房子粉刷成绿色的花费,以此类推。
请计算出粉刷完所有房子最少的花费成本。
示例:
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色,1 号房子粉刷成绿色,2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。
代码:
dp[i] [j]代表:粉刷前i个房子,用j号颜色的最小花费
class Solution
{
public int minCost(int[][] costs) {
int n=costs.length, m=costs[0].length;
int dp[][]=new int[n+1][m];
for(int i=0;i<n;i++)
{
dp[i+1][0]=costs[i][0]+Math.min(dp[i][1], dp[i][2]);
dp[i+1][1]=costs[i][1]+Math.min(dp[i][0], dp[i][2]);
dp[i+1][2]=costs[i][2]+Math.min(dp[i][1], dp[i][0]);
}
return Math.min(dp[n][0], Math.min(dp[n][1], dp[n][2]));
}
}
3. 字符串解码方式
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> "1"
'B' -> "2"
...
'Z' -> "26"
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
"AAJF",将消息分组为(1 1 10 6)"KJF",将消息分组为(11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
示例:
输入:s = "12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
代码:
- ..13.. : dp[i] = dp[i-1]+dp[i-2], 0<= c[i-1], c[i] <= 26
- ..29.. : dp[i] = dp[i-1], c[i-1] [ci] >26
- ..10.. : dp[i] = dp[i-2], c[i]=0 && c[i-1]==1|| c[i-1] == 2
- ..00.. : dp[i] = 0, c[i] = 0 && (c[i-1]==0 || c[i-1]>3)
class Solution {
public int numDecodings(String s) {
int length=s.length();
char c[]=s.toCharArray();
int dp[]=new int[length+1];
dp[0]=1;
if(c[0]=='0') dp[1]=0;
else dp[1]=1;
for(int i=1;i<length;i++)
{
if(c[i]=='0')
{
if(c[i-1]=='0') dp[i+1]=0;
else dp[i+1]=dp[i-1];
}
else if(c[i-1]=='1'||(c[i-1]=='2'&&(c[i]>='0'&&c[i]<='6')))
dp[i+1]=dp[i]+dp[i-1];
else dp[i+1]=dp[i];
}
return dp[length];
}
}
4. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,2,1,1]
输出:3
代码:
class Solution {
public int longestConsecutive(int[] nums) {
if (nums.length == 0) return 0;
Arrays.sort(nums);
int[] dp = new int[nums.length];
dp[0] = 1;
int max = 1;
for (int i = 1; i < nums.length; i++) {
if (nums[i] - nums[i - 1] == 1) {
dp[i] = dp[i - 1] + 1;
} else if (nums[i] == nums[i - 1]) {
dp[i] = dp[i - 1];
} else dp[i] = 1;
max = Math.max(max, dp[i]);
}
return max;
}
}
5. 炸弹人
给定一个二维矩阵, 每一个格子可能是一堵墙 W,或者 一个敌人 E 或者空 0 (数字 '0'), 返回你可以用一个炸弹杀死的最大敌人数. 炸弹会杀死所有在同一行和同一列没有墙阻隔的敌人。 由于墙比较坚固,所以墙不会被摧毁.
示例:
输入:
grid =[
"0E00",
"E0WE",
"0E00"
]
输出: 3
解释:把炸弹放在 (1,1) 能杀3个敌人
代码:
dp[i] [j]: (i, j)的最大炸死敌人数
四个方向单独求,最后的结果是四个方向的总和。
public class Solution {
public int maxKilledEnemies(char[][] grid) {
int max=0, n=grid.length;
if(n==0) return max;
int m=grid[0].length;
int dp[]=new int[m+2];
int res[][]=new int[n][m];
//up
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
if(grid[i][j]=='W') dp[j+1]=0;
else if(grid[i][j]=='E') dp[j+1]+=1;
else res[i][j]+=dp[j+1];
}
Arrays.fill(dp, 0);
//left
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
if(grid[i][j]=='W') dp[j+1]=0;
else if(grid[i][j]=='E') dp[j+1]=dp[j]+1;
else { dp[j+1]=dp[j]; res[i][j]+=dp[j+1];}
}
Arrays.fill(dp, 0);
//down
for(int i=n-1;i>=0;i--)
for(int j=0;j<m;j++)
{
if(grid[i][j]=='W') dp[j+1]=0;
else if(grid[i][j]=='E') dp[j+1]+=1;
else { res[i][j]+=dp[j+1];}
}
Arrays.fill(dp, 0);
//right
for(int i=0;i<n;i++)
for(int j=m-1;j>=0;j--)
{
if(grid[i][j]=='W') dp[j+1]=0;
else if(grid[i][j]=='E') dp[j+1]=dp[j+2]+1;
else { dp[j+1]=dp[j+2]; res[i][j]+=dp[j+1]; max=Math.max(max, res[i][j]);}
}
return max;
}
}
6. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
代码:
class Solution {
public int rob(int[] nums) {
int dp[] = new int[nums.length + 1];
dp[0] = 0;
dp[1] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i + 1] = Math.max(dp[i], dp[i - 1] + nums[i]);
}
return dp[nums.length];
}
}
7. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
代码:
class Solution1 {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
int max = 1;
for (int i = 1; i < nums.length; i++) {
for (int j = i - 1; j >= 0; j--) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
max = Math.max(max, dp[i]);
}
return max;
}
}
8. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
代码:
class Solution {
public int numSquares(int n) {
int dp[] = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 1; i * i <= n; i++) {
for (int j = 1; j <= n; j++) {
dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
}
}
return dp[n];
}
}
9. 硬币排成线(博弈)
有 n 个硬币排成一条线。两个参赛者轮流从右边依次拿走 1 或 2 个硬币,直到没有硬币为止。拿到最后一枚硬币的人获胜。
请判定 先手玩家 必胜还是必败?
若必胜, 返回 true, 否则返回 false
示例:
输入: 4
输出: true
解释:
先手玩家第一轮拿走一个硬币, 此时还剩三个.
这时无论后手玩家拿一个还是两个, 下一次先手玩家都可以把剩下的硬币拿完.
代码:
递推式:dp[i] = !(dp[i-1] && dp[i-2])
public class Solution {
/**
* @param n: An integer
* @return: A boolean which equals to true if the first player will win
*/
public boolean firstWillWin(int n) {
if(n==0) return false;
if(n==1 || n==2) return true;
boolean dp[]=new boolean[n+1]; dp[1]=true; dp[2]=true;
for(int i=3;i<=n;i++)
dp[i]= !(dp[i-1]&&dp[i-2]);
return dp[n];
}
}
10. 硬币排成线II (博弈)
有 n 个不同价值的硬币排成一条线。两个参赛者轮流从 左边 依次拿走 1 或 2 个硬币,直到没有硬币为止。计算两个人分别拿到的硬币总价值,价值高的人获胜。
请判定 先手玩家 必胜还是必败?
若必胜, 返回 true, 否则返回 false.
示例:
输入: [1, 2, 2]
输出: true
解释: 先手玩家直接拿走两颗硬币即可.
代码:
public class Solution {
/**
* @param values: a vector of integers
* @return: a boolean which equals to true if the first player will win
*/
public boolean firstWillWin(int[] values) {
int n=values.length, sum=0;
if(n<=2) return true;
int dp[]=new int[n+1];
dp[n-1]=values[n-1];
dp[n-2]=values[n-1]+values[n-2];
dp[n-3]=values[n-3]+values[n-2];
for(int i=n-4;i>=0;i--)
{
dp[i]=Math.max(values[i]+Math.min(dp[i+2], dp[i+3]),
values[i]+values[i+1]+Math.min(dp[i+3], dp[i+4]));
sum+=values[i];
}
return dp[0]>(sum+values[n-1]+values[n-2]+values[n-3]-dp[0]);
}
}
11. 最长不连续回文子串
给一字符串 s, 找出在 s 中的最长回文子序列的长度. 你可以假设 s 的最大长度为 1000.
示例:
输入: "bbbab"
输出: 4
解释:
一个可能的最长回文序列为 "bbbb"
代码:
public class Solution {
public int longestPalindromeSubseq(String s) {
int n=s.length();
if(n==0) return 0;
int dp[][]=new int[n][n];
char c[]=s.toCharArray();
for(int i=n-1;i>=0;i--)
{
dp[i][i]=1;
for(int j=i+1;j<n;j++)
{
dp[i][j]=Math.max(dp[i+1][j], dp[i][j-1]);
if(c[i]==c[j]) dp[i][j]=Math.max(dp[i][j], dp[i+1][j-1]+2);
}
}
return dp[0][n-1];
}
}
12. 交叉字符串
给出三个字符串s1、s2、s3,判断s3是否由s1和s2交叉构成。
示例:
s1 = "aabcc"
s2 = "dbbca"
s3 = "aadbbcbcac"
代码:
dp[i][j]: s3[0, i+j]是否由s1[0, i]和s2[0, j]交叉构成
public class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int a=s1.length(), b=s2.length(), x=s3.length();
if((a+b)!=x) return false;
boolean dp[][]=new boolean[a+1][b+1];
char ca[]=s1.toCharArray(), cb[]=s2.toCharArray(), cx[]=s3.toCharArray();
dp[0][0]=true;
for(int i=0;i<=a;i++)
{
for(int j=0;j<=b;j++)
{
if(i==0&&j==0) continue;
if(i>0&&cx[i+j-1]==ca[i-1])
dp[i][j] |=dp[i-1][j];
if(j>0&&cx[i+j-1]==cb[j-1])
dp[i][j] |=dp[i][j-1];
}
}
return dp[a][b];
}
}
13. 不同子序列
给定字符串 S 和 T, 字符串S中有多少个子序列字符串和字符串T相同。
示例:
输入:S = "rabbbit",T = "rabbit"
输出:3
解释:你可以删除 S 中的任意一个 'b', 所以一共有 3 种方式得到 T.
示例:
输入:S = "abcd",T = ""
输出:1
解释:只有删除 S 中的所有字符这一种方式得到 T
代码:
public class Solution {
public int numDistinct(String S, String T) {
int n=T.length(), m=S.length();
int dp[][]=new int[n+1][m+1];
Arrays.fill(dp[0], 1);
char a[]=S.toCharArray();
char b[]=T.toCharArray();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=dp[i][j-1];
if(b[i-1]==a[j-1])
dp[i][j]+=dp[i-1][j-1];
}
}
return dp[n][m];
}
}


