分治法在二叉树的应用
分治法在二叉树的应用
二叉树
每个节点最多有两个子树的树结构。
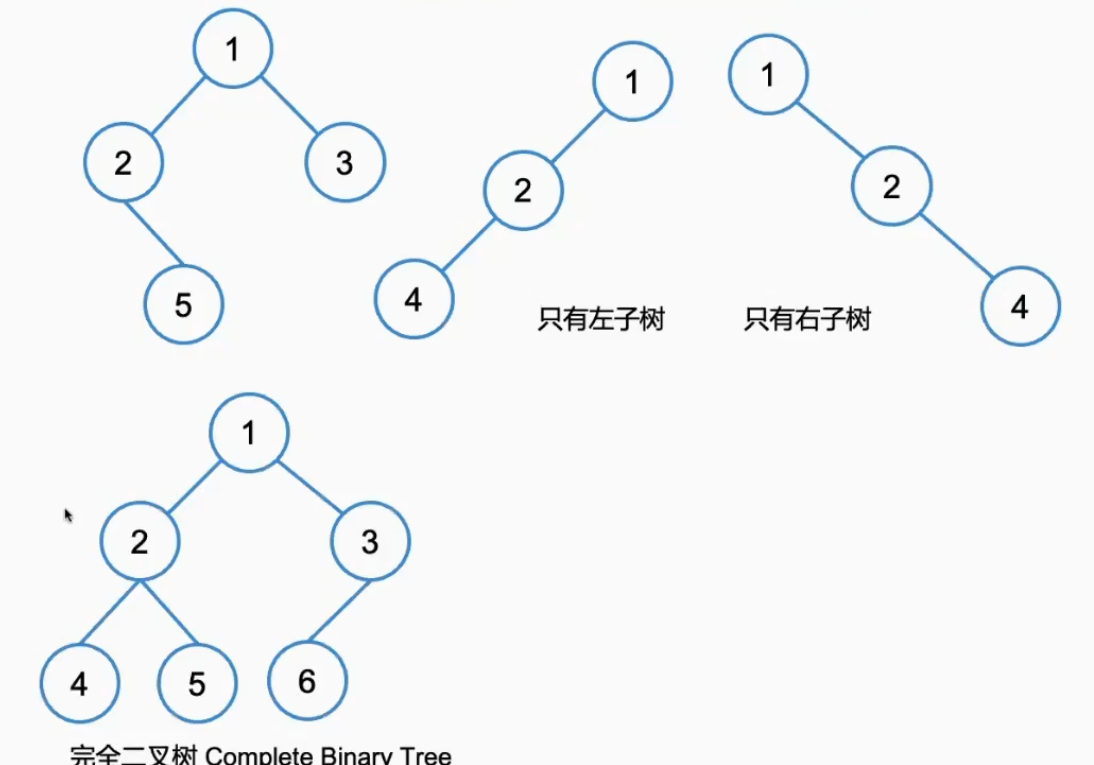
二叉树的高度:
O(logN)~O(N)之间
二叉树的时间复杂度:
时间复杂度:O(一次的复杂度)*次数
空间复杂度:O(一次的复杂度+深度)分治法
将问题分解为子问题求解,自己将子问题的结果进行合并,求出最终解。
二叉树中分治法的应用:
在二叉树中,考虑整棵树在该问题上的结果和左右子树在该问题上的结果之间的关系。
第一类:二叉树上的求值,求路径
第二类:二叉树结构变化
第三类:二叉查找树(Binary Search Tree)
左子树的值小于根节点的值,右子树的值大于根节点的值。
二叉平衡树(Balanced Binary Tree):
1.可以是一颗空树
2.左右子树的高度之差不大于1
3.子树也是一颗二叉平衡树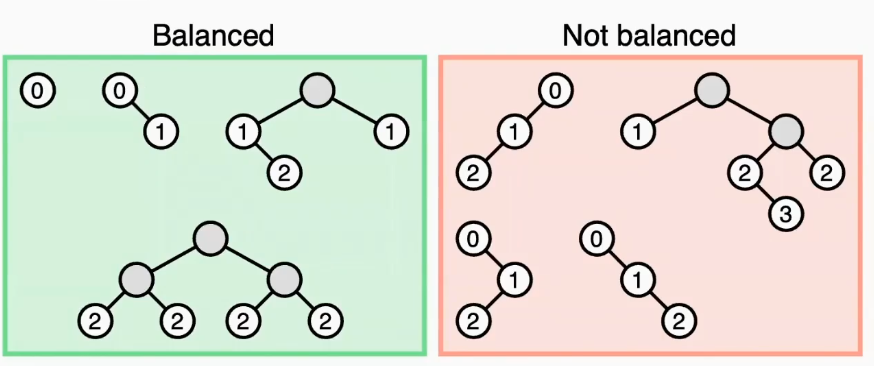
红黑树(Balanced BST)
Java中的TreeMap和TreeSet的数据结构就使用了红黑树
Java1.8中的HashMap的实现使用了TreeMap和LinkedList,使得在键冲突时快速查找键值。
效率:
O(logN)时间内实现增删改查
O(logN)时间内实现找最大最小值


