有向图中最大颜色值——1857

 

有向图中最大颜色值

题目：有向图中最大颜色值

给你一个 有向图 ，它含有 n 个节点和 m 条边。节点编号从 0 到 n - 1 。

给你一个字符串 colors ，其中 colors[i] 是小写英文字母，表示图中第 i 个节点的 颜色 （下标从 0 开始）。

给你一个二维数组 edges ，其中 edges[j] = [aj, bj] 表示从节点 aj 到节点 bj 有一条 有向边 。

图中一条有效 路径 是一个点序列 x1 -> x2 -> x3 -> ... -> xk。

返回给定图中有效路径里面的 最大颜色值。

提示：

n == colors.length
m == edges.length
1 <= n <= 105
0 <= m <= 105
colors 只含有小写英文字母。
0 <= aj, bj < n

 

示例1:

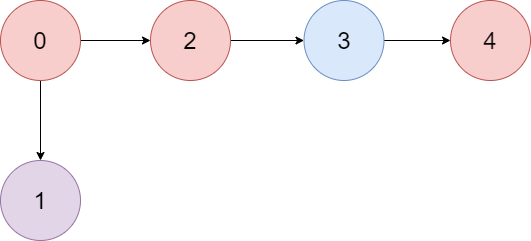
输入：colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
输出：3
解释：路径 0 -> 2 -> 3 -> 4 含有 3 个颜色为 "a" 的节点（上图中的红色节点）。

示例2：

输入：colors="hhqhuqhqff", edges=[[0,1],[0,2],[2,3],[3,4],[3,5],[5,6],[2,7],[6,7],[7,8],[3,8],[5,8],[8,9],[3,9],[6,9]]
输出：3

示例3：

输入：colors="nnllnzznn", edges=[[0,1],[1,2],[2,3],[2,4],[3,5],[4,6],[3,6],[5,6],[6,7],[7,8]]
输出：5

题解：拓扑排序+动态规划。

动态规划：dp[n][26]:遍历到n个节点时，26个颜色的最大值。

1. 根据图建立拓扑图。
2. 在拓扑排序中，节点出队列时，当前节点对应的颜色+1

   int temp = queue.poll();
   dp[temp][colors.charAt(temp) - 'a']++;

3. 遍历节点的连接点时，用当前节点的颜色更新连接点颜色的最大值。

   for (Integer next : map.get(temp)) {
        if (--indeg[next] == 0) {
            queue.add(next);
        }
        for (int i = 0; i < 26; i++) {
            dp[next][i] = Math.max(dp[next][i], dp[temp][i]);
        }
   }

Java代码：

class Solution {
        public int largestPathValue(String colors, int[][] edges) {
            Queue<Integer> queue = new ArrayDeque<>();
            Map<Integer, List<Integer>> map = new HashMap<>();
            int indeg[] = new int[colors.length()];
            int dp[][] = new int[colors.length()][26];

            //建立拓扑图
            for (int i = 0; i < edges.length; i++) {
                map.putIfAbsent(edges[i][0], new ArrayList<>());
                map.get(edges[i][0]).add(edges[i][1]);
                indeg[edges[i][1]]++;
            }

            //入度为0的点，入队列
            for (int i = 0; i < indeg.length; i++) {
                if (indeg[i] == 0) {
                    queue.add(i);
                }
            }

            //建立拓扑排序，并动态规划更新最大颜色值。
            int sum=0;
            while (!queue.isEmpty()) {
                int temp = queue.poll();
                dp[temp][colors.charAt(temp) - 'a']++;
                sum++;
                if (map.get(temp) != null) {
                    for (Integer next : map.get(temp)) {
                        if (--indeg[next] == 0) {
                            queue.add(next);
                        }
                        for (int i = 0; i < 26; i++) {
                            dp[next][i] = Math.max(dp[next][i], dp[temp][i]);
                        }
                    }
                }
            }

            if(sum!=colors.length())
                return -1;
            int max = 0;
            for (int i = 0; i < dp.length; i++) {
                for (int j = 0; j < 26; j++) {
                    max = Math.max(max, dp[i][j]);
                }
            }

            return max == 0 ? -1 : max;
        }
    }