在对数坐标系中绘制函数图象

本文记述了用 Matplotlib 在对数坐标系中绘制图象的一种方法，并在以 2 为底的对数坐标系上展示了 选择排序、冒泡排序（二）、快速排序（四） 的性能数据图象。

笔者按如下布局绘制了 12 (4x3)幅图象，其中 [a,b] 代表某幅图象的位置。

+---------------+---------------+---------------+
|               |               |               |
|    选择排序    |  冒泡排序（二）  |  快速排序（四） |
|               |               |               |      <-- X、Y 为普通坐标
|     [0,0]     |     [0,1]     |     [0,2]     |
|               |               |               |
+---------------+---------------+---------------+
|               |               |               |
|      "        |       "       |       "       |
|               |               |               |      <-- X、Y 轴同时应用对数坐标
|     [1,0]     |     [1,1]     |     [1,2]     |
|               |               |               |
+---------------+---------------+---------------+
|               |               |               |
|      "        |       "       |       "       |
|               |               |               |      <-- 仅 X 轴应用对数坐标
|     [2,0]     |     [2,1]     |     [2,2]     |
|               |               |               |
+---------------+---------------+---------------+
|               |               |               |
|       "       |       "       |       "       |
|               |               |               |      <-- 仅 Y 轴应用对数坐标
|     [3,0]     |     [3,1]     |     [3,2]     |
|               |               |               |
+---------------+---------------+---------------+

代码主体内容如下：

N = np.array([  1024,  2048,  4096,   8192,  16384,   32768,    65536,   131072 ])      #1
S = np.array([ 0.134, 0.537, 2.151,  8.599, 34.415, 137.924,  533.501, 2222.169 ])
B = np.array([ 0.300, 1.198, 4.777, 19.069, 76.458, 305.503, 1213.778, 4877.336 ])
Q = np.array([ 0.006, 0.014, 0.029,  0.061,  0.127,   0.271,    0.564,    1.196 ])

xfmtr = FuncFormatter(lambda x, pos: '{:1.0f}K'.format(x*1e-3) if x >= 1e3 else x)
yfmtr = FuncFormatter(lambda y, pos: '{:1.0f}K'.format(y*1e-3) if y >= 1e3 else y)

fig, axs = plt.subplots(4, 3, figsize=(12,9))           #2

axs[0,0].plot(N, S)                                     #3
axs[0,0].set(title='Selection\n Normal Scalar')
axs[0,0].set(xlabel='N', ylabel='Time')
axs[0,0].grid()
axs[0,0].xaxis.set_major_formatter(xfmtr)               #4
axs[0,0].yaxis.set_major_formatter(yfmtr)

...

axs[1,0].loglog(N, S, basex=2, basey=2)                 #5
axs[1,0].set(title='Log Scalar on X & Y')
axs[1,0].grid()
axs[1,0].xaxis.set_major_formatter(xfmtr)
axs[1,0].yaxis.set_major_formatter(yfmtr)

...

axs[2,0].semilogx(N, S, basex=2)                        #6
axs[2,0].set(title='Log Scalar on X')
axs[2,0].grid()
axs[2,0].xaxis.set_major_formatter(xfmtr)
axs[2,0].yaxis.set_major_formatter(yfmtr)

...

axs[3,0].semilogy(N, S, basey=2)                        #7
axs[3,0].set(title='Log Scalar on Y')
axs[3,0].grid()
axs[3,0].xaxis.set_major_formatter(xfmtr)
axs[3,0].yaxis.set_major_formatter(yfmtr)

...

plt.show()

首先将数据转换为 Numpy 的 ndarray（注：转化过程可省略）(#1)。准备 4x3 的绘图区域，每个绘图区域有独立的坐标系（#2）。在 [0,0] ~ [0,2] 位置，创建普通坐标系并绘制数据（#3），为了让坐标轴数据范围更清晰，同时简化了 X 和 Y 轴的主刻度值（#4）。在 [1,0] ~ [1,2] 位置，创建 X & Y 轴均以 2 为底的对数坐标系并绘制数据（#5）。在 [2,0] ~ [2,2] 位置，创建仅 X 轴以 2 为底的对数坐标系并绘制数据（#6）。在 [3,0] ~ [3,2] 位置，创建仅 Y 轴以 2 为底的对数坐标系并绘制数据（#7）。图象显示结果如下：

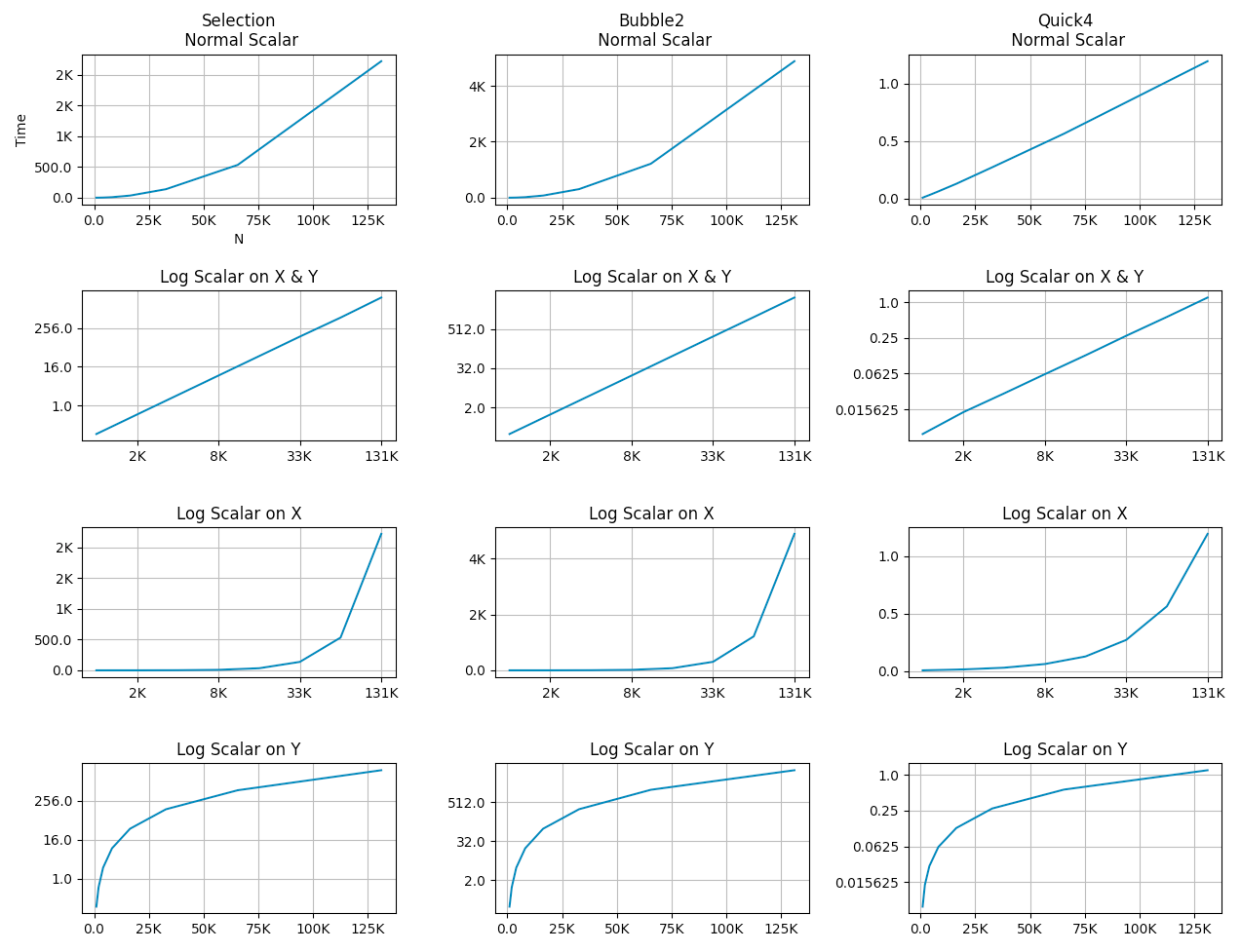
完整的代码请参考 [gitee] cnblogs/18388561 。

更多例子请参考 Matplotlib Gallery。