常见的排序算法——堆排序（六）

本文记述了堆排序算法改用多叉堆实现的基本思想和一份参考实现代码，并在说明了算法的性能后用随机数据进行了验证。

◆ 思想

多叉堆的完全树中，位置为 k 的节点，其父节点的位置为 ⎣(k + (d-2)) / d⎦，其子节点的位置为 k*d - (d-2)， k*d - (d-1), ..., k*d, k*d + 1。下沉操作中，在循环内用公式计算父子节点的位置关系。

◆ 实现

排序代码采用《算法（第4版）》的“排序算法类模板”实现。(代码中涉及的基础类，如 Array，请参考算法文章中涉及的若干基础类的主要API）

// heap6.hxx

...

template
<
    int _d              // #1
>
class Heap6
{

    ...
    
    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    void
    sort(Array<_T> & a)
    {
        int N = a.size();
        for (int k = (N+_d-2)/_d; k >= 1; --k)      // #2
            __sink__(a, k, N);
        while (N > 1) {
            __exch__(a, 1, N);              // #3
            --N;
            __sink__(a, 1, N);              // #4
        }
    }
    
    ...

    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    void
    __sink__(Array<_T> & a, int k, int n)
    {
        while (_d*k-(_d-2) <= n) {              // #5
            int j = _d*k-(_d-2);
            for (int i = j+1; i <= n && i <= _d*k+1; ++i)   // #6
                if (__less__(a[j-1], a[i-1])) j = i;
            if (!__less__(a[k-1], a[j-1])) break;
            __exch__(a, k, j);
            k = j;
        }
    }

    ...
    
    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    bool
    __less__(_T const& v, _T const& w)
    {
        return v.compare_to(w) < 0;         // #7
    }

    ...
    
    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    void
    __exch__(Array<_T> & a, int i, int j)
    {
        _T t = a[i-1];
        a[i-1] = a[j-1];
        a[j-1] = t;
    }

    ...

从外部指定多叉堆的叉数（#1）。从当前待排序范围 1/d 的位置开始向第一个位置扫描，用下沉操作达到堆有序的状态（#2）。将当前堆中的最大元素放到堆底的最后位置（#3）。然后对新的堆顶元素做下沉操作后，使新堆也恢复到堆有序状态（#4）。该算法用的是多叉堆（#5），所以某个节点与其 d 个子节点都比较后，决定是否继续下沉（#6）。将 '<' 改为 '>'，即得到逆序的结果（#7）。

◆ 性能

时间复杂度	空间复杂度	是否稳定
N*log(N)	1	否

◆ 验证

测试代码采用《算法（第4版）》的倍率实验方案，用随机数据验证其正确性并获取时间复杂度数据。

// test.cpp
    
...

time_trial(int N)
{
    Array<double> time(7);  // time[0..1] are NOT used.

    Array<Double> x(N);
    for (int i = 0; i < N; ++i) x[i] = Std_Random::random();    // #1

    Array<Double> a(N);
    for (int i = 0; i < N; ++i) a[i] = x[i];
    Stopwatch timer2;
    Heap6<2>::sort(a);                                   // #2
    time[2] = timer2.elapsed_time();
    assert(Heap6<2>::is_sorted(a));                      // #3
    a.~Array();

    Array<Double> b(N);
    for (int i = 0; i < N; ++i) b[i] = x[i];
    Stopwatch timer3;
    Heap6<3>::sort(b);
    time[3] = timer3.elapsed_time();
    assert(Heap6<3>::is_sorted(b));
    b.~Array();
    
    ...
    
    return time;
}

...

test(char * argv[])
{
    int T = std::stoi(argv[1]);          // #4
    Array<double> prev = time_trial(512);
    Std_Out::printf("%10s%14s%7s%14s%7s%14s%7s%14s%7s%14s%7s\n", "N", "2-way Time", "Ratio", "3-way Time", "Ratio", "4-way Time", "Ratio", "5-way Time", "Ratio", "6-way Time", "Ratio");
    for (int i = 0, N = 1024; i < T; ++i, N += N) {            // #5
        Array<double> time = time_trial(N);
        Std_Out::printf("%10d%14.3f%7.2f%14.3f%7.2f%14.3f%7.2f%14.3f%7.2f%14.3f%7.2f\n", N, time[2], time[2]/prev[2], time[3], time[3]/prev[3], time[4], time[4]/prev[4], time[5], time[5]/prev[5], time[6], time[6]/prev[6]);          // #6
        prev = time;
    }
}

...

用 [0,1) 之间的实数初始化待排序数组（#1）。针对 2 叉堆排序，打开计时器后执行排序（#2），确保得到正确的排序结果（#3）。对于其它多叉堆，重复 2 叉堆排序相同的处理过程。整个测试过程要执行 T 次排序（#4）。每次执行排序的数据规模都会翻倍（#5），并以上一次排序的时间为基础计算倍率（#6），

此测试在实验环境一中完成，

$ g++ -std=c++11 test.cpp std_out.cpp std_random.cpp stopwatch.cpp type_wrappers.cpp

$ ./a.out 15

         N    2-way Time  Ratio    3-way Time  Ratio    4-way Time  Ratio    5-way Time  Ratio    6-way Time  Ratio
      1024         0.011   2.75         0.009   2.25         0.008   2.67         0.008   2.00         0.009   2.25
      2048         0.024   2.18         0.020   2.22         0.019   2.38         0.019   2.38         0.020   2.22
      4096         0.054   2.25         0.044   2.20         0.042   2.21         0.042   2.21         0.044   2.20
      8192         0.118   2.19         0.097   2.20         0.093   2.21         0.094   2.24         0.096   2.18
     16384         0.257   2.18         0.211   2.18         0.201   2.16         0.203   2.16         0.210   2.19
     32768         0.558   2.17         0.455   2.16         0.434   2.16         0.438   2.16         0.455   2.17
     65536         1.210   2.17         0.985   2.16         0.938   2.16         0.947   2.16         0.972   2.14
    131072         2.615   2.16         2.120   2.15         2.016   2.15         2.027   2.14         2.105   2.17
    262144         5.631   2.15         4.544   2.14         4.327   2.15         4.365   2.15         4.501   2.14
    524288        12.077   2.14         9.756   2.15         9.243   2.14         9.266   2.12         9.592   2.13
   1048576        25.804   2.14        21.058   2.16        20.044   2.17        20.171   2.18        20.847   2.17
   2097152        55.924   2.17        44.859   2.13        42.530   2.12        42.676   2.12        43.894   2.11
   4194304       118.701   2.12        95.167   2.12        88.814   2.09        88.772   2.08        91.656   2.09
   8388608       247.051   2.08       197.303   2.07       186.722   2.10       187.631   2.11       193.419   2.11
  16777216       523.097   2.12       417.181   2.11       394.029   2.11       394.554   2.10       406.248   2.10

可以看出，随着数据规模的成倍增长，各个多叉排序所花费的时间将是上一次规模的 2.1? 倍，且在不断地变小。对于随机数据而言，当 d = 4 或 5 时表现相当，且时间性能最佳。将数据反映到以 2 为底数的对数坐标系中，可以得到如下图像，

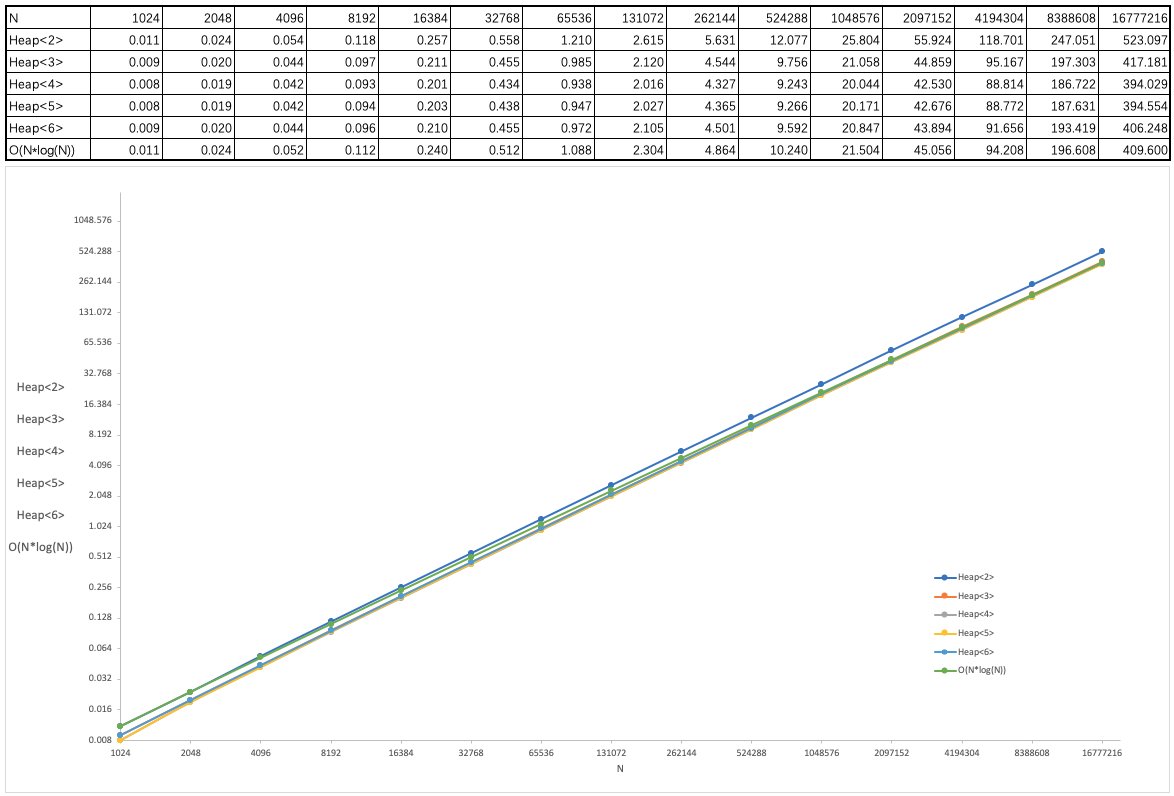
O(N*log(N)) 代表了线性对数级别复杂度下的理论排序时间，该行中的数据是以 Heap6<2> 行的第一个数据为基数逐一乘 2 + 2/log(N) 后得到的结果（因为做的是倍率实验，所以乘 (2*N*log(2*N)) / (N*log(N))，化简得到 2 + 2/log(N)，即乘 2+2/log(1024)，2+2/log(2048)，2+2/log(4096)，... 2+2/log(16777216)。因为是二叉堆，所以 log 的底数为 2）。

◆ 最后

完整的代码请参考 [gitee] cnblogs/18318363 。

查看性能对比，了解此算法与其它排序算法的相似性和差异性。

写作过程中，笔者参考了《算法（第4版）》的堆排序、练习题 2.4.41、“排序算法类模板”和倍率实验。致作者 Sedgwick，Wayne 及译者谢路云。