堆的基本概念、表示法和操作

本文记述了堆的基本概念、表示法和操作。

◆ 概念

堆是一种存放多个元素的数据结构，它要求每个元素都要大于等于或小于等于另外若干特定位置的元素。堆常用完全 d 叉树（以下简称“完全树”）表示，堆中的元素与树上的结点一一对应，这样的完全树是堆有序的，也被称为 d 叉堆。当完全树的每个结点都大于等于它的所有子结点时，称该堆为大根堆，反之则称为小根堆。

◆ 表示

堆通常用层次法来表示，还有前序法、后序法和中序法等。

层次法

把堆对应的完全树按照层级（从上到下，从左到右）的顺序放入数组中，规定根结点的逻辑位置为 1（若无特殊说明，位置指的是算法模型用的逻辑位置，而非内存存储用的物理位置）。

例如，含有 26 个元素的大根堆，

其完全二叉树的一种可能表示为，

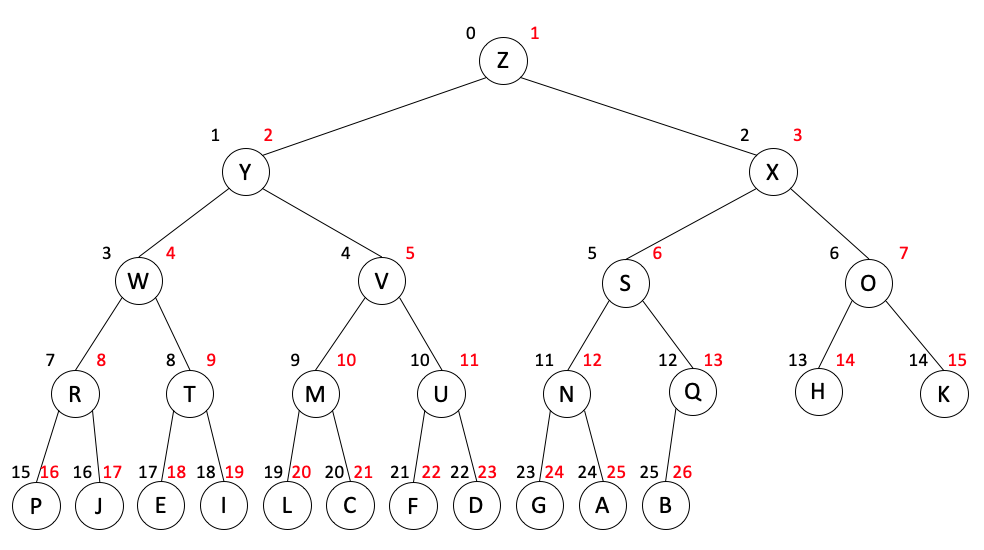
圆圈代表结点，结点左上方的黑色数字是其在内存存储中的物理位置，右上方的红色数字是其在算法模型中逻辑位置。下同。图中位置为 k 的结点，其父结点的位置为 ⎣k/2⎦，其子结点的位置为 2k 和 2k+1；

其完全三叉树的一种可能表示为，

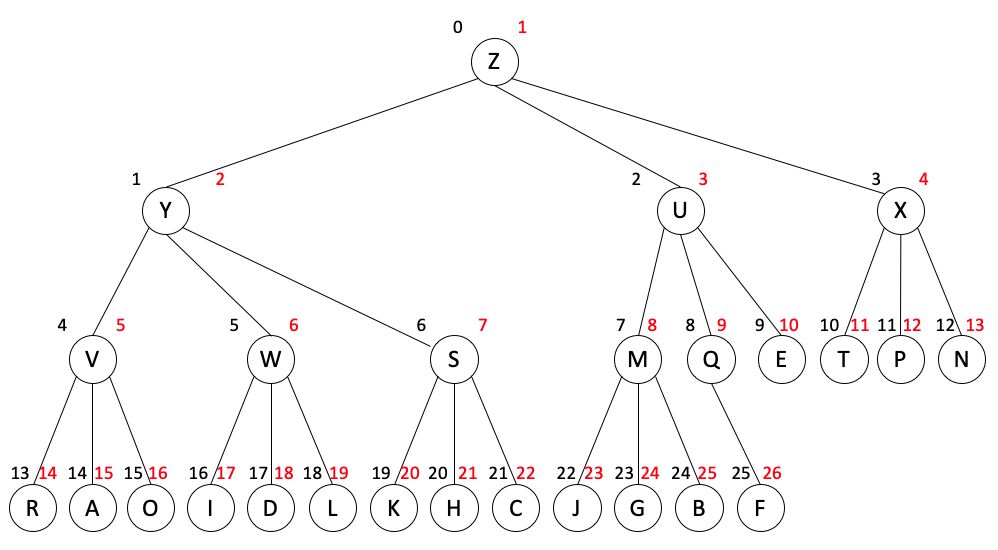
位置为 k 的结点，其父结点的位置为 ⎣(k+1)/3⎦，其子结点的位置为 3k-1，3k 和 3k+1；

其完全四叉树的一种可能表示为，

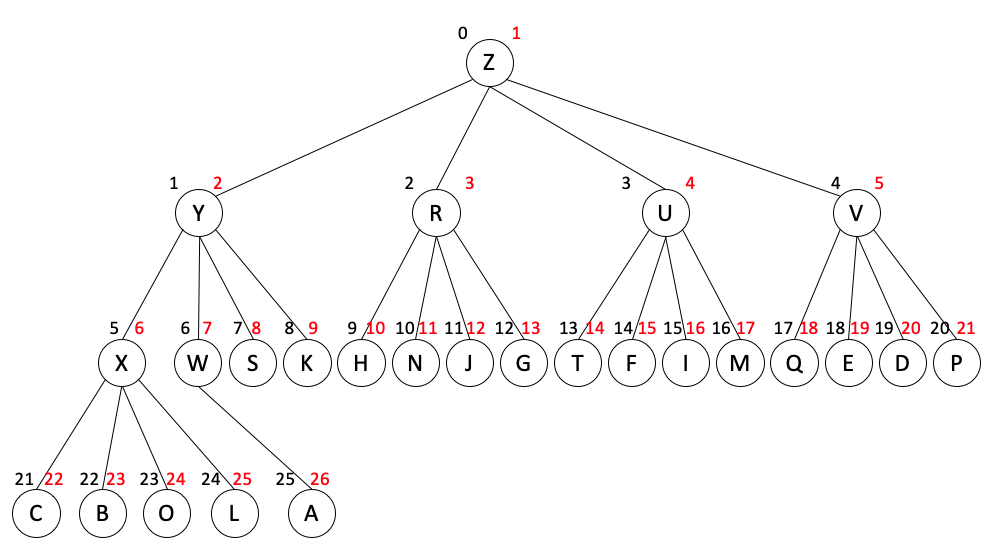
位置为 k 的结点，其父结点的位置为 ⎣(k+2)/4⎦，其子结点的位置为 4k-2，4k-1，4k 和 4k+1。

可以推导出，堆的完全 d 叉树中，位置为 k 的结点，其父结点的位置为 ⎣(k + (d-2)) / d⎦，其子结点的位置为 k*d - (d-2)， k*d - (d-1), ..., k*d, k*d + 1。

前序法

把堆对应的完全树按照前序遍历（先结点，再左子树，后右子树）的顺序放入数组中，规定根结点的逻辑位置为 1。例如，含有 26 个元素的大根堆，

其完全二叉树的一种可能表示为，

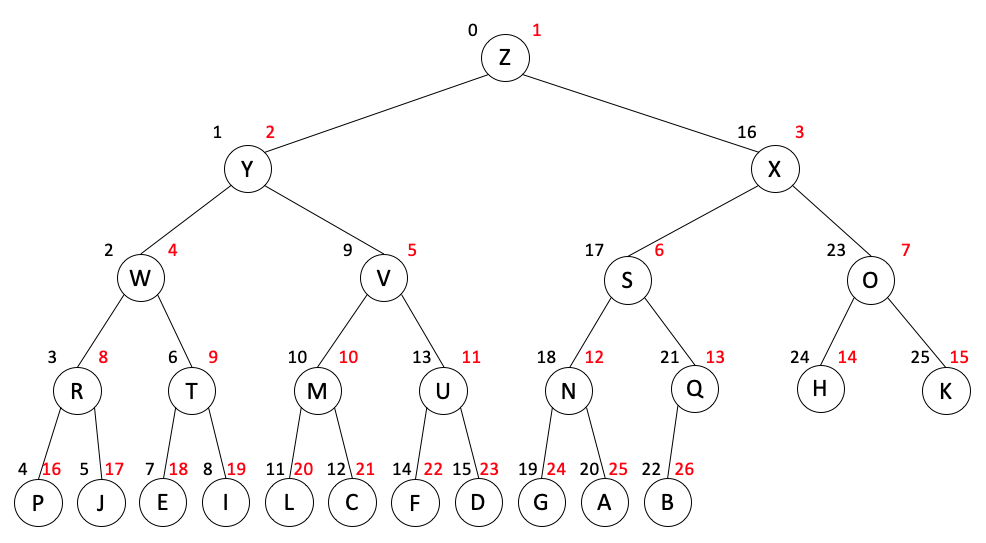
圆圈代表结点，结点左上方的黑色数字是其在内存存储中的物理位置，右上方的红色数字是其在算法模型中逻辑位置。下同。结点的位置需通过前序遍历生成。

其完全三叉树的一种可能表示为，

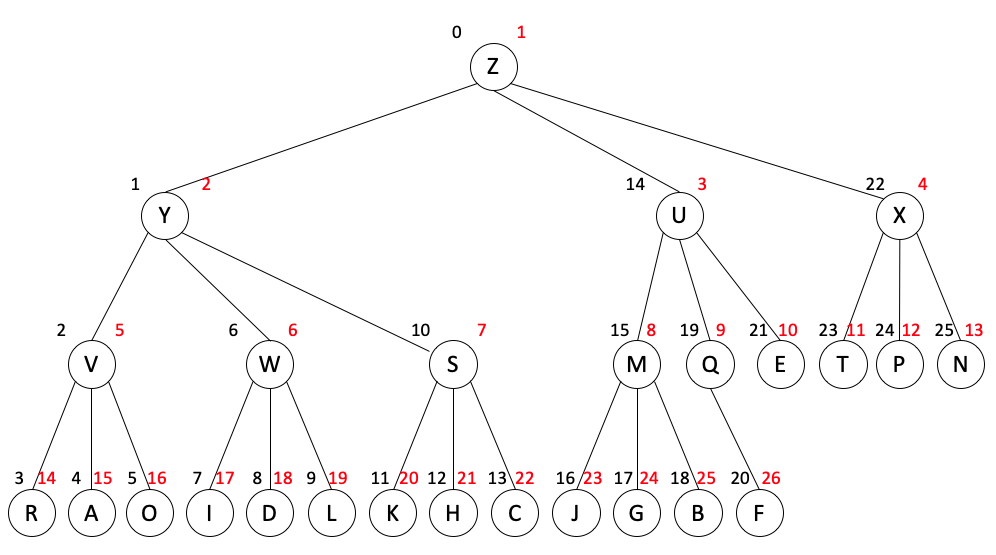
其完全四叉树的一种可能表示为，

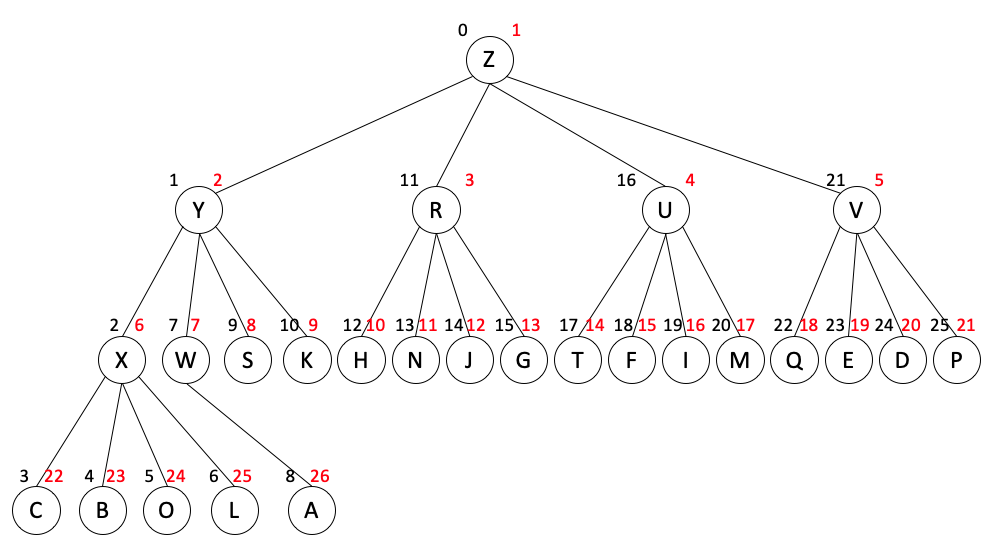
◆ 操作

堆需要保持有序的状态。在大根堆中，要保持父结点大于等于子结点；在小根堆中，要保持父结点小于等于子结点。为保持这种大小关系而进行的操作有上浮和下沉两种，统称为堆的有序化操作。

上浮操作是在完全树中自底向上地交换结点和其父结点来恢复堆的顺序，直到遇到了恰当的父结点（对于大根堆，就是找到更大的父结点；对于小根堆，就是找到更小的父结点）或到顶为止。

以前述三叉堆为例，堆中的 25 号结点 B，被替换为了 a，

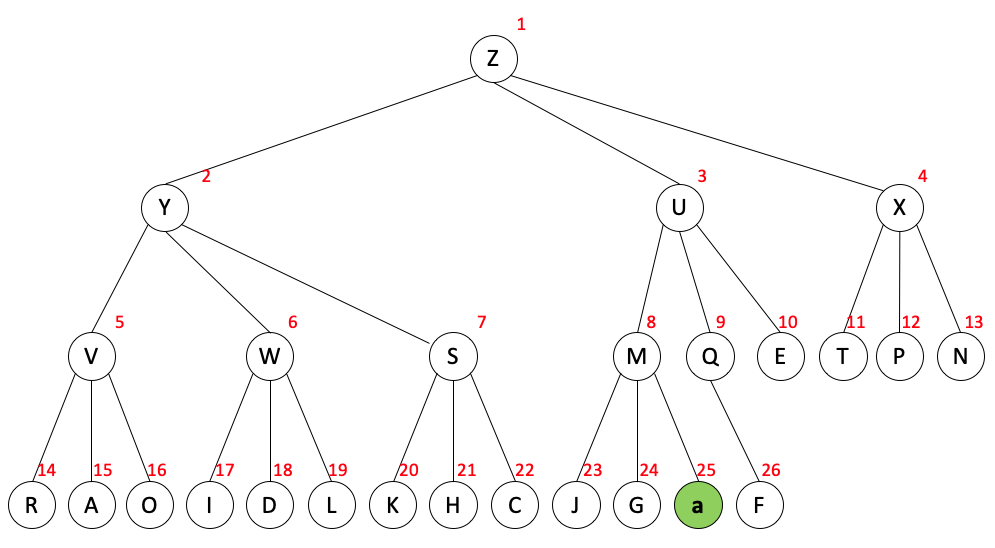
经过上浮操作后，堆变为了如下状态。

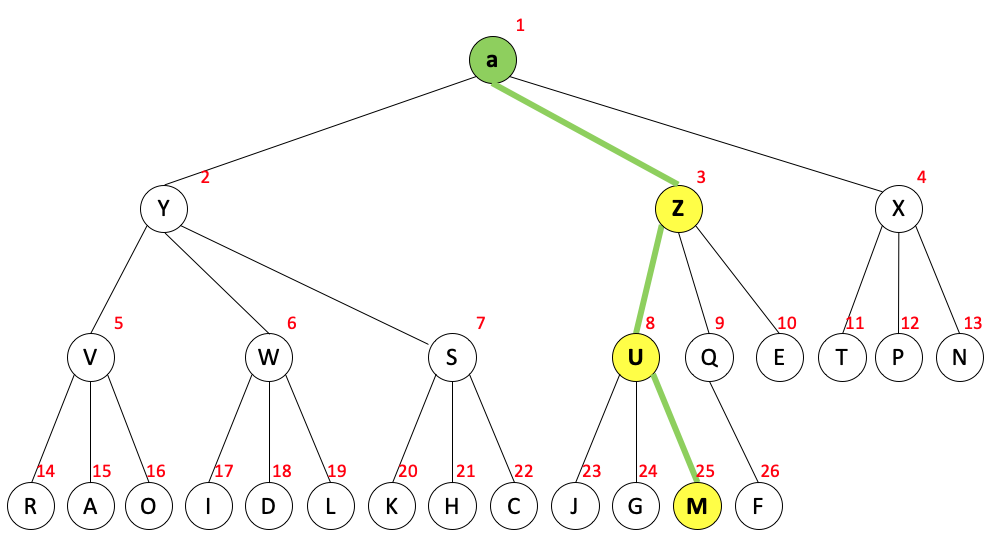
下沉操作是在完全树中自顶向下地交换结点和其较大子结点来恢复堆的顺序，直到遇到了恰当的子结点（对于大根堆，就是找到更小的子结点；对于小根堆，就是找到更大的子结点）或到底为止。

以前述三叉堆为例，堆中的 1 号结点 Z，被替换为了 @，

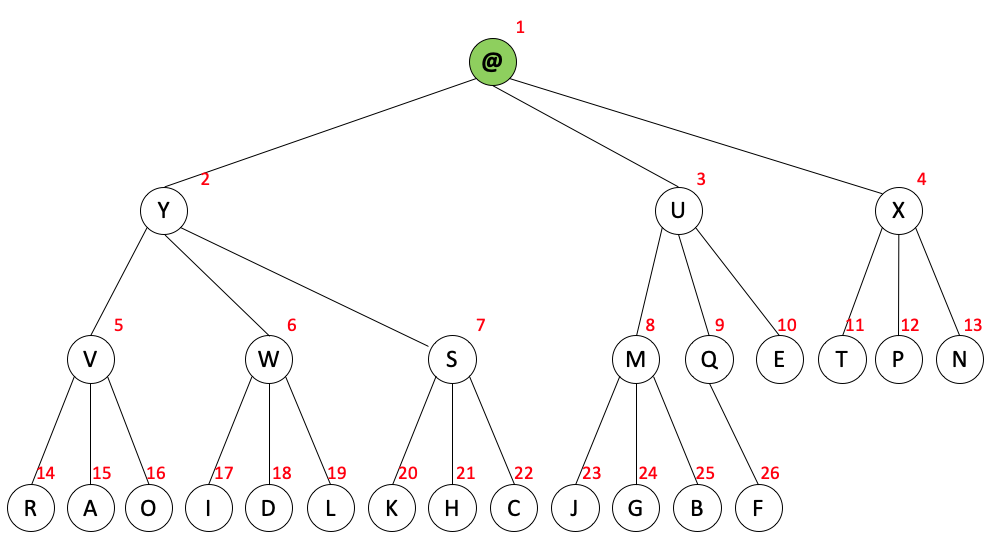
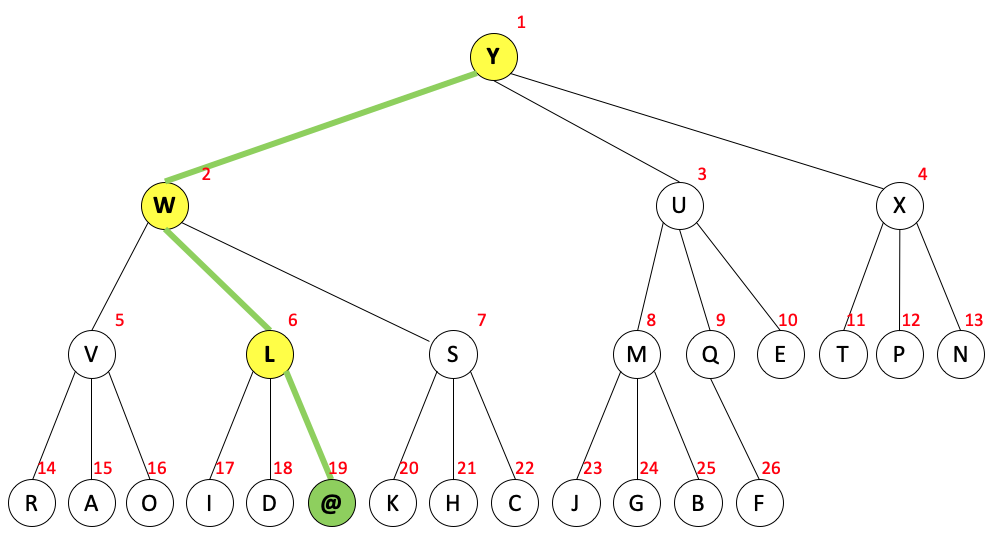
经过下沉操作后，堆变为了如下状态。